1, Linked list and adjacency list

1 linked list

   here, we do not use the commonly used structure plus pointer to realize the linked list, because in this way, each node should be new. The number of linked list nodes in common written test questions is 1e5~1e6 level, and new alone is enough to timeout.

  so we use arrays to simulate linked lists.

   the main purpose of single linked list is to realize the structure of adjacency table, which is often used to store graphs and trees.

I array analog single linked list

   e[N] to store the value of each node, and ne[N] to store the next pointer value of each node, as shown in the following example:

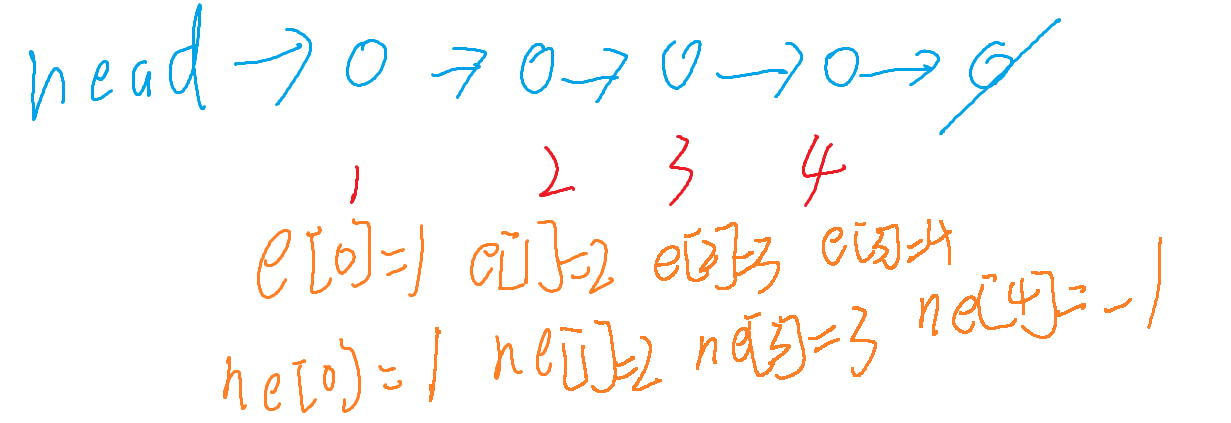
Example:

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
/*e[i]Store the value of node with subscript i ne[i] store the next pointer of node with subscript i*/
int e[N], ne[N];
/*head Stored is the subscript pointed to by the sentinel head node
idx Subscript indicating the next available node
*/
int head;
int idx;
//initialization
void Init()
{
    head = -1;
    idx = 0;
}
//Insert a node with the value of x after the head
void add_to_head(int x)
{
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx++;
}
//Insert a node with value x after the node with subscript k
void add(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx++;
}
// Delete the point after the point with subscript k
void remove(int k)
{
    /*Just point the next pointer of K to the next of ne[k]*/
    /*Directly when this point does not exist, do not worry about memory leakage in the algorithm problem*/
    ne[k] = ne[ne[k]];
}

int main()
{
    Init();
    int m;
    cin >> m;
    char op;
    int k, x;
    while (m--)
    {
        cin >> op;
        if (op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'D')
        {
            cin >> k;
            // If it is a head node, directly let the next of the head point to the ne of the node pointed to by the head, that is, head = ne[head];
            if (k == 0) head = ne[head];
            else
            {
                /*The subscript of the k-th insert is k - 1*/
                remove(k - 1);
            }
        }
        else
        {
            cin >> k >> x;
            add(k - 1, x);
        }
        //cout << op << ' ';
    }
    for (int i = head; i != -1; i = ne[i])
    {
        cout << e[i] << ' ';
    }
    return 0;
}

II array analog double linked list

  l[i] stores the subscript as the successor of node i, r[i] stores the subscript as the successor of node i, and e[i] stores the value of node I.

Example:

#include <iostream>
using namespace std;
const int N = 1e5 + 10;

int r[N];// Successor
int l[N];// Antecedent
int e[N];// value

int idx;//Next idle node

void Init()
{
    // Start with 0 as the head node
    // 1 ends as the right boundary
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}
// Insert a node with value x to the right of the node with subscript k
void add(int k, int x)
{
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx;
    idx++;
}
// Inserting to the left of K is equivalent to add(l[k], x)

// Delete points with subscript k
void remove(int k)
{
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

int main()
{
    Init();
    int m;
    cin >> m;
    char op1, op2;
    int k, x;
    while (m--)
    {
        cin >> op1;
        if (op1 == 'L')
        {
            cin >> x;
            add(0, x);
        }
        else if (op1 == 'R')
        {
            cin >> x;
            add(l[1], x);
        }
        else if (op1 == 'D')
        {
            cin >> k;
            // The subscript of the first inserted node is 2
            remove(k + 1);
        }
        else if (op1 == 'I')
        {
            cin >> op2;
            if (op2 == 'L')
            {
                cin >> k >> x;
                add(l[k + 1], x);
            }
            else
            {
                cin >> k >> x;
                add(k + 1, x);
            }
        }
    }
    for (int i = r[0]; i != 1; i = r[i])
    {
        cout << e[i] << ' ';
    }
    return 0;
}

   adjacency list is to open many single linked lists and put them together. It is equivalent to that every point connected with this point exists in this linked list. It is often used to store trees and graphs.

2, Stack and queue

  simulation stack:

#include <iostream>
#include <string>
using namespace std;

const int N = 1e5 + 10;
int Stack[N];
int top;

void Init()
{
    top = 0;
}

void Push(int x)
{
    Stack[top++] = x;
}

int Top()
{
    return Stack[top - 1];
}

bool empty()
{
    return top == 0;
}

void Pop()
{
    --top;
}

int main()
{
    int m;
    cin >> m;
    int x;
    string op;
    while (m--)
    {
        cin >> op;
        if (op == "push")
        {
            cin >> x;
            Push(x);
        }
        else if (op == "pop")
        {
            Pop();
        }
        else if (op == "empty")
        {
            if (empty()) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
        else
        {
            cout << Top() << endl;
        }
    }
    return 0;
}

Simulation queue:

#include <iostream>
#include <string>
using namespace std;

const int N = 1e5 + 10;
/*front Indicates the head of the queue. rear indicates the tail of the queue. If the tail of the queue is inserted out of the queue, then front++*/
int Queue[N];
int front;
int rear;

void Init()
{
    front = 0;
    rear = 0;
}

void Push(int x)
{
    Queue[rear++] = x;
}

void Pop()
{
    front++;
}

bool empty()
{
    return rear <= front;
}

int Front()
{
    return Queue[front];
}


int main()
{
    int m;
    cin >> m;
    string op;
    int x;
    while (m--)
    {
        cin >> op;
        if (op == "push")
        {
            cin >> x;
            Push(x);
        }
        else if (op == "pop")
        {
            Pop();
        }
        else if (op == "empty")
        {
            cout << (empty() ? "YES" : "NO") << endl;
        }
        else
        {
            cout << Front() << endl;
        }
    }
    return 0;
}

Monotone stack and monotone queue

I monotone stack

   model problem: given a sequence, find the number that is smaller (larger) than it on the left (right) side of each number.

   the consideration method is similar to the double pointer algorithm. First consider the violence algorithm, and then mine some properties to optimize the time complexity.

   the traditional violent method is to traverse each subscript forward, and the implicit points that can be optimized are shown in the figure:

   therefore, in the stack, if ax > = ay & & x < y, ax can be deleted, so the sequence in the stack must be a monotonic sequence.

code:

#include <iostream>
#include <stack>
using namespace std;


int main()
{
  /*A sequence of monotonically increasing elements is maintained in the stack
  Because if a [x] > = a [y] and x < y 
  Then either output a[y] or output the elements before a[y]. If a[y] does not meet the property, then
  a[y] >= a[i],Then a[x] must be > = a [i], so you can only output the elements in front of a[x]
  a[x]It's impossible to output*/
  stack<int> st;
  int n;
  cin >> n;
  int x;
  for (int i = 0; i < n; ++i)
  {
    cin >> x;
    while (!st.empty() && st.top() >= x)
    {
      st.pop();
    }
    if (st.empty()) cout << -1 << ' ';
    else cout << st.top() << ' ';
    st.push(x);
  }
  return 0;
}

  after replacing cin cout with scanf and printf, the speed is indeed improved:

   time complexity: for each element, it can be pushed in and out of the stack at most once, so the time complexity is O(n)

   some LeetCode examples of monotone stack:

// Solution 1
class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) 
    {
        stack<int> st;
        int n = nums.size();
        vector<int> ret(n, -1);
        /*Because it is a circular array, the module is elongated*/
        for (int i = 2 * n - 2; i >= 0; --i)
        {
            /*Walking backwards maintains a monotonically increasing stack of elements*/
            while (!st.empty() && st.top() <= nums[i % n]) st.pop();
            if (!st.empty()) ret[i % n] = st.top();
            st.push(nums[i % n]);
        }
        return ret;
    }
};

// Solution 2
class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) 
    {
        /*Monotone stack memory a set of increasing subscripts that have not yet been solved to calculate the next maximum element position
        For each element traversed, check whether the element value corresponding to the element at the top of the stack is less than the current element value
        If less than, let ret[st.top()] = nums[i] and pop to see the previous unsolved problem
        Otherwise, put the current element subscript i on the stack
        */
        int n = nums.size();
        vector<int> ret(n, -1);
        stack<int> st;
        for (int i = 0; i < 2 * n - 1 ; ++i)
        {
            while (!st.empty() && nums[st.top()] < nums[i % n])
            {
                ret[st.top()] = nums[i % n];
                st.pop();
            }
            st.push(i % n);
        }
        return ret;
    }
};

class Solution {
public:
    vector<int> nextLargerNodes(ListNode* head) 
    {
        auto cur = head;
        int n = 0;
        while (cur != nullptr)
        {
            cur = cur->next;
            ++n;
        }
        vector<int> ret(n, 0);
        /*A monotonically increasing subscript sequence is maintained in the stack, indicating that the subscript i corresponding to ret[i] is calculated*/
        stack<pair<int, int>> st;/*Node subscript element value to support random reading*/
        int curidx = 0;
        for (cur = head; cur != nullptr; cur = cur->next, ++curidx)
        {
            /*Similar to array monotone stack, can unresolved points in the stack be resolved through this point*/
            while (!st.empty() && st.top().second < cur->val)
            {
                ret[st.top().first] = cur->val;
                st.pop();
            }
            /*Then put the store in the stack*/
            st.push({curidx, cur->val});
        }
        return ret;
    }
};

II monotone queue

  the most classic application is to find the maximum and minimum values in the sliding window.

   monotone queue and monotone stack think in a similar way. First think about a violent approach, and then delete the useless elements to see if the queue is monotonous at this time.

   - 1 is the same.

   equal can be represented by the new equal number for output.

  therefore, the queue storing the minimum output value is a strictly monotonically increasing sequence.

code:

#include <iostream>
#include <deque>
using namespace std;

const int N = 1e6 + 10;

int main()
{
    int n, k;
    cin >> n >> k;
    int q[N];
    for (int i = 0; i < n; ++i) cin >> q[i];
    deque<int> dq1;// Monotonically increasing sequence used to output the minimum value element of the window
    deque<int> dq2;// Monotonically decreasing sequence used to output the maximum value element of the window
    for (int i = 0; i < n; ++i)
    {
        /*See if the team leader element is out of the window*/
        if (!dq1.empty() && dq1.front() < i - k + 1) dq1.pop_front();
        /*Monotonic increment of maintenance queue
        When outputting the minimum value, if the element at the end of the queue is greater than or equal to q[i] of this round in window 
        q[i]Yes, the last entry window exists for a longer time 
        There is no possibility of that big element output at all
        */
        /*Greater than or equal here can be replaced by greater than*/
        while (!dq1.empty() && q[dq1.back()] >= q[i]) dq1.pop_back();
        /*Save subscripts in the queue to see whether the first element of the queue is out of bounds*/
        dq1.push_back(i);
        if (i + 1 >= k)
        {
            printf("%d ", q[dq1.front()]);
        }
    }
    printf("\n");
    for (int i = 0; i < n; ++i)
    {
        /*See if the team leader element is out of the window*/
        if (!dq2.empty() && i - k + 1 > dq2.front()) dq2.pop_front();
        /*Monotonic decrement of maintenance queue
        When outputting the maximum value, if the element at the end of the queue is less than or equal to q[i] of this round in window 
        q[i]Yes, the last entry window exists for a longer time 
        There is no possibility of that small element output at all*/
        /*You can change less than or equal here*/
        while (!dq2.empty() && q[dq2.back()] <= q[i]) dq2.pop_back();
        dq2.push_back(i);
        if (i + 1 >= k)
        {
            printf("%d ", q[dq2.front()]);
        }
    }
    return 0;
}

   a better way to write after brushing the LeetCode question: when the element moved out of the window this time is the maximum or minimum value, it is necessary to let the head of the monotonous queue out of the queue.

#include <iostream>
#include <deque>
using namespace std;

const int N = 1e6 + 10;

int main()
{
  int n, k;
  cin >> n >> k;
  int q[N];
  for (int i = 0; i < n; ++i) cin >> q[i];
  deque<int> q1;
  deque<int> q2;
  for (int i = 0; i < n; ++i)
  {
    /*If the element to be removed is the queue head, let the queue head out of the queue*/
    if (!q1.empty() && i - k >= 0 && q1.front() == q[i - k]) q1.pop_front();
    /*When seeking the minimum value of the window, the elements that appear before me and are larger than me cannot be the minimum value*/
    /*Here is not the following standard to determine the exclusion of the team head element, so you can't change greater than or equal to here*/
    while (!q1.empty() && q1.back() > q[i]) q1.pop_back();
    q1.push_back(q[i]);
    if (i + 1 >= k)
    {
      cout << q1.front() << ' ';
    }
  }
  cout << endl;
  for (int i = 0; i < n; ++i)
  {
    /*If the element to be removed is the queue head, let the queue head out of the queue*/
    if (!q2.empty() && i - k >= 0 && q2.front() == q[i - k]) q2.pop_front();
    /*When calculating the maximum value of the window, the elements smaller than me can not be the maximum value*/
    /*Here is not the following standard to determine the exclusion of the team head element, so less than or equal to cannot be replaced here*/
    while (!q2.empty() && q2.back() < q[i]) q2.pop_back();
    q2.push_back(q[i]);
    if (i + 1 >= k) cout << q2.front() << ' ';
  }
  return 0;
}

  LeetCode monotone queue example:

class MaxQueue {
public:
    MaxQueue() 
    {
    }
    
    int max_value() 
    {
        if (q2.empty()) return -1;
        // Returns the first element of a monotonic queue q2
        return q2.front();
    }
    
    void push_back(int value) 
    {
        q1.push(value);
        // Elements smaller than value have no chance to output and maintain a monotonically decreasing (non strict) queue q2
        // The average time complexity of each element is O(1)
        while (!q2.empty() && q2.back() < value) q2.pop_back();
        q2.push_back(value);
    }
    
    int pop_front() 
    {
        if (q2.empty()) return -1;
        int val = q1.front();
        q1.pop();
        // If the ejected element is the largest element, you need to eject the first element of the two-way queue to keep it constant
        if (val == q2.front()) q2.pop_front();
        return val;
    }
private:
    queue<int> q1;// Used to store queue elements in response to pop_front
    deque<int> q2;// As a monotonically decreasing queue, the return max of O(1) is calculated_ value.
};

class Solution {
public:
    int longestSubarray(vector<int>& nums, int limit) 
    {
        int n = nums.size();
        int ret = 0;
        deque<int> q1;// Used to output the maximum monotonically decreasing sequence value, subscript
        deque<int> q2;// Monotonically increasing sequence value used to output the minimum value, subscript
        /*i Represents the leftmost position that can be reached by the subarray ending with j. it will not go to the left and is monotonous
        Double pointer algorithm can be used*/
        for (int j = 0, i = 0; j < n; ++j)
        {
            /*No element smaller than nums[j] can be the maximum*/
            while (!q1.empty() && q1.back() < nums[j]) q1.pop_back();
            /*Elements larger than nums[j] cannot be the minimum*/
            while (!q2.empty() && q2.back() > nums[j]) q2.pop_back();
            q1.push_back(nums[j]);
            q2.push_back(nums[j]);
            /*If the maximum minus minimum of the current interval [i,j] is greater than the limit, i will go forward and the maximum or minimum element may be removed*/
            while (!q1.empty() && !q2.empty() && q1.front() - q2.front() > limit)
            {
                /*If the currently removed element is equal to the queue head, the queue head will be removed*/
                if (nums[i] == q1.front()) q1.pop_front();
                if (nums[i] == q2.front()) q2.pop_front();
                i++;
            }
            ret = max(ret, j - i + 1);
        }
        return ret;
    }
};

3, KMP algorithm

                 81.

  violence is a two-tier cycle,

// Enumerating the starting point of a long string
for (int i = 1; i <= n; ++i)
{
    bool flag = true;
    for (int l = i, j = 1; j <= m, l <= n; ++j, ++l)
    {
        if (s[l] != p[j]) 
        {
            flag = false;
            break;
        }
    }
    if (flag == true)
    {
        break;
    }
}

  KMP's idea:

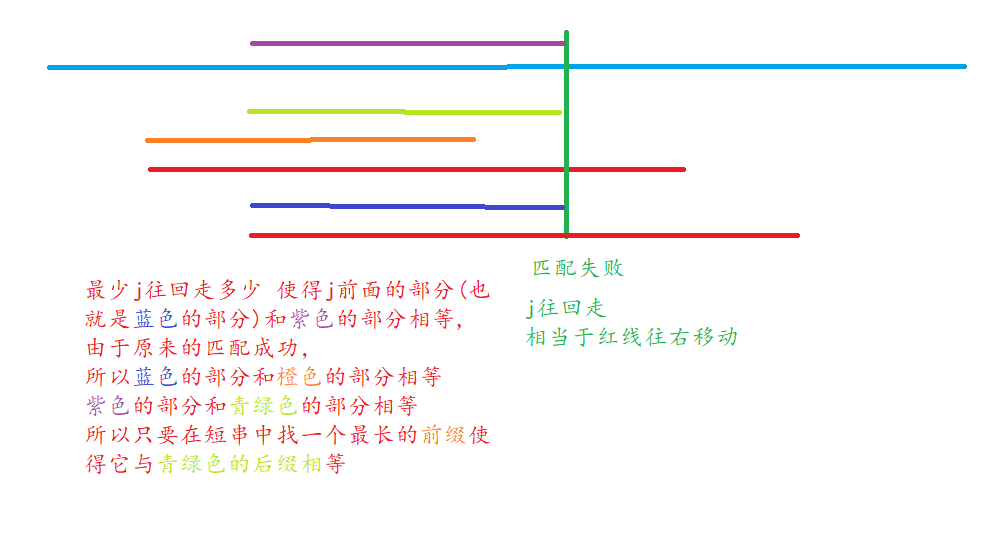
   this is the meaning of next[i]: the string ending with sub[i - 1] is equal to the string starting with sub[0], and the length of the string is the longest. At this time, the subscript of the next position at the end of the string starting with sub[0].

  specific code.

#include <iostream>
using namespace std;
const int N = 1e6 + 10;

char P[N];// Substring
char S[N];// Long string
int n, m;// Substring length long string length
int ne[N];// next array

int main()
{
    cin >> n >> P >> m >> S;
    ne[0] = -1;// 0 subscript matching failed, backtracking to - 1
    ne[1] = 0;// 1 subscript matching failed. It can only be traced back to 0
    int i = 2, k = 0;// Solve next[i] k save next[i - 1]
    // Solve ne array
    while (i < n)
    {
        /*P[i - 1]And P[k] are matching*/
        while (k != -1 && P[i - 1] != P[k]) k = ne[k];
        ne[i] = k + 1;
        ++i;
        ++k;
    }
    // matching
    i = 0;
    int j = 0;
    while (i < m)
    {
        /*S[i]And P[j] are matching*/
        while (j != -1 && S[i] != P[j]) j = ne[j];
        /*If you go here and match successfully or j goes to - 1, you can't match i 
        In short, at this time, i need to add 1 and j need to add 1*/
        ++i;
        ++j;
        /*If j goes to n, it means that P string matching is completed and returns once. The starting point at this time is i - j*/
        if (j == n)
        {
            cout << i - j << ' ';
            /*In order to find the successful location of the next matching completion
            We can see it as a failure of matching at P[n - 1]
            i was then equal to i - 1
            j To trace back to j = ne[n - 1]*/
            --i;
            j = ne[n - 1];
        }
    }
    return 0;
}

Save next[i - 1]
//Solve ne array
while (i < n)
{
/P[i - 1] and P[k] are matching/
while (k != -1 && P[i - 1] != P[k]) k = ne[k];
ne[i] = k + 1;
++i;
++k;
}
//Match
i = 0;
int j = 0;
while (i < m)
{
/S[i] and P[j] are matching/
while (j != -1 && S[i] != P[j]) j = ne[j];
/If you go here and match successfully or j goes to - 1, you can't match i
In short, at this time, i need to add 1 and j need to add 1/
++i;
++j;
/If j goes to n, it means that P string matching is completed and returns once. The starting point at this time is i - j/
if (j == n)
{
cout << i - j << ' ';
/In order to find the successful location of the next matching completion
We can see it as a failure of matching at P[n - 1]
i was then equal to i - 1
J goes back to j = ne[n - 1]/
–i;
j = ne[n - 1];
}
}
return 0;
}