Topology sort (TopSort)
August 5, 2021
1. Algorithm principle
1.1 one question
In daily life, some of our actions need to be in order. For example, you need to wear socks before shoes, pick up your watch before wearing it. The order cannot be changed.
Similarly, in a project, the work of each step needs to be in order, and the completion of some work is the precondition of others. We call each step of work an event.
Then, if the pre event of each event is known, how to determine its completion order?
We can build a network, place the pre event of each event before this event and connect it with directed segments, so we can intuitively see the sequence of events we need to complete.
The network built at this time is usually called activity on vertex network, or AOV network for short.
1.2 how to output sorting results by computer?
Topological sorting is a sort algorithm for this kind of problems.
After the above AOV network is established, we can record the nodes composed of each event.
First, add all nodes with a penetration of 0 to the queue (these events do not need pre events) and traverse their subsequent nodes. After traversing a node, the penetration of this node will be reduced by 1. When the penetration is reduced to 0, join the queue (pre events have been completed) and traverse its subsequent nodes.
After traversing all nodes, you can know their order.
1.3 diagram
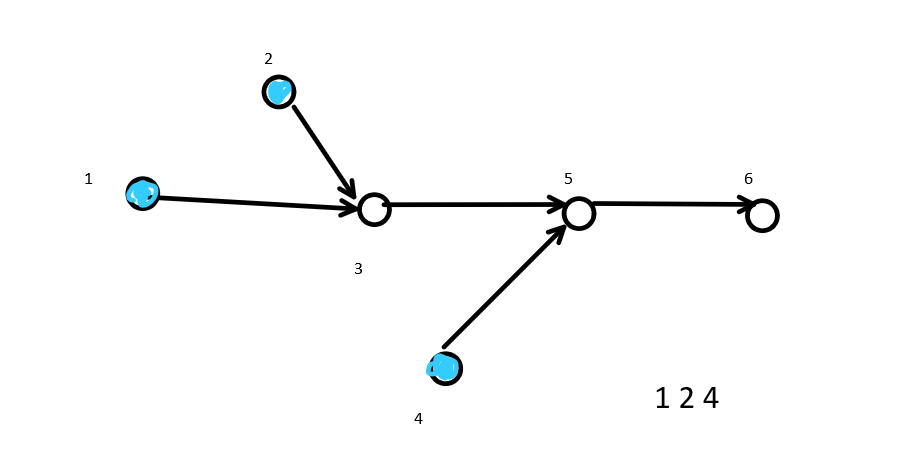
First, add nodes 1, 2 and 4 with a penetration of 0 to the queue, and first traverse the nodes after 1:
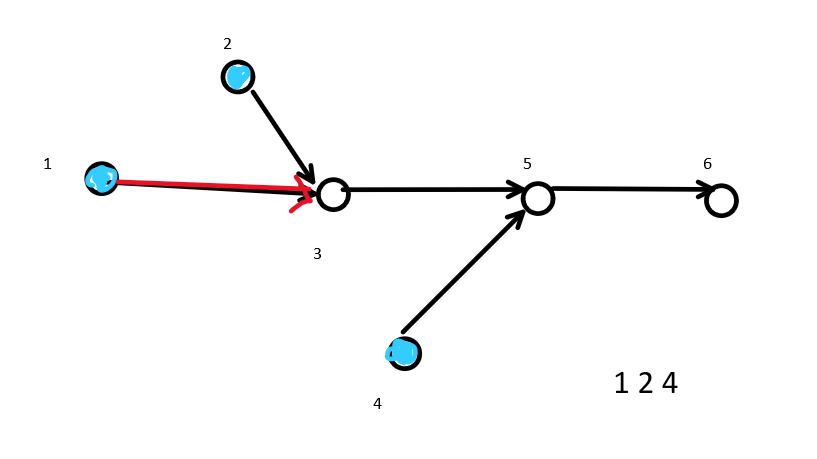
At this time, the penetration of node 3 minus 1 becomes 1, which is not equal to 0. Do not operate first, and then traverse the nodes after 2:
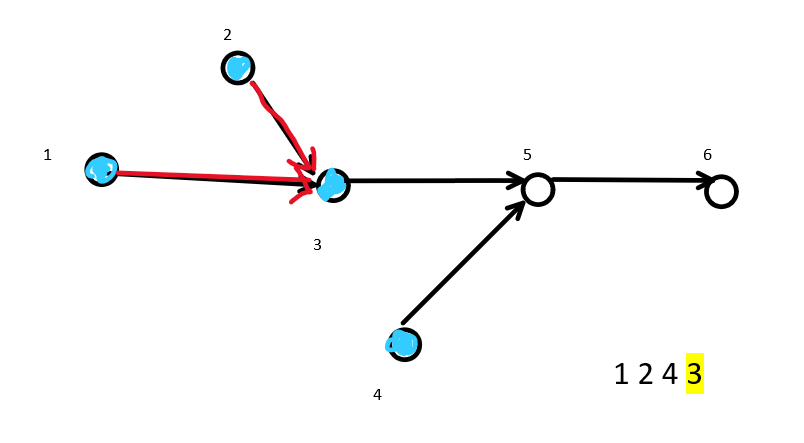
At this time, the penetration of node 3 is reduced to 0 and joins the queue.
Next, proceed as follows:
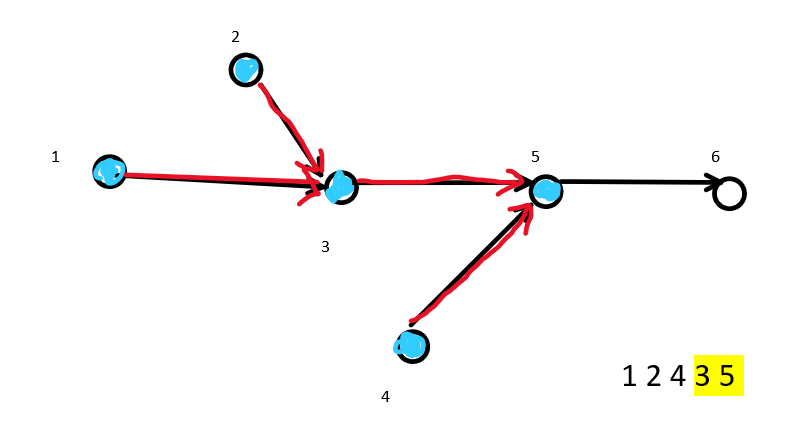
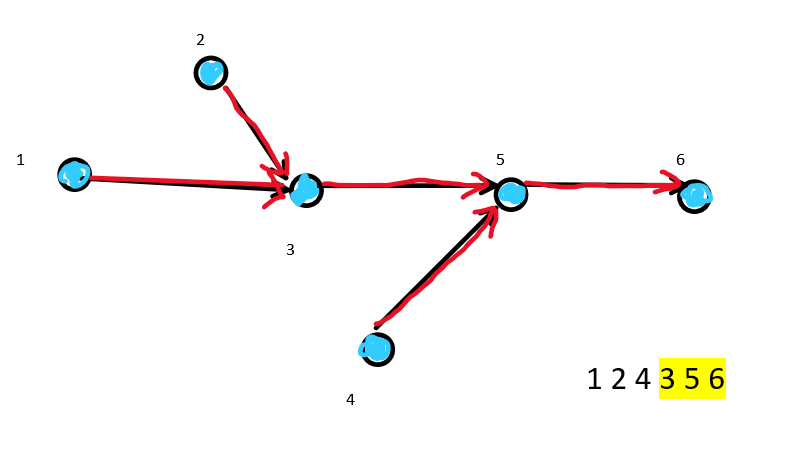
After traversing all nodes, the order is 1 2 4 3 5 6.
1.4 instability
Topological sorting is unstable when there are no other sorting conditions, which is related to the order and method you join the queue. For example, in the example shown above, it can also be written as 1 4 2 3 5 6, 4 1 2 3 5 6, etc.
In practical problems, the sequence of events in the same layer is irrelevant, so its correctness is not affected. If there are other requirements for sorting, you can join the queue in the required way.
1.5 unable to sort?
When the graph is a ring graph, it means that some nodes cannot reduce their penetration to 0, so it is impossible to sort their subsequent nodes, as shown in the figure:
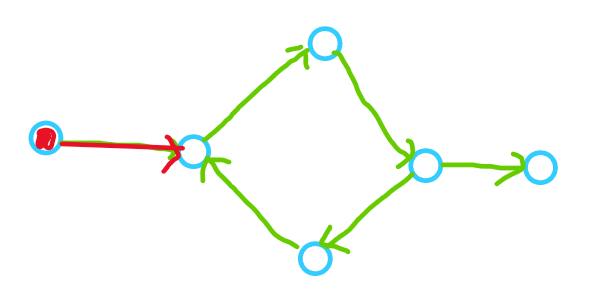
At this time, there are no points with a penetration of 0, so its order cannot be known.
Therefore, when sorting, we need to judge whether the number of all traversed points is equal to the number of all points. If not, it indicates that there is a ring and the sorting fails. If equal, the sorting succeeds.
1.6 time complexity
Because each node only needs to join the queue once, and each node needs to enter the queue several times before joining the queue, the time complexity is O(n+m).
2. Algorithm implementation
2.1 title
Give you n directed edges and m points. If topological sorting can be carried out, output the sorted sequence. If not, output - 1
The output is 1 line, and the answer may not be unique. Output any of the positive solutions.
2.2 solution analysis
First, record the penetration of all points. At this time, set the array (or other recording methods) inp [], add 1 to the penetration of the next event each time, and record the subsequent events of the previous event:
for(int i = 0; i < n; i++){
cin>>a>>b;
inp[b]++;
v[a].push_back(b);
}
Then, add each node with a penetration of 0 to the queue:
queue<int>q;
for (int i = 1; i <= m; i++) {//What is the starting point of the label
if (!inp[i])q.emplace(i);//0 to join the queue
}
Next, traverse the graph according to BFS:
while (!q.empty()) {
int fa = q.front();
q.pop();
pd++;//Record of points
ans[num++] = fa;//Recording sequence
for (auto now : v[fa]) {
inp[now]--;//Enter minus one
if (!inp[now]) {//0 to join the queue
q.emplace(now);
}
}
}
Finally, judge whether the sorting is successful:
if(pd==m)return 1; else return 0;
2.3 complete code
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<vector>
#include<queue>
using namespace std;
int inp[1005];
int n, m, pd;
vector<int>v[1005];
int ans[1005];
bool bfs() {
queue<int>q;
for (int i = 1; i <= m; i++) {
if (!inp[i])q.emplace(i);//0 to join the queue
}
while (!q.empty()) {
int fa = q.front();
q.pop();
ans[pd++] = fa;
for (auto now : v[fa]) {
inp[now]--;//Enter minus one
if (!inp[now]) {//0 to join the queue
q.emplace(now);
}
}
}
if (pd == m)return true;
else return false;
}
int main() {
int a, b;
cin >> n >> m;
for (int i = 0; i < n; i++) {
cin >> a >> b;
inp[b]++;
v[a].push_back(b);
}
if (bfs()) {
cout << ans[0];
for (int i = 1; i < m; i++){
cout << ' ' << ans[i];
}
}
else {
cout << -1;
}
cout << endl;
return 0;
}
Sample input 1:
5 6 1 3 2 3 3 5 4 5 5 6
Expected result 1:
1 2 4 3 5 6
Test result 1:
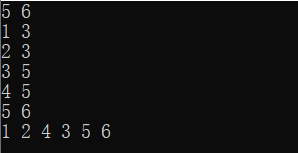
Sample input 2:
6 6 1 2 2 3 3 4 4 5 5 2 4 6
Expected result 2:
-1
Test result 2:

The above examples are passed.
Several examples
A: POJ - 2367 Genealogical tree
Description
The system of Martians' blood relations is confusing enough. Actually, Martians bud when they want and where they want. They gather together in different groups, so that a Martian can have one parent as well as ten. Nobody will be surprised by a hundred of children. Martians have got used to this and their style of life seems to them natural.
And in the Planetary Council the confusing genealogical system leads to some embarrassment. There meet the worthiest of Martians, and therefore in order to offend nobody in all of the discussions it is used first to give the floor to the old Martians, than to the younger ones and only than to the most young childless assessors. However, the maintenance of this order really is not a trivial task. Not always Martian knows all of his parents (and there's nothing to tell about his grandparents!). But if by a mistake first speak a grandson and only than his young appearing great-grandfather, this is a real scandal.
Your task is to write a program, which would define once and for all, an order that would guarantee that every member of the Council takes the floor earlier than each of his descendants.
Input
The first line of the standard input contains an only number N, 1 <= N <= 100 — a number of members of the Martian Planetary Council. According to the centuries-old tradition members of the Council are enumerated with the natural numbers from 1 up to N. Further, there are exactly N lines, moreover, the I-th line contains a list of I-th member's children. The list of children is a sequence of serial numbers of children in a arbitrary order separated by spaces. The list of children may be empty. The list (even if it is empty) ends with 0.
Output
The standard output should contain in its only line a sequence of speakers' numbers, separated by spaces. If several sequences satisfy the conditions of the problem, you are to write to the standard output any of them. At least one such sequence always exists.
Sample Input
5
0
4 5 1 0
1 0
5 3 0
3 0
Sample Output
2 4 5 3 1
analysis
In this question, enter the subsequent nodes of the ith node, and directly create a map and sort the topology.
code
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<vector>
#include<queue>
using namespace std;
int inp[1005], n, pd, num;
vector<int>v[1005];
int ans[1005];
bool bfs() {
queue<int>q;
for (int i = 1; i <= n; i++) {
if (!inp[i])q.emplace(i);//0 to join the queue
}
while (!q.empty()) {
int fa = q.front();
q.pop();
ans[pd++] = fa;
for(int i = 0; i < v[fa].size(); i++){
int now = v[fa][i];
inp[now]--;//Enter minus one
if (!inp[now]) {//0 to join the queue
q.emplace(now);
}
}
}
if (pd == n)return true;
else return false;
}
int main() {
int a;
cin >> n;
for (int i = 0; i < n; i++) {
while (cin >> a, a != 0) {
v[i + 1].push_back(a);
inp[a]++;
}
}
if (bfs()) {
cout << ans[0];
for (int i = 1; i < num; i++) {
cout << ' ' << ans[i];
}
}
else {
cout << -1;
}
cout << endl;
return 0;
}
B: HDU - 1285 Determine the competition ranking
Problem Description
There are N teams (1 < = N < = 500), the numbers are 1, 2, 3,..., N to compete. After the competition, the referee committee should rank all the participating teams from front to back, but now the referee committee can't directly obtain the competition results of each team. It only knows the results of each competition, that is, P1 wins P2, expressed by P1 and P2. When ranking, P1 precedes P2. Now please make a program to determine the ranking Name.
Input
There are several groups of inputs. The first row in each group has two numbers N (1 < = N < = 500), m; where N represents the number of teams, and M represents the input data of M rows. In the next M rows of data, each row also has two integers P1, and P2 represents that team P1 wins team P2.
Output
Give a ranking that meets the requirements. When outputting, there is a space between the team numbers, and there is no space after the last one.
Other notes: the qualified ranking may not be unique. At this time, the team with small number is required to be in the front when outputting; The input data is guaranteed to be correct, that is, the input data ensures that there must be a ranking that meets the requirements.
Sample Input
4 3
1 2
2 3
4 3
Sample Output
1 2 4 3
analysis:
This problem requires the team with small team number to be in the front, so you need to use the priority queue, and then build a map topology to sort.
code:
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<vector>
#include<queue>
#include<functional>
using namespace std;
int inp[505], n, m;
vector<int>v[505];
int ans[505];
void bfs() {
//queue<int>q;
int pd = 0;
priority_queue<int, vector<int>, greater<int>>q;//Due to the requirements of the topic, priority queue is used here
for (int i = 1; i <= n; i++) {
if (!inp[i])q.emplace(i);//0 to join the queue
}
while (!q.empty()) {
int fa = q.top();
q.pop();
ans[pd++] = fa;
for(int i = 0; i < v[fa].size(); i++){
int now = v[fa][i];
inp[now]--;//Enter minus one
if (!inp[now]) {//0 to join the queue
q.emplace(now);
}
}
}
}
int main() {
int a, b;
while (cin>>n>>m) {
memset(inp, 0, sizeof inp);
memset(v, 0, sizeof v);
for (int i = 0; i < m; i++) {
cin >> a >> b;
inp[b]++;
v[a].push_back(b);
}
bfs();
cout << ans[0];
for (int i = 1; i < n; i++) {
cout << ' ' << ans[i];
}
cout << '\n';
}
return 0;
}
C: HDU - 2094Produce champion
Problem Description
There are a group of people playing table tennis. They catch each other and kill each other. Each two people can play one game at most.
The rules of the game are as follows:
If A defeats B, B defeats C, and there is no competition between A and C, then it is determined that A can beat C.
If A defeats B, B defeats C, and C defeats A, then A, B and C cannot become champions.
According to this rule, the champion may be determined without circular competition. Your task is to face a group of competitors and determine whether you have actually produced a champion after several battles.
Input
The input contains some groups of players. Each group of players starts with an integer n (n < 1000), followed by the competition results of n pairs of players. The competition results are represented by the names of a pair of players (separated by a space), and the former defeats the latter. If n is 0, it means that the input is over.
Output
For each player group, if you judge that the production gives birth to the champion, output "Yes" in one line, otherwise output "No" in one line.
Sample Input
3
Alice Bob
Smith John
Alice Smith
5
a c
c d
d e
b e
a d
0
Sample Output
Yes
No
analysis:
This problem is to investigate the nature of topological sorting, that is, if there is only one champion, there is only one node with a degree of 0 in the initialization graph, so you can directly enumerate the number of nodes with a degree of 0.
code:
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string>
#include<map>
using namespace std;
map<string, int>mp;
bool solve(int n) {
int poc = 0;
for (auto x : mp) {
if (!x.second) {
poc++;
}
}
if (poc == 1)
return 1;
else
return 0;
}
int main() {
int n;
while (cin >> n, n != 0) {
mp.clear();
string k, l;
for (int i = 0; i < n; i++) {
cin >> k >> l;
mp[k] = mp[k];
mp[l]++;
}
if (solve(n))
cout << "Yes\n";
else
cout << "No\n";
}
return 0;
}