1, Basic problem solving skills of dynamic programming
Learning from: https://labuladong.gitee.io/algo/3/23/71/
1.1 change exchange (medium)
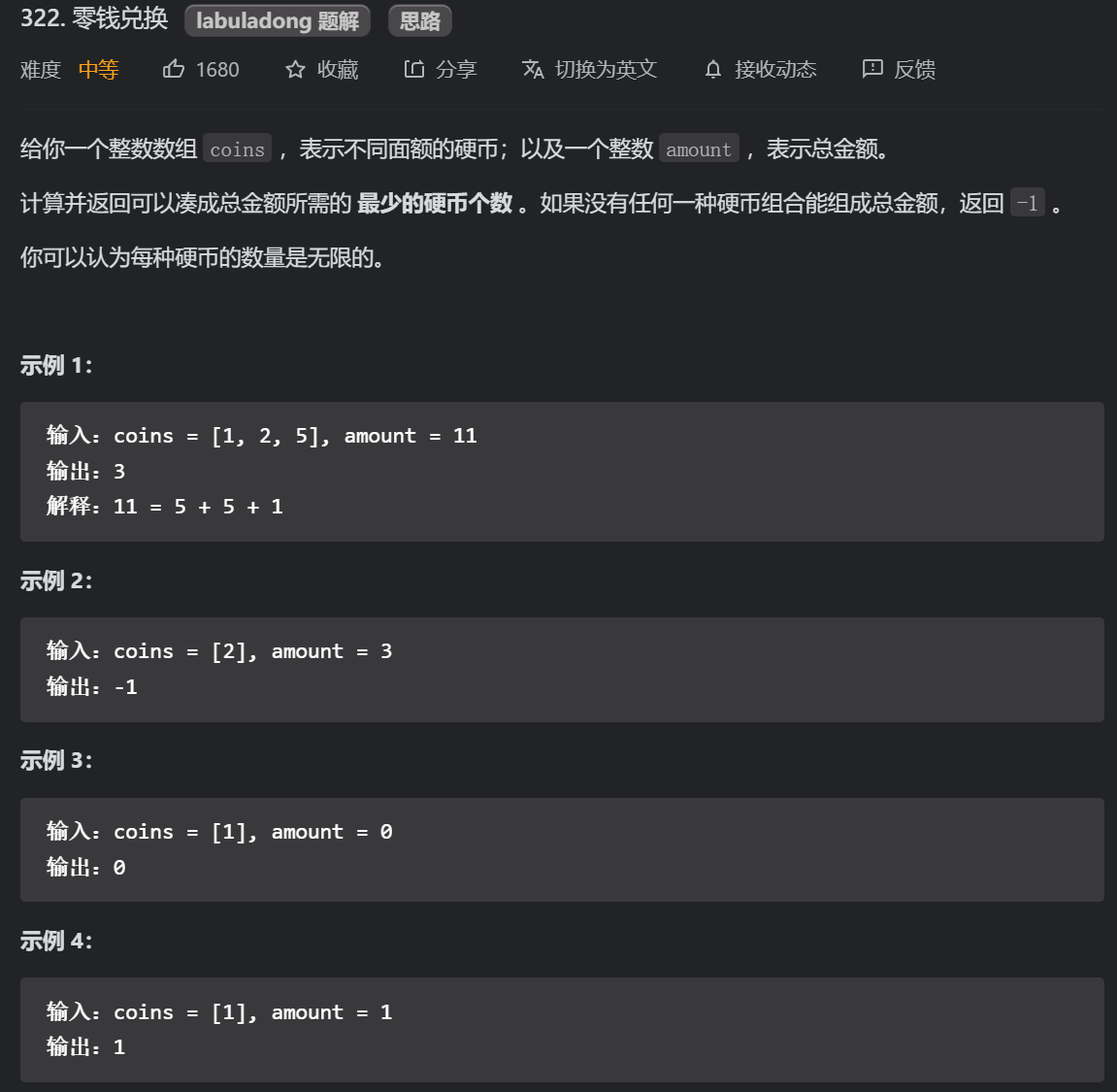

Make four points of analysis on the topic: base case, state (variables changed in the original problem and sub problem), selection (what causes the state to change), and the meaning of dp array
Back to this question, for a total amount m, the minimum number of coins it needs = min (M - the denomination of each coin) + 1. Of course, it should be judged that M - the denomination of each coin is greater than or equal to 0, otherwise skip.
Because the title says that coins are infinite, you need to traverse all coins in turn no matter what amount.
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// Because we are solving min, we must first set the initial dp array value to infinity
Arrays.fill(dp, amount + 1);
// It takes 0 coins to make 0 yuan
dp[0] = 0;
// Solve from amount 1 - amount in sequence
for (int i = 1; i <= amount; i++) {
// dp[i] = min(dp[i - coins[j] + 1]) (traverse all denominations coins[j])
for (int j = 0; j < coins.length; j++) {
// Judge whether the coin denomination exceeds the current amount
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
}
Isn't dynamic programming derived from the simplest base case? It can be imagined as a chain reaction, which is small and broad. However, only the problem conforming to the optimal substructure has the property of this chain reaction.
The process of finding the optimal substructure is actually the process of proving the correctness of the state transition equation. If the equation conforms to the optimal substructure, you can write the violent solution. If you write the violent solution, you can see whether there are overlapping subproblems. If there is any, it will be optimized and if there is no, it will be OK. This is also a routine. Friends who often brush questions should be able to understand it.
2, Subsequence type problem (array + string)
2.1 topics involving two strings and arrays
2.1.1 longest common subsequence (medium) (master template)
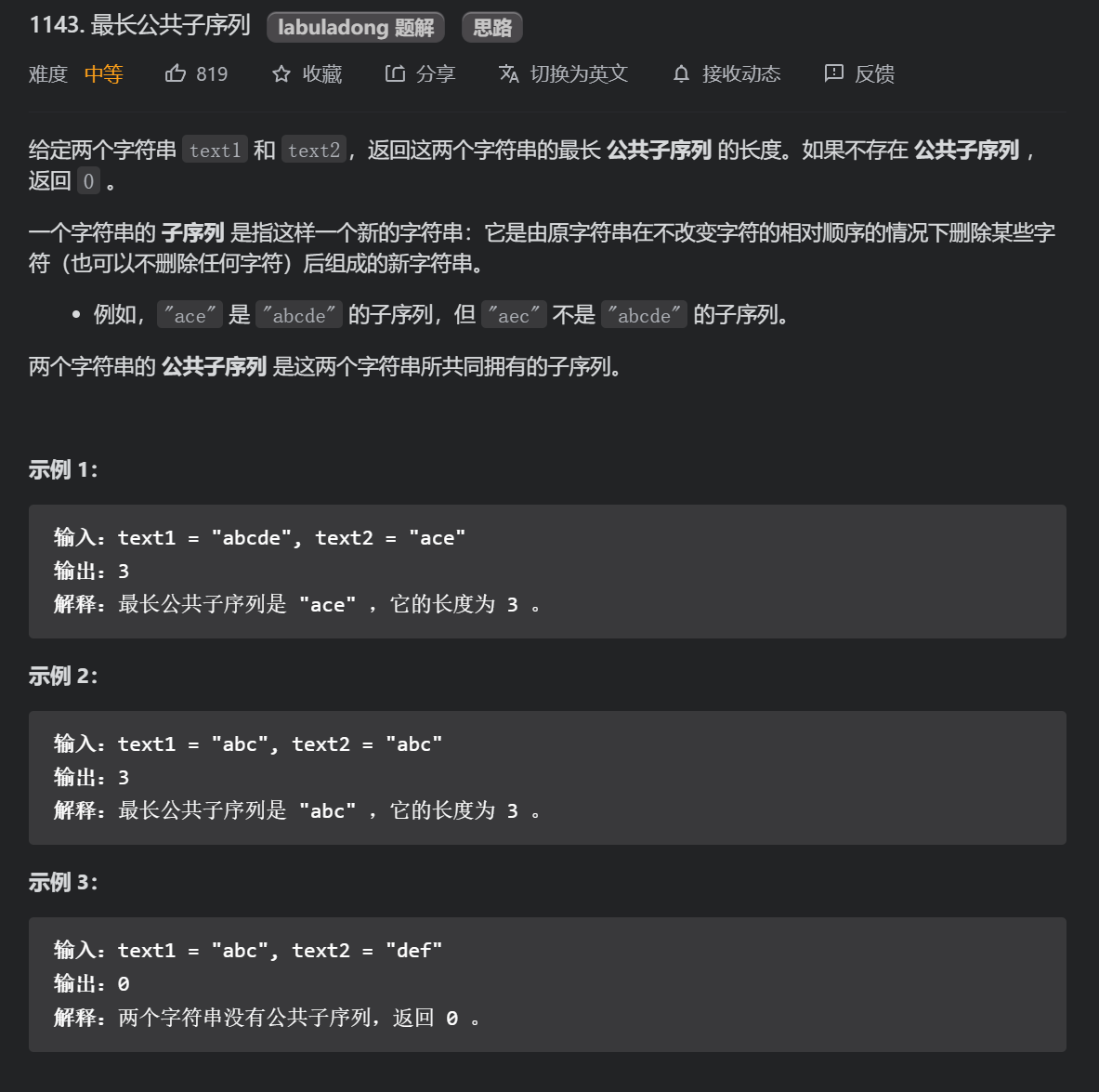
Pay attention to the requirements of the topic, and the longest public sequence can be deleted.
Use dp[i][j] to record the length of the longest common subsequence of text1[1... I] and text2[1... J], then for all I, dp[i][0] = 0, because text2 does not contain characters; For all j, dp[0][j] = 0.
For dp[i][j], text1 and text2 both add one character compared to dp[i - 1][j - 1], so if text1[i] == text2[j], then dp[i][j] should be = dp[i-1][j-1] + 1.
If text1 [i]= Text2 [J], how to deal with it?
Returning to the meaning of dp array, it refers to the length of the longest common subsequence between text1[1... I] and text2[1... j]. It only refers to the longest length, but it does not say that text1[i] and text2[j] must be included. The title also says that some characters in some strings can be deleted, but the order cannot be changed. Therefore, when the current characters are different, we should delete the current characters, But there are two ways to delete: delete text1[i] or text2[j], which one? We want to keep the maximum value, so dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
Why not consider dp[i-1][j-1] when waiting?
Because dp[i-1][j] already includes the case of dp[i-1][j-1], dp[i-1][j-1] is either equal to dp[i-1][j], or dp[i-1][j-1] + 1 = dp[i-1][j], so the case is included.
To sum up, the state transition equation is:
if text1[i] == text2[j]:
dp[i][j] = dp[i-1][j-1]
if text1[i] != text2[j]:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
In order to traverse all cases, we have to use a two-layer loop to ensure that all j or i are traversed when i or j is determined.
With the above thinking, you can write the corresponding code: (note that we assume that the subscript starts from 1, because it is convenient to discuss the case without characters)
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 0; i <= len1; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= len2; i++) {
dp[0][i] = 0;
}
// dp[i][j]: indicates the LCS length of text1[1...i] and text2[1...j]
// Note that text1[i] and text2[j] need not be included
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
※ 2.1.1 longest repeating subarray (medium)
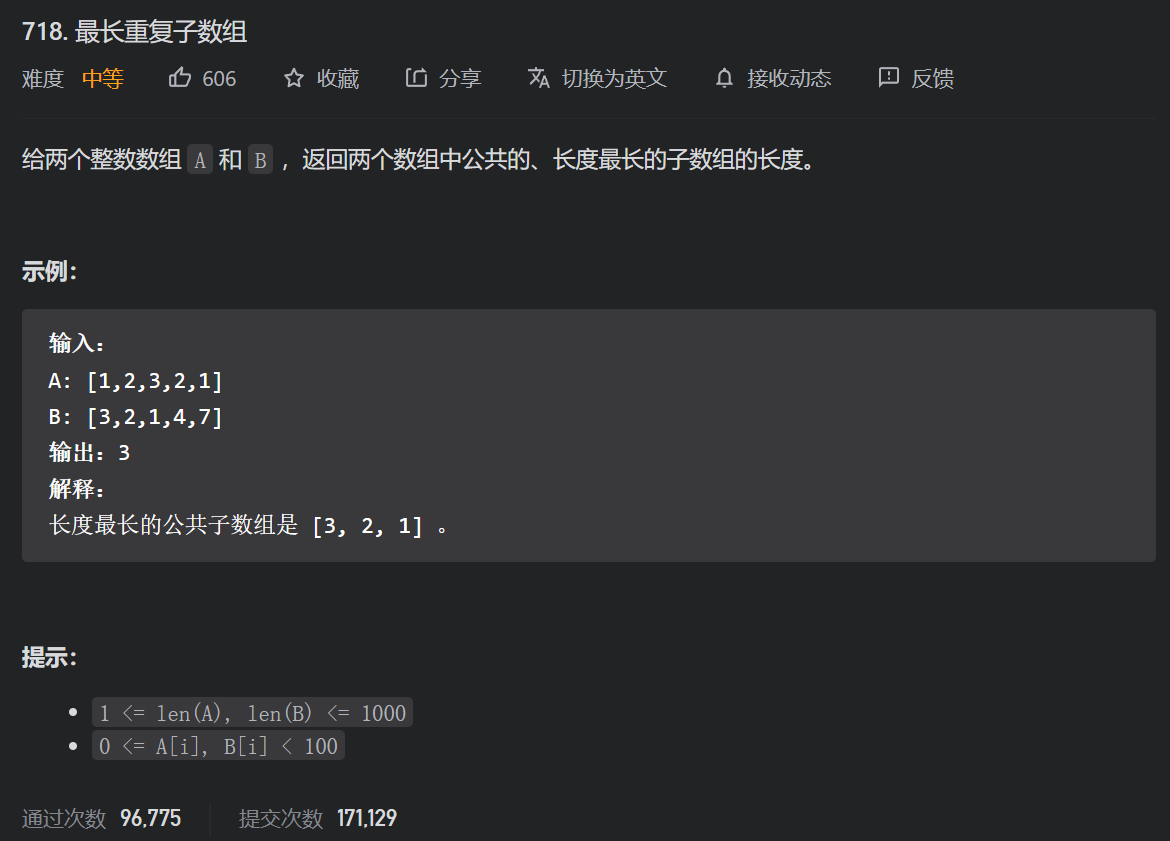
Note that the title requirements are public and cannot be deleted.
Is the meaning of dp[i][j] the same as before? (template of the previous question) represents the length of the longest repeating subarray of A[1... I] and B[1... j]?
When A[i] == B[j], dp[i][j] = dp[i - 1][j - 1] + 1
When a [i]= When B [J], dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
Right?
give an example
01111
10101
When I to the third number and j to the fifth number, A[i] == B[j], dp[i][j] = dp[i - 1][j - 1] + 1 = 2 + 1 = 3, it is obviously wrong and should be 2. Because the above transfer equation is for elements that can be deleted. If elements cannot be deleted, once the elements are unequal, it should be set to 0, that is, dp[i][j] = 0. Once it is set to zero, the meaning of dp array also changes. It should be the length of the longest repeating sub array ending in A[i] and B[j].
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] dp = new int [len1 + 1][len2 + 1];
// DP [i] [J]: longest common repeating subarray of nums1 [1... I] and nums2[1...j]
// Note: deletion is not allowed in the title
// nums1[i] == nums2[j]: dp[i][j] = dp[i - 1][j - 1] + 1
// nums1[i] != nums2[j]: dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
int max = 0;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = 0;
}
max = Math.max(max, dp[i][j]);
}
}
return max;
}
}
2.1.2 deletion of two characters (medium) (adaptation question 1)
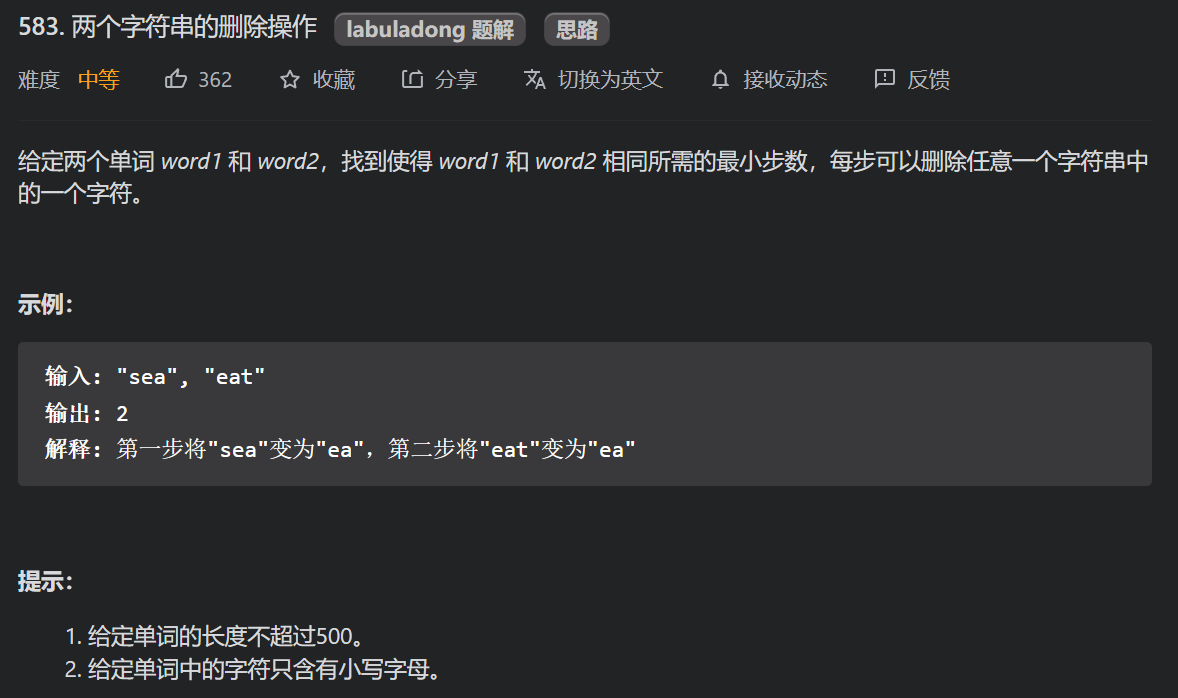
According to the meaning of the title, the two words must be the same. If they are different, delete the same word.
dp[i][j] represents the minimum number of steps between text1[1... I] and text2[1... j]. Let's look at the case where a string is all 0:
dp[i][0] = i, dp[0][j] = j, because one string is 0, the other string must be deleted to be the same
Let's look at the general situation. When text1[i] == text2[j]:
That is, the two strings do not need to be deleted. dp[i][j] = dp[i-1][j-1]
When text1 [i]= How to consider text2 [J]?
Either delete text1[i] or text2[j]. Considering the meaning of dp array, we must ensure that the problems considered later are independent and can be derived from the previous sub problems. Therefore, dp[i][j] = min(dp[i-1][j], dp[i][j-1])+1. dp[i-1][j-1] is not considered because this state has been included.
I really don't know whether it's right or not. I can give examples to verify it!
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
// dp[i][j] refers to the minimum number of steps of word1[1...i] and word2[1...j]
for (int i = 0; i <= len1; i++) {
dp[i][0] = i;
}
for (int i = 0; i <= len2; i++) {
dp[0][i] = i;
}
// Delete or not delete some characters so that word1 and word2 are the same
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
// Equality should not be deleted
dp[i][j] = dp[i - 1][j - 1];
} else {
// Unequal
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
}
return dp[len1][len2];
}
}
2.1.3 minimum ASCII deletion sum of two strings (medium) (adaptation question 2)
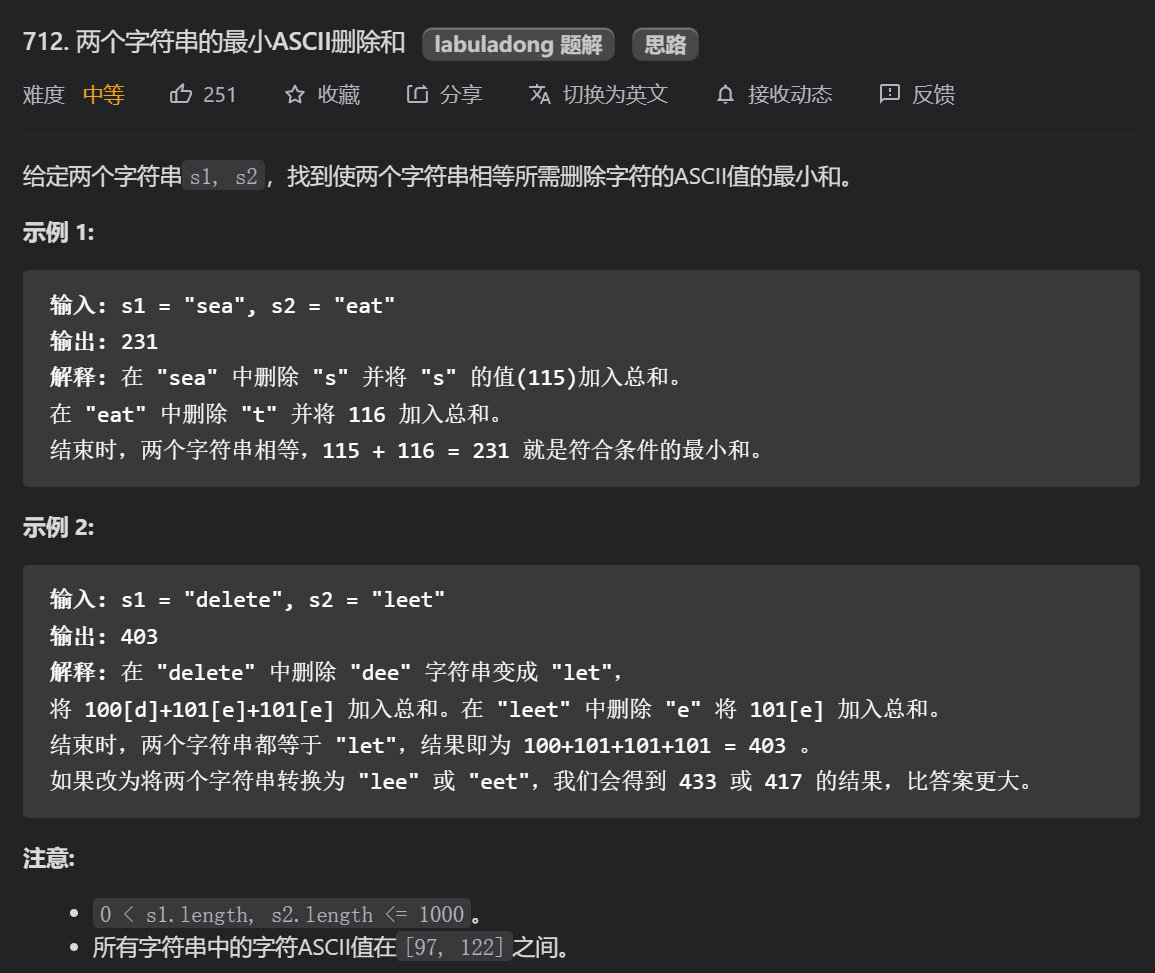
If you understand the first two questions, you can write this question directly. It's just that the meaning of dp array and base case have changed, and the state transition equation has been fine tuned.
The initialization of dp array becomes the addition of ASCII.
dp[i][j] refers to the minimum ASCII code deletion sum of text1[1... I] and text2[1... j]. Two cases are also discussed, text1[i] == text2[j]; text1[i] != text2[j], you can push it by hand (or push it back step by step from the simplest situation, or verify it with a simple situation after writing it).
class Solution {
public int minimumDeleteSum(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
// To make two strings equal, the ASCII value of the deleted character is the smallest
// dp[i][j] is the minimum sum of s1[1...i] and s2[1...j]
int sum = 0;
for (int i = 1; i <= len1; i++) {
sum += s1.charAt(i - 1);
dp[i][0] = sum;
}
sum = 0;
for (int i = 1; i <= len2; i++) {
sum += s2.charAt(i - 1);
dp[0][i] = sum;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
// The characters are equal and inherit directly from the front
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
// If the characters are different, compare the size of ASCII code to see which one to delete
dp[i][j] = Math.min(dp[i - 1][j] + s1.charAt(i - 1), dp[i][j - 1] + s2.charAt(j - 1));
}
}
}
return dp[len1][len2];
}
}
2.1.4 disjoint lines (medium)

Drawing, starting from the simplest case, dp[i][j] represents the most lines that nums1[1... I] and nums2[1... j] can draw.
When nums1[i] == nums2[j], you can draw a line. Once it is drawn, neither nums1[i] nor nums2[j] can be used as the end point of the line, because the subject has requirements. So dp[i][j] = dp[i - 1][j - 1] + 1. It's not easy to think of it directly. You can give a few examples.
When nums1[i]= nums2[j], that is, you can't draw a line, so nums1[i] or nums2[j] can be used as the endpoint of the line, so dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]).
In fact, if you taste carefully, this problem is the longest common subsequence. If you change the soup without changing the dressing, the state transition equation remains unchanged.
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
// DP [i] [J]: the maximum number of lines that nums1 [1... I] and nums2[1...j] can draw at most
int[][] dp = new int [len1 + 1][len2 + 1];
// nums1[i] == nums2[j] dp[i][j] = dp[i - 1][j - 1] + 1
// nums1[i] != nums2[j] dp[i][j] = max(dp[i-1][j], dp[i][j-1])
for (int i = 1; i <= len1; i++) {
for (int j = 1;j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
2.1.5 edit distance (difficult)
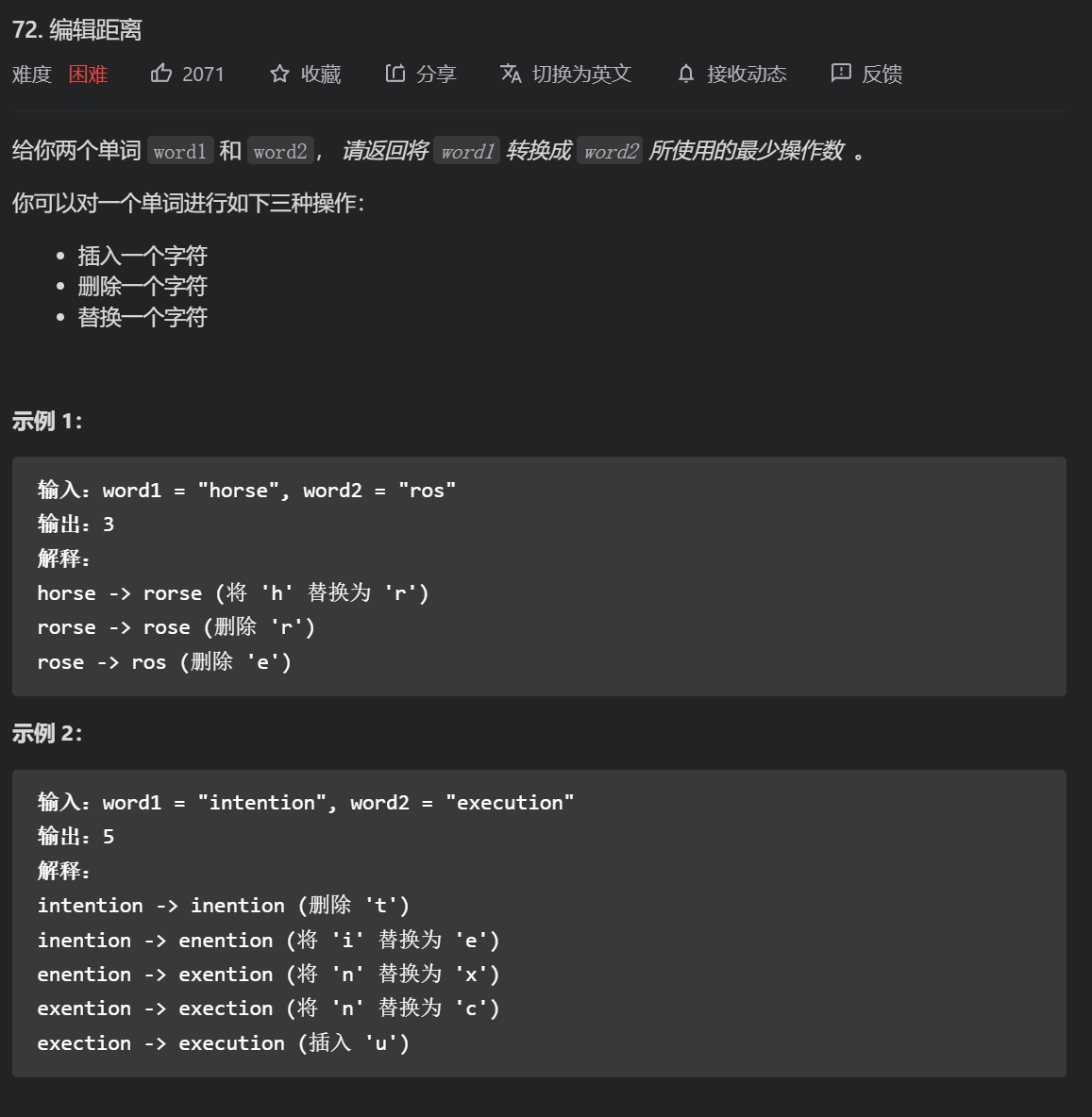
If this question has the foreshadowing of the above questions, it is easy to think of, mainly word1 [i]= Word2 [J] needs to be understood, because there are three cases in total, so let's discuss these three cases. We can draw a specific DP array, as shown in the following figure:
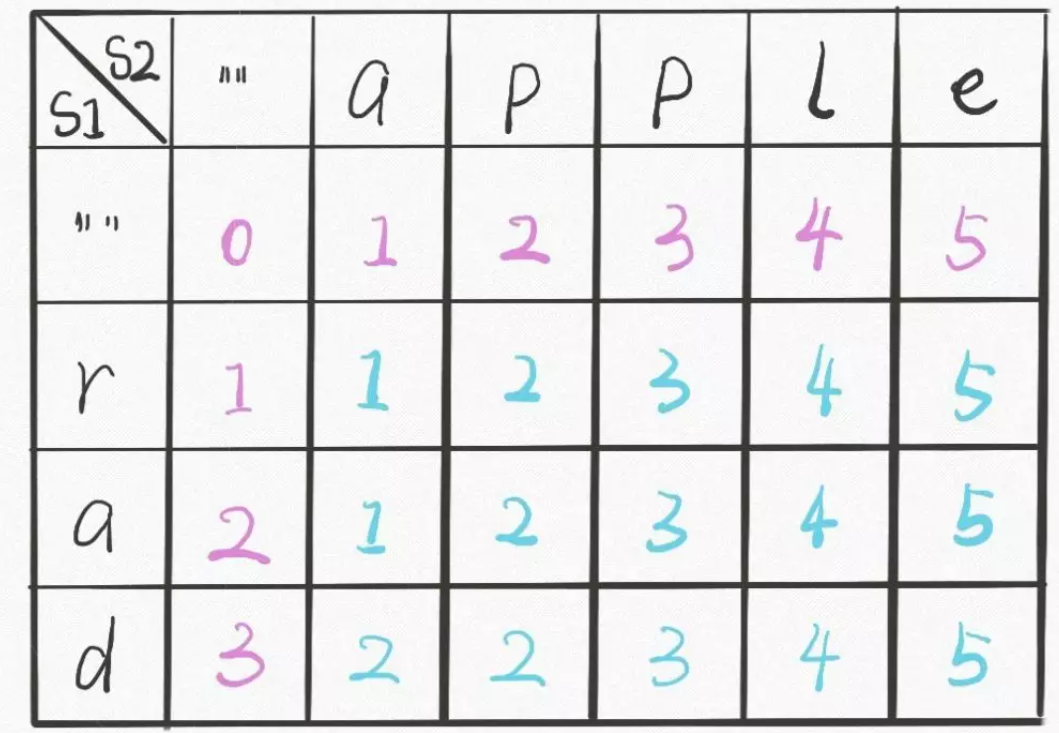
Source: labuladong official account edit distance topic
It can be seen from the above figure that each block can only be transferred from its upper left corner, upper part and left. You can try to deduce the state transition equation. In fact, it is easy to get the equation if you can draw the dp array directly when you encounter a strange dynamic programming problem.
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
// If the other string is empty, you can delete as many as you want
// It can also be inserted on the empty string all the time
dp[i][0] = i;
}
for (int j = 1; j <= len2; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
// Equal, no need to do anything
dp[i][j] = dp[i - 1][j - 1];
} else {
// Inequality is discussed in three cases,
dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
}
}
}
return dp[len1][len2];
}
}
2.1.6 judgment subsequence (simple) (double pointer, DP)
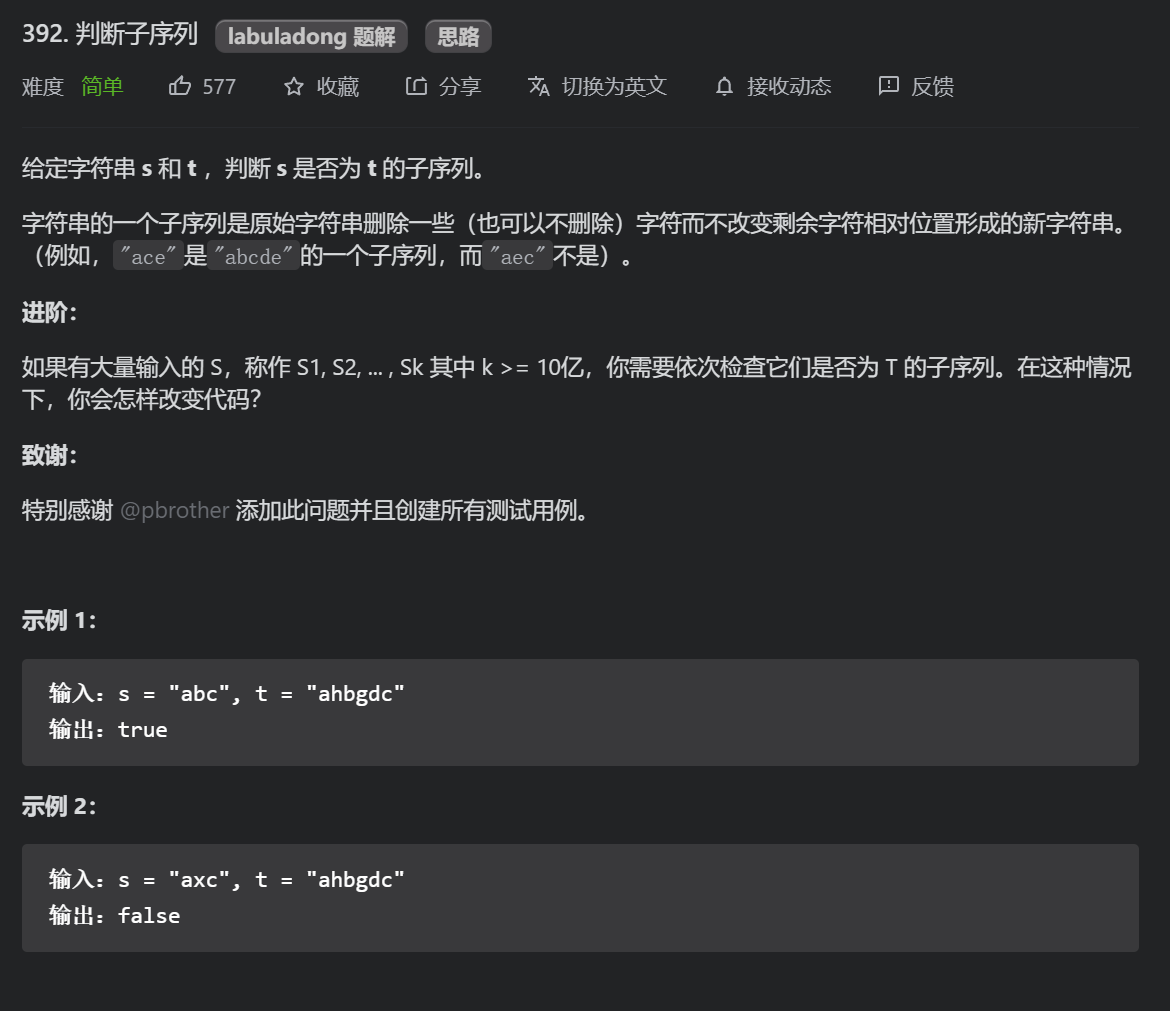
This problem is very simple if you use double pointers. If you use DP, you have to think of LCS.
Double pointer solution:
class Solution {
public boolean isSubsequence(String s, String t) {
int i = 0;
int j = 0;
if (s.length() == 0) {
return true;
}
while (j < t.length()) {
if (s.charAt(i) == t.charAt(j)) {
i++;
}
if (i == s.length()) {
break;
}
j++;
}
return i == s.length();
}
}
DP solution:
Very simple. According to the LCS solution and statistics dp[i][j], it should be noted that the s string cannot be deleted, only the t string can be deleted! See whether the length of the last dp[len1][len2] is equal to len1.
class Solution {
public boolean isSubsequence(String s, String t) {
int len1 = s.length();
int len2 = t.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
// You can only delete the t string in the title, not the s string!
dp[i][j] = dp[i][j - 1];
}
}
}
return dp[len1][len2] == len1;
}
}
※※ 2.1.7 different subsequences (difficult)
At first glance, this question has the shadow of the longest common subsequence, because each case can be regarded as whether a substring of s string = t, and then count the number of satisfied substrings.
dp[i][j] array represents the number of subsequences of s in t under the conditions of s[1... I] and t[1... j]. dp[i][0] = 1. It is true for I from 0 to len1, because the empty string is the substring of all strings. It should appear once when counting the number of empty strings.
When s[i] == t[j], take s = "rara" t = "ra" as an example. When I = 3 and j = 1, s[i] == t[j]. At this time, there are two cases. The s string uses the last bit of a and does not use the last bit of A.
- If the a of the last bit of s string is used, the a of the last bit of t string is also consumed. At this time, the subsequence is actually = dp[i-1][j-1]
- If you don't use the a of the last bit of s string, it depends on whether there is a "ra" subsequence in "rar", that is dp[i-1][j]
- Therefore, dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
When s [i]= When t [J], because t string cannot be deleted, only s string can be deleted, so dp[i][j] = dp[i - 1][j].
class Solution {
public int numDistinct(String s, String t) {
int len1 = s.length();
int len2 = t.length();
int[][] dp = new int[len1 + 1][len2 + 1];
// If t is an empty string, there is only one case
for (int i = 0; i <= len1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
// According to the meaning of the title, only the characters in the s string can be deleted, t cannot be deleted
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[len1][len2];
}
}
In fact, this problem is not easy to think of the transfer equation when the characters are the same, which can be obtained after trying.
2.2 problems involving only single string and array
2.2.1 palindrome substring (medium)
Note: substrings with different start or end positions, even if they are composed of the same characters, will be regarded as different substrings.
d p [ i ] [ j ] number group surface show s [ i . . . j ] yes no can structure become return writing strand The dp[i][j] array indicates whether s[i...j] can form a palindrome string The dp[i][j] array indicates whether s[i...j] can form a palindrome string
- From the above definition, dp[i][i] = true (1 < = I < = n, here we assume that s starts with subscript 1), because each character can form a palindrome
- Considering different characters, if s[i] == s[j] (we guarantee 1 < = I < = J < = n), then dp[i][j] = dp[i + 1][j - 1]. As can be seen from the following figure, if dp[i + 1][j - 1] is palindrome, when s[i] = s[j], dp[i][j] should also be palindrome. So, in fact, the state in this question extends from the middle to both sides.
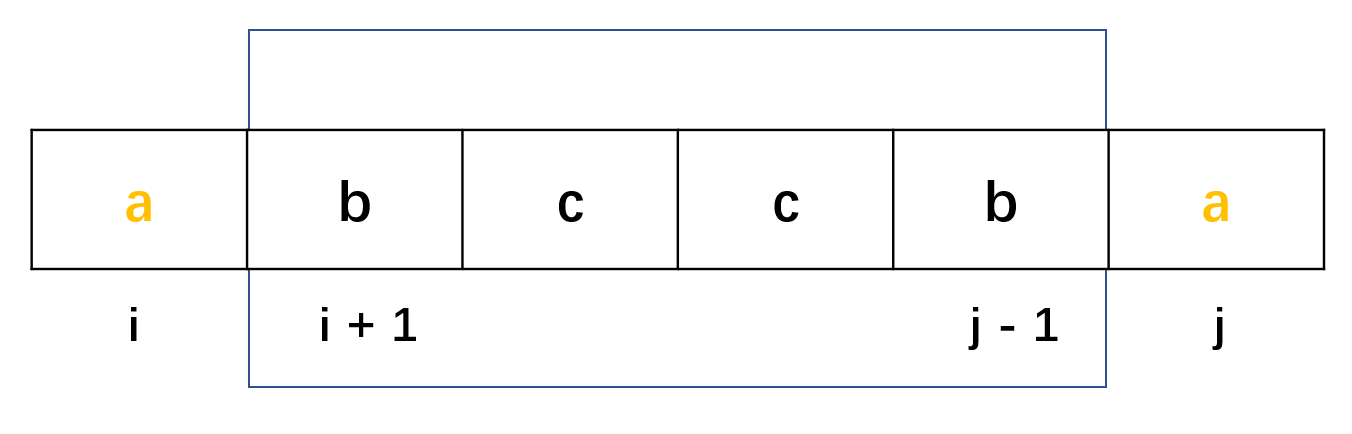
- If s[i]= S [j], then no matter whether it is a palindrome string or not, s[i... j] cannot be a palindrome string, so dp[i][j] = false.
- Considering the generality of the state transition equation, when there are only two characters, s[i] = s[j], dp[i][j] = dp[i + 1][j - 1], it will cause j to run in front of I, which is invalid. How should this state be converted? As in the case of only one character, we can judge it specially, because if two characters are equal, it must be palindrome. Similarly, when there are three characters, if the characters on both sides are equal, it must be palindrome, but the state of three characters can be converted from the state of one character, so there is no need for special judgment.
Now that we have judged all possible palindrome strings and returned to the topic, we need to count the number of palindrome strings. In fact, we can judge and sum them when the state changes.
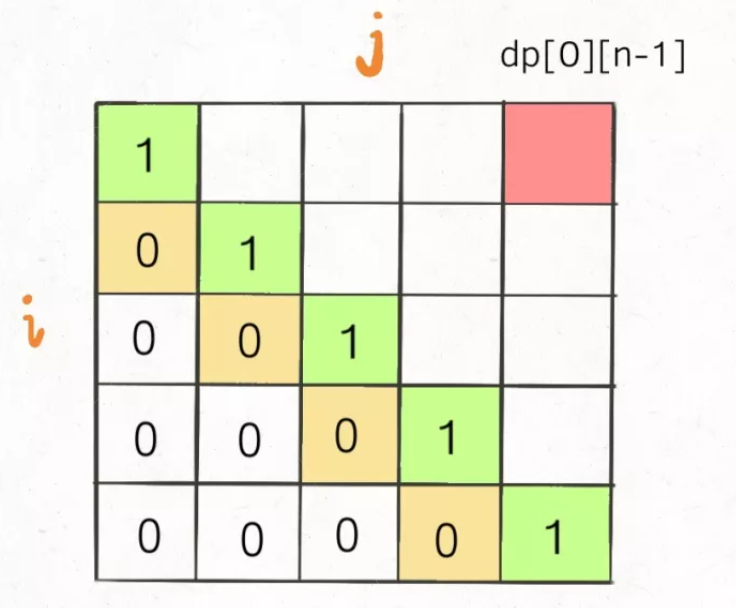
※: we also need to pay attention to the order of traversing the string, because dp[i][j] = dp[i + 1][j - 1], we must know I + 1 to deduce I. So I should be traversed from n.
3, How to determine the traversal order of the array?
1. In the process of traversal, the required state must have been calculated
2. The end point of traversal must be the location where the result is stored (the result of this question is dp[1][n])
class Solution {
public int countSubstrings(String s) {
// Can dp[i][j] s[i...j] form a palindrome string
int n = s.length();
boolean[][] dp = new boolean[n + 1][n + 1];
int cnt = 0;
for (int i = n; i >= 1; i--) {
// Note the order of traversal: 1. In the process of traversal, the required state must have been calculated
// 2. The end point of traversal must be the location where the result is stored (the result of this question is dp[1][n])
// j is smaller than i, which is meaningless. Ignore it
for (int j = i; j <= n; j++ ) {
if (s.charAt(i - 1) == s.charAt(j - 1)) {
if (j - i == 1 || j == i) {
// The special judgment length is 2
dp[i][j] = true;
cnt++;
} else {
dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j]) {
cnt++;
}
}
} else {
dp[i][j] = false;
}
}
}
return cnt;
}
}
2.2.2 longest palindrome substring (medium)
With the foreshadowing of the previous question, this question is very simple. Use dp array to record whether s[i... j] can form a palindrome string, and then judge the longest palindrome string when it can form a palindrome string.
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
if (n == 1) {
return s;
}
boolean[][] dp = new boolean[n + 1][n + 1];
// dp[i][j] = dp[i + 1][j - 1]
int max = 1;
// Think subscripts start with 1
int start = 1;
for (int i = n; i >= 1; i--) {
for (int j = i; j <= n; j++) {
if (s.charAt(i - 1) == s.charAt(j - 1)) {
if (j - i == 1 || j == i) {
// Special judgment of two characters and one character
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// Update longest palindrome string
if (dp[i][j] == true && max < (j - i + 1)) {
start = i;
max = j - i + 1;
}
}
}
// Pay attention to the use of substring!
return s.substring(start - 1, start - 1 + max);
}
}
2.2.3 longest palindrome subsequence (medium)
The overall idea is similar to the previous questions, but one more sentence can delete or not delete characters, which means in s [i]= S [J], the state transition equation will be different.
If s[i]= s[j], then we can delete s[i] or s[j] (the cases of simultaneous deletion have been included). The longest palindrome string can only be generated in those two cases. So, dp[i][j] = max (dp[i + 1][j], dp[i][j - 1])
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n + 1][n + 1];
// s[i] == s[j] : dp[i][j] = dp[i+1][j-1] + 2
// s[i] != s[j] : dp[i][j] = max(dp[i+1][j], dp[i][j-1])
for (int i = n; i >= 1; i--) {
for (int j = i; j <= n; j++) {
if (i == j) {
dp[i][j] = 1;
} else {
if (s.charAt(i - 1) == s.charAt(j - 1)) {
if (j - i == 1) {
// First judge the case of two characters, because it cannot be obtained through equation transfer
dp[i][j] = 2;
} else {
dp[i][j] = dp[i + 1][j - 1] + 2;
}
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
}
return dp[1][n];
}
}
2.2.4 maximum subarray sum (simple)
Consider that an element has two states: select it or not.
class Solution {
public int maxSubArray(int[] nums) {
int n = nums.length;
int[] dp = new int[n + 1];
// dp[i], the sum of the largest subarray ending with the ith number
// Note that the subarray contains at least one element
dp[1] = nums[0];
// For a number, we can choose or not
int max = dp[1];
for (int i = 2; i <= n; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i - 1], nums[i - 1]);
max = Math.max(dp[i], max);
}
return max;
}
}
2.2.5 longest continuous increasing sequence (simple)
Note that deletion is not allowed. It must be continuous and strictly increasing. It is also to write the transfer equation according to the two states of the element, dp[i] refers to the length of the longest continuous increasing sequence ending with the ith element.
class Solution {
public int findLengthOfLCIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n + 1];
// The longest continuous increasing sequence ending with the ith number (cannot be deleted)
dp[1] = 1;
int max = 1;
for (int i = 2; i <= n; i++) {
if (nums[i - 1] > nums[i - 2]) {
dp[i] = dp[i - 1] + 1;
} else {
dp[i] = 1;
}
max = Math.max(max, dp[i]);
}
return max;
}
}
2.2.6 longest increasing subsequence (medium)
Pay attention to the meaning of the title. It is strictly incremented. The position of array elements cannot be changed, but they can be deleted!, Considering an element num [i] in the array, dp[i] represents the length of the longest strictly increasing subsequence ending with the i-th element, so dp[i] = max(dp[j]) + 1, j refers to the number before the I subscript and strictly less than num [i], so it is necessary to traverse all cases, because the elements in the middle may be deleted, for example: 2 1 3, the result should be 2, because 1 can be deleted.
After the above analysis, in fact, this problem also needs to traverse all situations, but the judgment conditions are different.
class Solution {
public int lengthOfLIS(int[] nums) {
// The longest strictly increasing subsequence can be deleted, but the element order cannot be changed
// dp[i], the length of the longest increasing subsequence ending with the ith number
int n = nums.length;
int[] dp = new int[n];
// The 0 th number, there is only one number, and the length is 1
dp[0] = 1;
// dp[i] = max(dp[j]) + 1, max(dp[i]) refers to the longest length that can form a strictly increasing subsequence
int max_len = 1;
// Traverse all possible situations
for (int i = 1; i < n; i++) {
// The default is only yourself, with a length of 1
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
max_len = Math.max(max_len, dp[i]);
}
return max_len;
}
}
Singular group, string template
Except for palindrome substring questions, they are generally solved with one-dimensional DP array, dp[i], representing xxx ending with the ith element.
Palindrome string is a two-dimensional DP array, dp[i][j], indicating whether the substring [I... j] is a palindrome condition.
Two array and string templates
Generally, a two-dimensional DP array, dp[i][j], is used to represent the xxxx conditions of t[1... I] and s[1... J]. Pay attention to the meaning of DP array of the longest repeating sub array, and add a condition ending with the ith number and the j number.
At the same time, in either case, we must pay attention to the direction of traversal.