BFS question: PIPI's safe

Question:

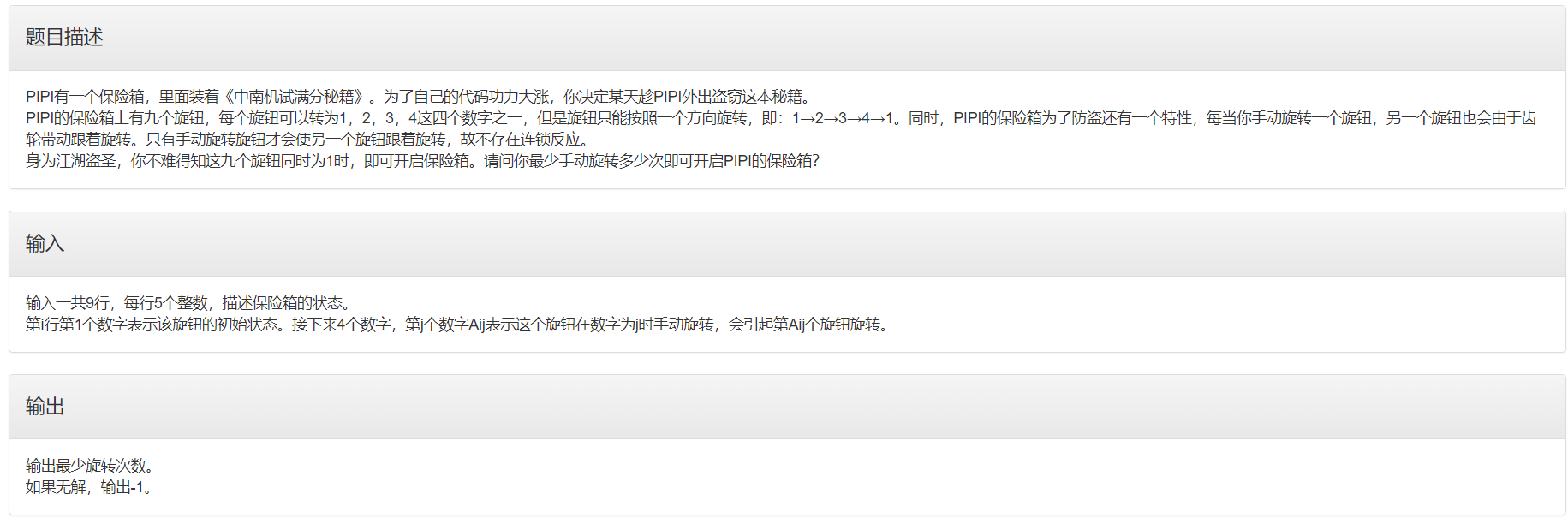
Idea:

  we need to find the minimum operand from the initial state to the final state, which can be solved by BFS. For each operation, we can rotate any of the 9 knobs, that is, a state can derive 9 sub states.
  how to store the status of 9 knobs? We can use a one-dimensional array to represent the states of 9 knobs, the subscript corresponds to the knob, and the value corresponds to the number indicated by the knob. The one-dimensional array is stored in the queue together with the operands spent to reach the state.
    for the number indicated by the knob, we can reduce it by 1, that is, 0,1,2,3 represents 1,2,3,4 in the question; In this way, we can get the number indicated after rotation by adding 1 and taking the modulus of 4.
   how to represent the tag array, that is, how to indicate whether the current state has been accessed? Maybe it can be represented by a 9-dimensional array, viz [4] [4] [4] [4] [4] [4] [4] [4]. If the number indicated by the 9 knobs is 123412341, then vis [0] [1] [2] [3] [0] [1] [2] [3] [0] = 1; However, we have a better way. We can use a quaternary number to represent the state. For example, state 333333330 can be regarded as a quaternary number: 3 * 4 ^ 8 + 3 * 4 ^ 7 + 3 * 4 ^ 6 +... + 0 * 4 ^ 0.
   use a two-dimensional array relation[9] [4] to represent linkage, and relation[i] [j] to represent knob I. when indicating j, operating it will rotate knob relation[i] [j]

Points to note:

• In bfs, you need to pop up the first element of the queue, and then change the value of its state array. Set the array as int[] new. When traversing 9 subsequent States, you need to re create an array and assign the value of each element of int[] new to it. Instead, you can't use int[] temp = new. In this way, temp will become a reference to new. Modify temp and new that you didn't want to modify
• Note that the initial state is the open state of the safe, and 0 is directly output at this time

code:

import java.util.*;

public class Main {
    static int[] quantity = new int[9];
    static Set<Long> set = new HashSet<>();
    static LinkedList<Node> q = new LinkedList<>();
    static int[][] relation = new int[9][4];
    public static void main(String[] args) {
        int i, j;
        quantity[0] = 1;
        for (i = 1;i < 9;i++) {
            quantity[i] = quantity[i - 1] * 4;
        }
        Scanner scanner = new Scanner(System.in);
        int[] start = new int[9];
        for (i = 0;i < 9;i++) {
            for (j = 0;j < 5;j++) {
                if (j == 0) {
                    start[i] = scanner.nextInt() - 1;
                } else {
                    relation[i][j - 1] = scanner.nextInt() - 1;
                }
            }
        }
        q.add(new Node(start, 0));
        if (cal(start) == 0) {
            System.out.println(0);
            return;
        }
        if (!bfs()) {
            System.out.println(-1);
        }
    }

    static boolean bfs() {
        int i;
        long count;
        while (!q.isEmpty()) {
            Node now = q.pop();
            for (i = 0;i < 9;i++) {
                int[] temp = new int[9];
                for (int j = 0;j < 9;j++) {
                    temp[j] = now.status[j];
                }
                temp[relation[i][temp[i]]] = (temp[relation[i][temp[i]]] + 1) % 4;
                temp[i] = (temp[i] + 1) % 4;
                count = cal(temp);
                if (!set.contains(count)) {
                    if (count == 0) {
                        System.out.println(now.level + 1);
                        return true;
                    }
                    set.add(count);
                    q.add(new Node(temp, now.level + 1));
                }
            }
        }
        return false;
    }

    static long cal(int[] status) {
        long temp = 0;
        for (int i = 0;i < 9;i++) {
            temp += status[i] * quantity[i];
        }
        return temp;
    }

}

class Node {
    public int[] status;
    public long level;
    public Node(int[] status, long level) {
        this.status = status;
        this.level = level;
    }
}