Breadth first search
definition
Breadth first search, also known as breadth first search, is accessed layer by layer, which is similar to the hierarchical traversal of the tree. The vertices of the graph are many to many, and are accessed from near to far relative to the starting point until all nodes are accessed.
BFS traversal process
Starting from a vertex, access the adjacent points that are not accessed in turn. Access the adjacency points of these adjacency points in turn in the order of "the adjacency points of the first accessed vertices are accessed first", until the adjacency points of all the accessed vertices in the graph are accessed. If there are still vertices in the graph that have not been accessed at this time, select another vertex v that has not been accessed as the starting point, and repeat the above process until all vertices in the graph have been accessed
Algorithm implementation
Algorithmic thought
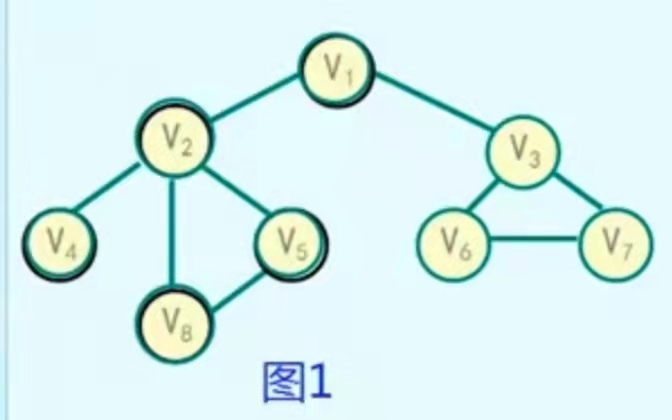
Breadth first search traversal reflects the characteristics of first in first out and queue.
After accessing v, visit the adjacent nodes V1 and V2 of v all the way to Vk. Finally, visit their adjacent points in the order of V1,V2 and Vk. V1 is accessed first before V1, and the adjacent points of V1 will also be accessed first before V2 and Vk. Therefore, it has the feature of first in first out, because the accessed vertices can be saved in a queue.
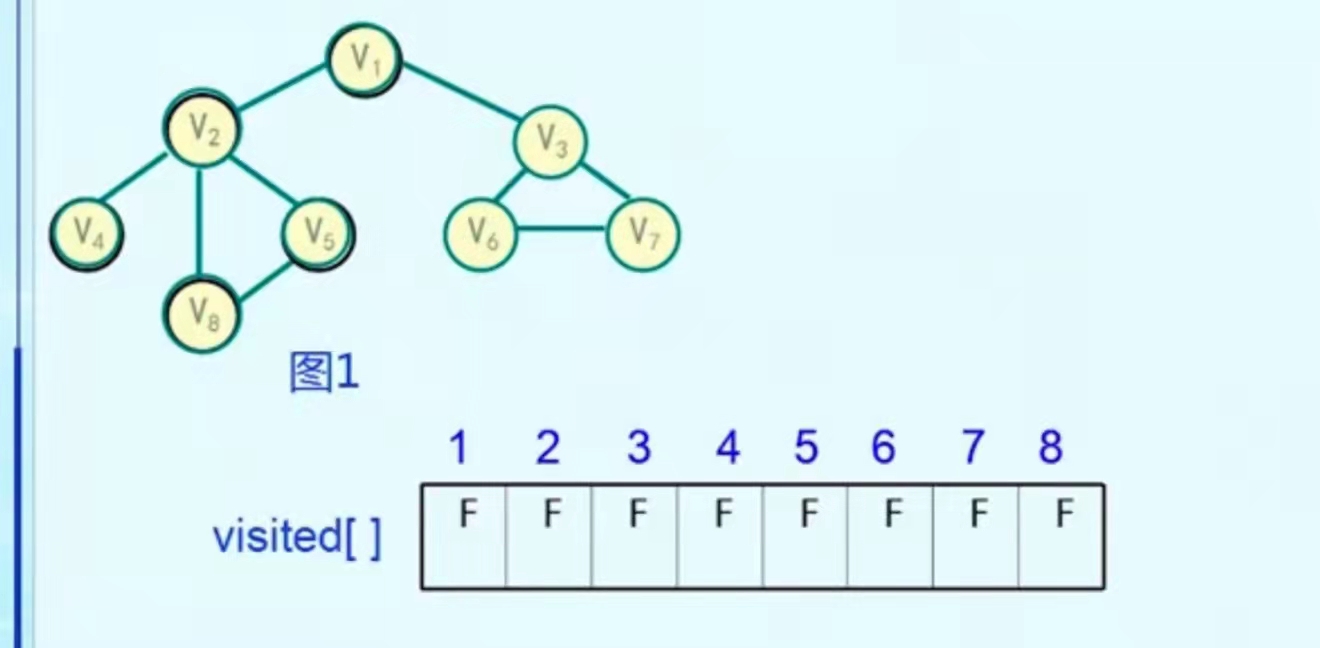
Set an access flag array. Before accessing, set the flag bit of each vertex to false. If a vertex is accessed, set the corresponding position of the array to true. Now place a queue. Whenever a vertex is accessed, it will be queued, and when its adjacent points are accessed, it will be dequeued.
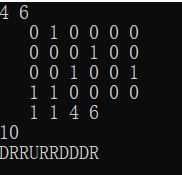
The final traversal results are V1, V2, V3, V4, V5, V8, V5, V6 and v7
The result of traversal is not unique, and the location of the same adjacent point of a node is not unique.
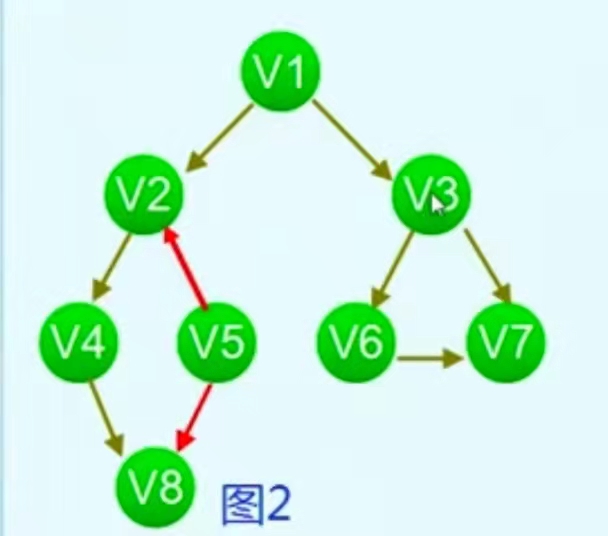
In the traversal of a directed graph, due to its unidirectionality, the graph will not be a strongly connected graph or a connected graph, that is, there are two or more connected subgraphs or strongly connected subgraphs. As shown in Fig. 2, there are two connected components. Finally, start from the second connected component V5 and perform breadth first traversal again.
Breadth first search algorithm of graph adjacency matrix
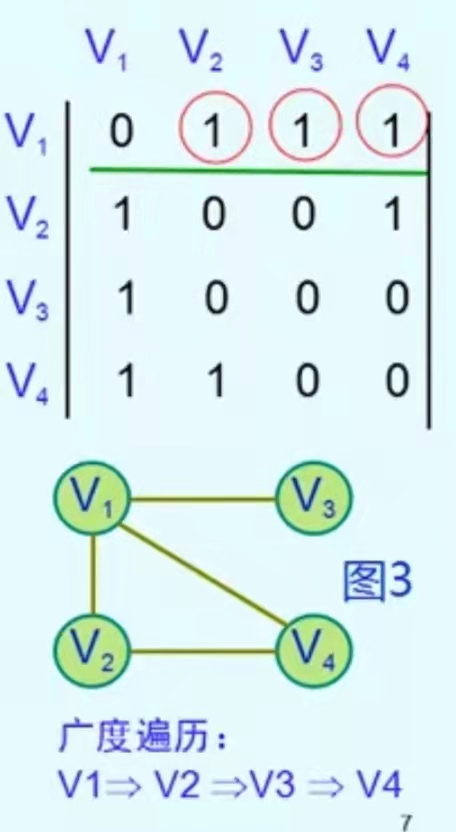
void BFSM(MGgrph *g,int k)//adjacency matrix
//Starting from V0, breadth first traversal graph G
{
int i,j;
initqueue(Q);//Initialize and set empty queue Q
enqueue(&Q,k);//To access my node, enter the queue Q
printf("%s",G->vex[k].info);
visited[k]=TURE;
while(!=QueueEmpty(&Q))//When the queue is not empty
{
i=dequeue(&Q);//Queue header element v out of queue
for(j=1;j<=G-n;;j++)
{
if(G->edges[i][j]==1&&visited[j]==0)
{
printf("%c",G->vex[j].info);
visited[j]=TURE;
enqueue(&Q,j);//Vj queue for visit
}
}
}
}//
Solving maze problem
case analysis
0 1 0 0 0 0
0 0 0 1 0 0
0 0 1 0 0 1
1 1 0 0 0 0
For such a simple maze, 1 in the figure indicates that the obstacles are impassable. It is required to find the path from the starting point in the upper left corner to the end point in the lower right corner, and find a path with the shortest required number of steps. If there are multiple optimal routes, sort them according to the dictionary order d < l < R < U.
For simplicity, define a point class to store the data of each vertex.
Set the variables along the X and Y directions respectively during the movement, and define a dir [] array to store the change of direction during the movement, which is consistent with the change of coordinates x and y.
struct point
{
int x;
int y;
int step;
string str;
};
queue<point> r;
int dx[4] = { 1,0,0,-1 };
int dy[4] = { 0,-1,1,0 };
char dir[4] = { 'D','L','R','U' };
Assign the coordinate information of the starting point, the access array flag is 1, the starting point has been accessed, and join the team.
point start; start.x = startx; start.y = starty; start.step = 0; v[startx][starty] = 1; int flag = 0; r.push(start);
//Access its adjacent vertices for each accessed node in turn
for (int k = 0; k <= 3; k++)
{
int tx, ty;
string str1;
tx = x + dx[k];
ty = y + dy[k];
str1 = str + dir[k];
if (v[tx][ty] == 0 && a[tx][ty] == 0)
{//The vertex is not an obstacle and is not accessed
point temp;//Define a temporary queue to merge with the previous queue
temp.x = tx;
temp.y = ty;
temp.step = r.front().step + 1;
temp.str = r.front().str +dir[k];
r.push(temp);
v[tx][ty] = 1;
}
When the leading edge nodes of the starting node are accessed, the starting node leaves the queue. When the queue is not empty, each cycle only needs to judge whether the value of the first vertex of the current queue is the same as the value of the input end coordinate.
if (x == p && y == q)
{
flag = 1;//There is an optimal path
cout << r.front().step << endl;
cout << r.front().str << endl;
break;
}
If there is no path from start to end, an error message is output.
if (flag == 0) cout << "no answer!" << endl;
code implementation
Complete code
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int a[100][100], v[100][100];
struct point
{
int x;
int y;
int step;
string str;
};
queue<point> r;
int dx[4] = { 1,0,0,-1 };
int dy[4] = { 0,-1,1,0 };
char dir[4] = { 'D','L','R','U' };
int main()
{
int m, n;
cin >> m >> n;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
//scanf("%d" ,&a[i][j]);
cin >> a[i][j];
int startx, starty, p, q;
cin >> startx >> starty >> p >> q;
point start;
start.x = startx;
start.y = starty;
start.step = 0;
v[startx][starty] = 1;
int flag = 0;
r.push(start);
while (!r.empty())
{
int x = r.front().x;
int y = r.front().y;
string str = r.front().str;
if (x == p && y == q)
{
flag = 1;
cout << r.front().step << endl;
cout << r.front().str << endl;
break;
}
for (int k = 0; k <= 3; k++)
{
int tx, ty;
string str1;
tx = x + dx[k];
ty = y + dy[k];
str1 = str + dir[k];
if (v[tx][ty] == 0 && a[tx][ty] == 0)
{
point temp;
temp.x = tx;
temp.y = ty;
temp.step = r.front().step + 1;
temp.str = r.front().str +dir[k];
r.push(temp);
v[tx][ty] = 1;
}
}
r.pop();
}
if (flag == 0)
cout << "no answer!" << endl;
}
Run test