1, ConnectedComponents algorithm

ConnectedComponents, that is, the connectome algorithm labels each connectome in the graph with id, and takes the id of the vertex with the smallest serial number in the connectome as the id of the connectome.

When the diagram is as follows:

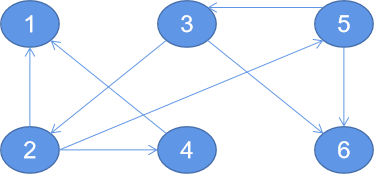
    //Create point
    val vertexRDD: RDD[(VertexId, (String,Int))] = SC.makeRDD(Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 50))
    ))

    //Creates an edge whose attributes represent the distance between two adjacent vertices
    val edgeRDD: RDD[Edge[Int]] = SC.makeRDD(Array(
      Edge(2L, 1L, 7),
      Edge(2L, 4L, 2),
      Edge(3L, 2L, 4),
      Edge(3L, 6L, 3),
      Edge(4L, 1L, 1),
      Edge(2L, 5L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3)
    ))

    //Point RDD + edge RDD = graph
    val graphDistance: Graph[(String, PartitionID), PartitionID] = Graph(vertexRDD, edgeRDD)
    
    ConnectedComponents
      .run(graphDistance,Int.MaxValue)
        .vertices.foreach(println)

The results are as follows

(5,1)
(3,1)
(6,1)
(2,1)
(4,1)
(1,1)

Process finished with exit code 0

When the diagram is as follows:

 

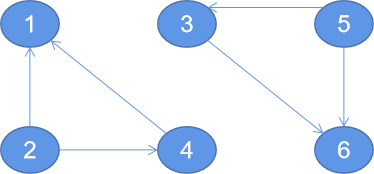
ConnectedComponents
    .run(graphDistance,Int.MaxValue)
    .vertices.foreach(println)

The results are as follows

(4,1)
(3,3)
(1,1)
(6,3)
(5,3)
(2,1)

Process finished with exit code 0

2, Stringlyconnected components algorithm

The largest strongly connected subgraph in a directed graph outputs the minimum vertex number corresponding to the vertex of each strongly connected subgraph.

The diagram is as follows:

StronglyConnectedComponents
    .run(graphDistance,Int.MaxValue)
    .vertices.foreach(println)

The results are as follows:

(6,6)
(4,4)
(3,2)
(5,2)
(1,1)
(2,2)

Process finished with exit code 0

Resolution: 1, 4 and 6 vertices cannot form a ring, so the minimum vertex id under stronglyconnected component is itself

2 - > 5 - > 3 form a strongly connected graph, so its minimum vertex id is 2

Application scenario ★★★

Talk list analysis character relationship
Enterprise information genealogy

3, ShortestPaths method

ShortestPaths is the shortest path from node to node that can be calculated. The minimum path is the minimum step size, not the shortest distance.

The diagram is as follows:

ShortestPaths
    .run(graphDistance,vertexRDD.map(_._1).collect().toSeq)
    .vertices.foreach(println)

The results are as follows:

(4,Map(4 -> 0, 1 -> 1))
(3,Map(2 -> 1, 5 -> 2, 4 -> 2, 1 -> 2, 3 -> 0, 6 -> 1))
(2,Map(2 -> 0, 5 -> 1, 4 -> 1, 1 -> 1, 3 -> 2, 6 -> 2))
(6,Map(6 -> 0))
(1,Map(1 -> 0))
(5,Map(2 -> 2, 5 -> 0, 4 -> 3, 1 -> 3, 3 -> 1, 6 -> 1))

Process finished with exit code 0

Application scenario ★★★

Internet of things (logistics)
Social interaction: six dimensional space (at most 5 people are separated between two people, i.e. the shortest path between two people < = 6)

4, LabelPropagation algorithm (did not understand the process)

LabelPropagation is a graph based semi supervised learning algorithm. Its application scenario is community detection. Community in the traditional sense refers to a group of nodes in the network with great similarity, resulting in a closely connected internal and sparse external group structure. According to the intersection of community nodes, it can be divided into non overlapping community and overlapping community. The process of finding the community structure of a given network graph is called "community discovery". Generally speaking, the process of community discovery is a clustering process.

Basic idea:

The application scenario of label propagation algorithm is non overlapping community discovery. Its basic idea is to take the largest number of labels in the labels of neighbor nodes of a node as the label of the node itself. A label is added to each node to represent the community to which it belongs, and the "community" structure of the same label is formed through the "propagation" of the label. In short, you belong to which label your neighbor belongs most. The advantage of the algorithm is that the convergence cycle is short, and there is no need for any a priori parameters except the number of iterations (the number and size of communities do not need to be specified in advance), There is no need to calculate any community index during the implementation of the algorithm.

Time complexity: the complexity of assigning labels to vertices is O(n), the time of each iteration is O (m), and the complexity of finding all communities is O (n +m). This is the time complexity of one iteration, not multiple iterations. The computational complexity of the label propagation algorithm is very cheap, but it does not guarantee convergence, and after enough iterations, all Unicom nodes finally converge to a community.

Communication process:

1) Initially, each node is given a unique label;

2) Each node updates its own label with the most of the labels of its neighbor nodes.

3) Repeat step 2) until the label of each node is no longer changed.

The update of a node label in an iteration can be divided into synchronous and asynchronous. The so-called synchronous update, that is, the label of node z in iteration t is based on the label obtained by its neighbor node in iteration t-1; Asynchronous update, that is, the label of node z in iteration t is based on the label of the node that has updated the label in iteration T and the label of the node that has not updated the label in iteration t-1. In short, synchronization means that all neighbor nodes have not been updated in this round. Node T is the first Updater. Asynchronous means that t is not the first Updater. There are both updated and not updated in this round in the neighbors.

matters needing attention:

1. A threshold value is set for the number of iterations to prevent over operation;

2. For bipartite graph and other network structures, synchronous update will cause oscillation;

3. A structure similar to (strong community >) (the community > =);

4. Each vertex is given a unique label at the beginning, that is, the "importance" is the same, and the iterative process adopts random sequence, which will lead to different results in the same initial state and even the emergence of giant communities;

5. If the "community center" point can be predicted, the accuracy of community discovery can be effectively improved and the efficiency can be greatly improved;

6. The label of neighbor nodes of the same node may have the same maximum number of multiple communities. Take "random" as its label

The diagram is as follows:

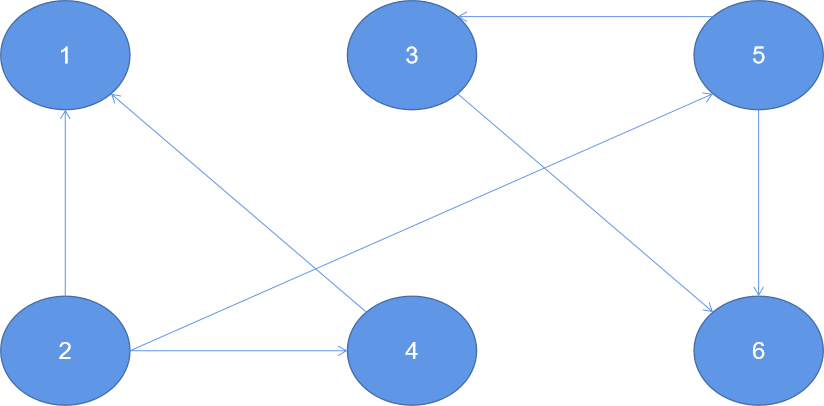
LabelPropagation
    .run(graphDistance,6)//The maximum number of iterations is generally set to the number of points
    .vertices.foreach(println)

The results are as follows:

(5,2)
(6,2)
(4,2)
(1,2)
(3,2)
(2,2)

Process finished with exit code 0

Resolution:

After the first iteration

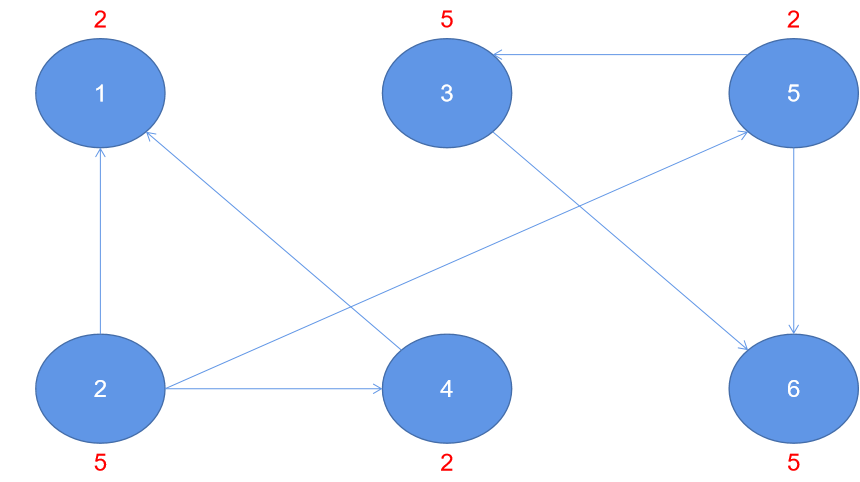
Second iteration

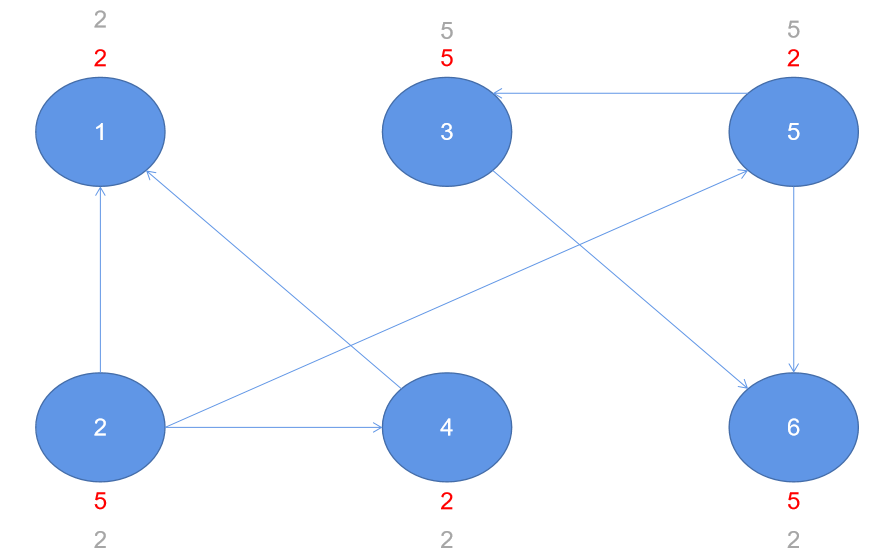
Third iteration

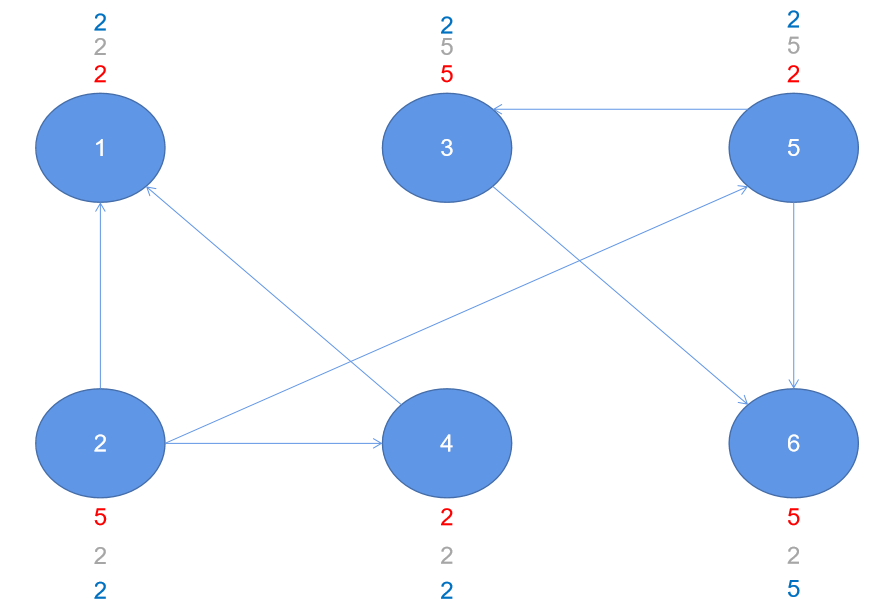
Fourth iteration

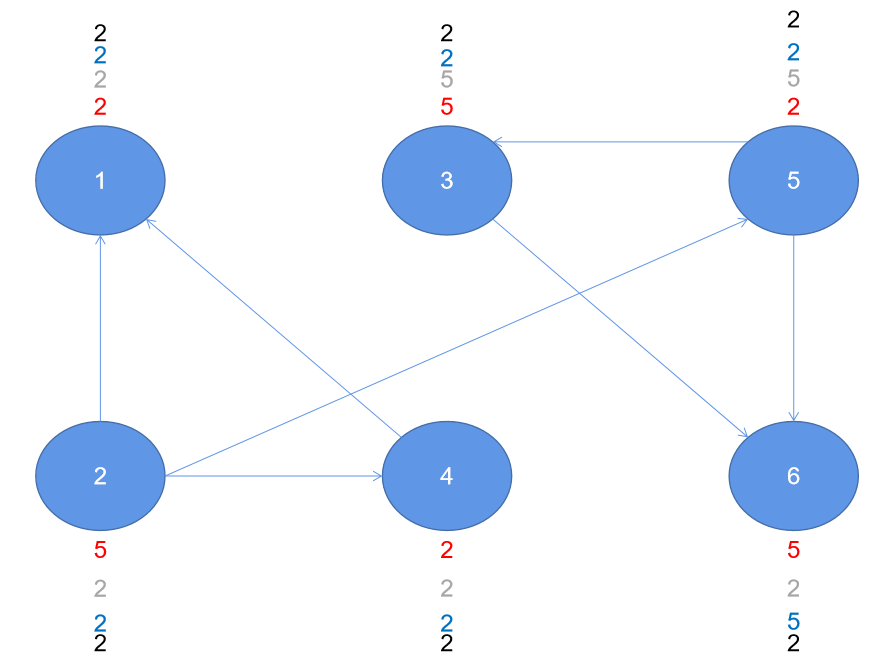
Application scenario ★★★

The game finds agents among players through chat records
Inference of information dissemination source: take the message as the theme and check the initiator of message dissemination

5, TriangleCount algorithm

The algorithm idea of Triangle Count is as follows:

1. Calculate the adjacent nodes of each node,
2. Calculate the intersection of the adjacent point set of the vertices connected by the two vertices of each edge, and find the node whose intersection id is greater than the first two node IDs,
3. Count the total number of triangles for each node. Note that only the triangles that meet the calculation direction are counted.

Note: when calculating triangles, there should be a calculation direction (for example, starting node id < intermediate node id < destination node id).

The diagram is as follows:

TriangleCount
    .run(graphDistance)
    .vertices.foreach(println)

The results are as follows:

(6,1)
(3,2)
(1,1)
(5,2)
(2,2)
(4,1)

Process finished with exit code 0

Application scenario ★★★

Community discovery: the closeness of community coupling (the more triangles in a person's social network, the more stable the social relationship is