Concept and operation of binary search tree
The concept of binary search tree
Binary search tree is also called binary sort tree. If its left subtree is not empty, the value of all nodes on the left subtree is less than that of the root node; If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of the root node, and its left and right subtrees are not binary search trees respectively. It can also be an empty tree.
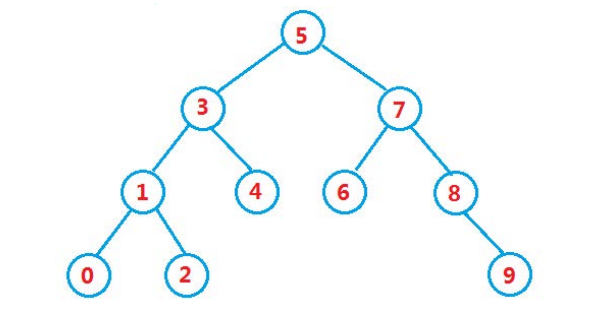
int a[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
Operation of binary search tree
lookup
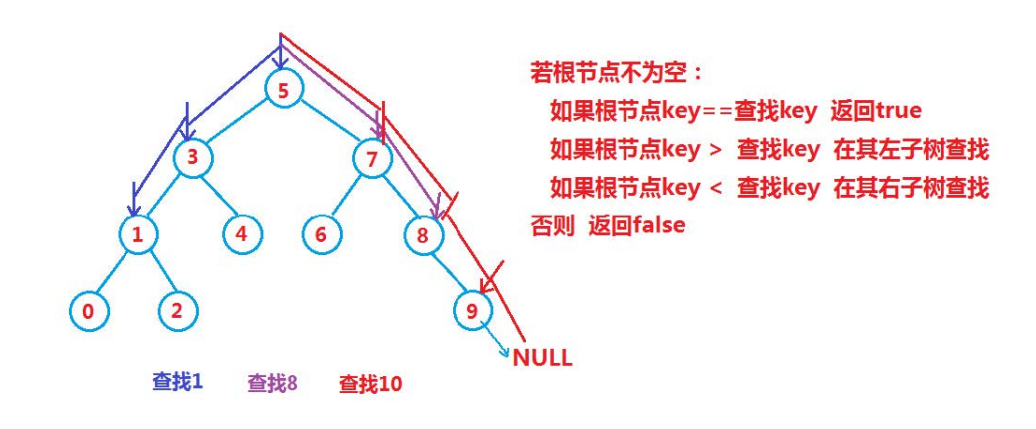
Iteration:
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
Recursion:
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
return nullptr;
if (root->_key < key)
return _FindR(root->_right, key);
else if (root->_key > key)
return _FindR(root->_left, key);
else
return root;
}
insert
- If the tree is empty, insert it directly

- The tree is not empty. Find the insertion position according to the nature of binary search tree and insert a new node
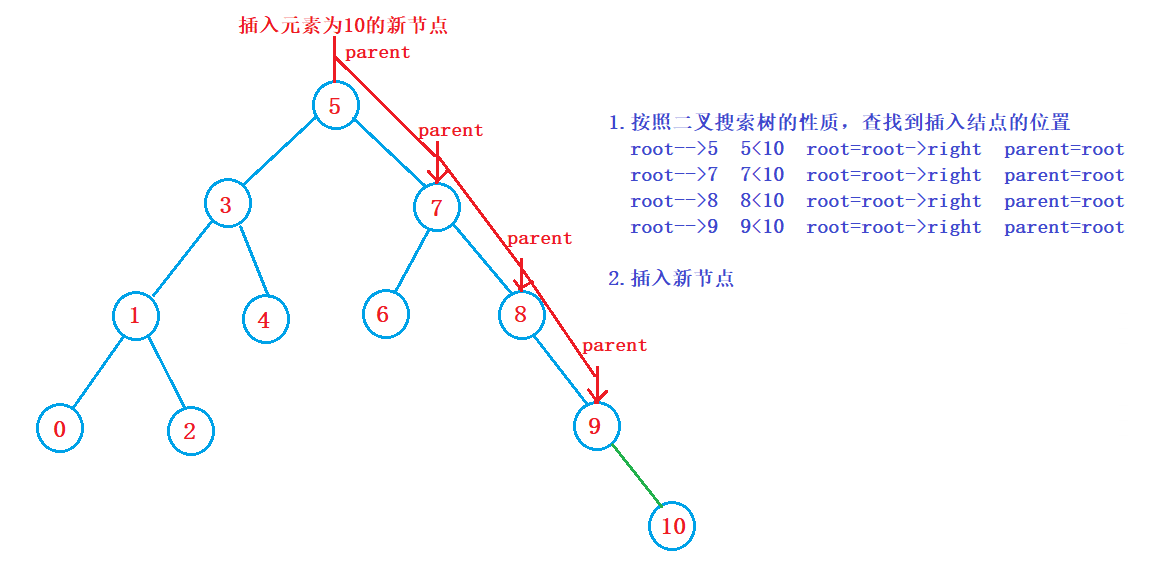
Iteration:
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//Find the location to insert
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < cur->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Recursion:
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
else
{
if (root->_key < key)
{
return _InsertR(root->_left, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
}
delete
First, check whether the element is in the binary search tree. If it does not exist, it will be returned. Otherwise, the nodes to be deleted may be divided into the following four cases:
- The node to be deleted has no children
- Only the left child node is to be deleted
- The node to be deleted has only the right child node
- The nodes to be deleted are only left and right nodes
In practice, 1 and 2 or 3 can be merged, so the real deletion process is as follows:
- Delete the node and make the parent node of the deleted node point to the left child node of the deleted node
- Delete the node and make the parent node of the deleted node point to the right child node of the deleted node
- Substitution method. In its right subtree, find the first node in the middle order (the smallest key code), fill its value into the deleted node, and then deal with the deletion of the node.
Iteration:
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//delete
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else
{
//Find the smallest node in the right tree to replace the deletion
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRight == minRightParent->_left)
minRightParent->_left = minRight->_right;
else
minRightParent->_right = minRight->_right;
delete minRight;
}
return true;
}
}
return false;
}
Recursion:
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
//delete
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
//Substitution deletion
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
root->_key = minRight->_key;
//Convert to recursion and delete the smallest node in the right subtree
return _EraseR(root->_right, minRight->_key);
}
delete del;
return true;
}
}
Application of binary search tree
1.K model: in the K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched. For example: give a word word and judge whether the word is spelled correctly. The specific methods are as follows: 1 Take each word in the word set as the key to build a binary search tree. 2. Retrieve whether the word exists in the binary search tree. If it exists, it is spelled correctly, and if it does not exist, it is spelled incorrectly.
2.KV model: each key has its corresponding Value value, that is, the key Value pair of < key, Value >. This method is very common in real life: for example, an English Chinese dictionary is the corresponding relationship between English and Chinese. The corresponding Chinese can be quickly found through English, and the English word and its corresponding Chinese < word, Chinese > constitute a key Value pair; Another example is to count the number of words. After successful statistics, the number of occurrences of a given word can be quickly found. The word and its number of occurrences are < word, count > to form a key Value pair.
For example: to implement a simple English Chinese Dictionary dict, you can find its corresponding Chinese in English. The specific implementation methods are as follows: 1< Construct a binary search tree for Key value pairs. Note: the binary search tree needs to be compared. When comparing Key value pairs, only Key is compared. 2. When querying English words, you only need to give the English words to quickly find the corresponding Key.
namespace KEY_VALUE {
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
,_right(nullptr)
,_key(key)
,_value(value)
{}
};
template<class K, class V>
class BSTree {
typedef BSTreeNode<K, V> Node;
public:
V& operator[](const K& key)
{
pair<Node*, bool> ret = Insert(key, V());
return ret.first->_value;
}
pair<Node*, bool> Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return make_pair(_root, true);
}
//Find the location to insert
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(key, value);
if (parent->_key < cur->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return make_pair(cur, true);
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//delete
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else
{
//Find the smallest node of the right tree to replace the deletion
Node* minRightParent = cur;
Node* minRight = cur->_left;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRight = minRightParent->_left)
minRightParent->_left = minRight->right;
else
minRightParent->_right = minRight->_right;
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
}
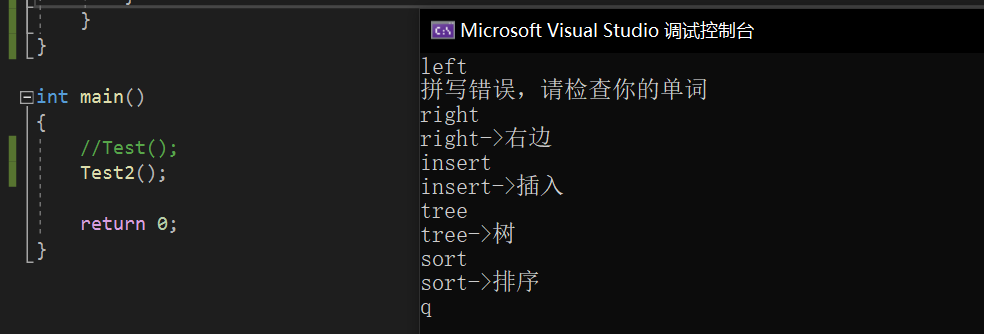
void Test2()
{
KEY_VALUE::BSTree<string, string> dict;
dict.Insert("sort", "sort");
dict.Insert("insert", "insert");
dict.Insert("tree", "tree");
dict.Insert("right", "right");
string str;
while (cin >> str)
{
if (str == "q")
{
break;
}
else
{
auto ret = dict.Find(str);
if (ret == nullptr)
{
cout << "Spelling error, please check your words" << endl;
}
else
{
cout << ret->_key <<"->"<< ret->_value << endl;
}
}
}
}
void Test3()
{
//Counts the number of occurrences of a string. It is also a classic key/value
string str[] = { "sort", "sort", "tree", "insert", "sort", "tree", "sort", "test", "sort" };
KEY_VALUE::BSTree<string, int> countTree;
//for (auto& e : str)
//{
// auto ret = countTree.Find(e);
// if (ret == nullptr)
// {
// countTree.Insert(e, 1);
// }
// else
// {
// ret->_value++;
// }
//}
for (auto& e : str)
{
countTree[e]++;
}
countTree.InOrder();
}
Performance analysis of binary tree
Insert and delete operations must be searched first. The search efficiency represents the performance of each operation in the binary search tree.
For a binary search tree with n nodes, if the search probability of each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the deeper the node, the more times of comparison.
However, for the same key set, if the key insertion order is different, binary search trees with different structures may be obtained
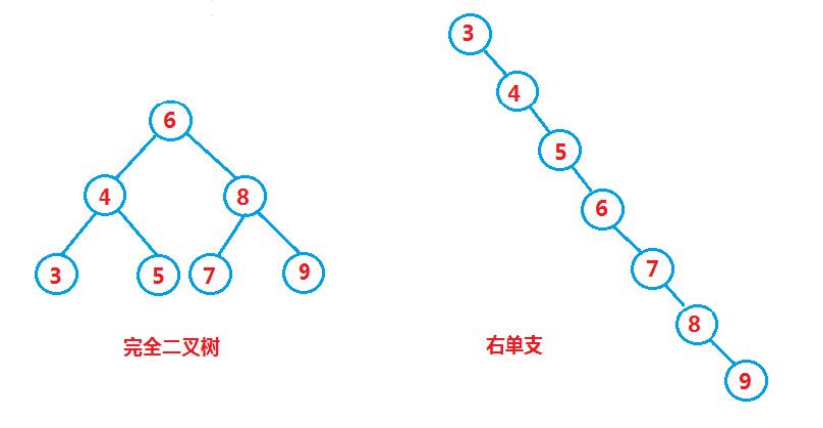
In the optimal case, the binary search tree is a complete binary tree, and its average comparison times is: logN
In the worst case, the binary search tree degenerates into a single branch tree, and its average comparison times is N/2