Binary search tree concept
Binary search tree, also known as binary sort tree, is either an empty tree or a binary tree with the following properties:
- If its left subtree is not empty, the value of all nodes on the left subtree is less than that of the root node
- If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of the root node
- Its left and right subtrees are also binary search trees
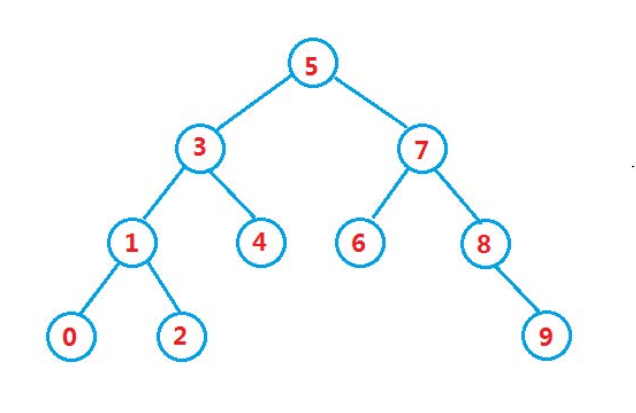
int a [] = {5,3,4,1,7,8,2,6,0,9};
Carefully observe the search binary tree. Its middle order traversal actually constitutes an ascending sort, so the binary search tree is also called binary sort tree
Binary search tree operation
-
Search of binary search tree
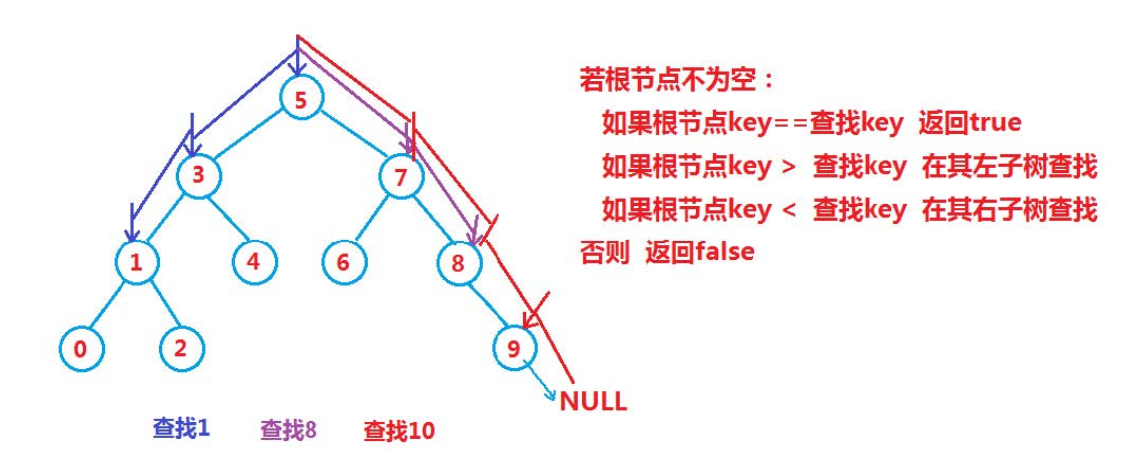
-
Insertion of binary search tree
The specific process of inserting is as follows:-
If the tree is empty, insert it directly

-
If the tree is not empty, find the insertion position according to the nature of binary search tree and insert a new node
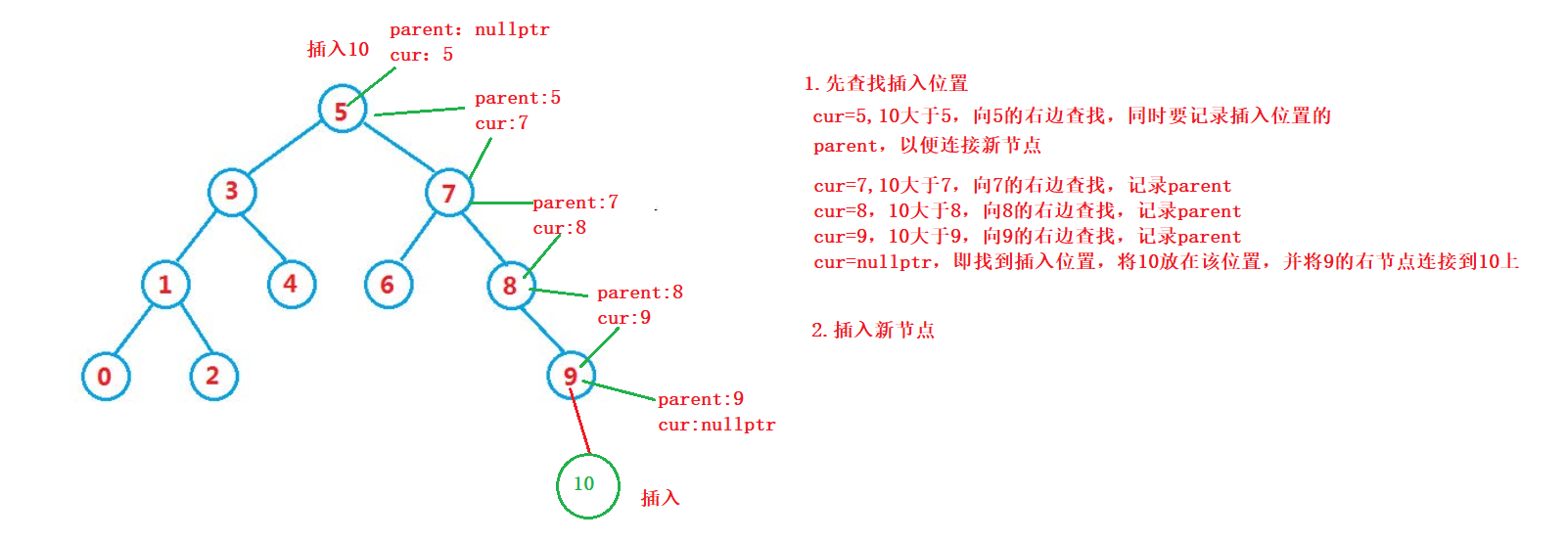
-
-
Deletion of binary search tree
First, check whether the element is in the binary search tree. If it does not exist, it will be returned. Otherwise, the nodes to be deleted may be divided into the following four cases:- The node to be deleted has no child nodes (i.e. leaf nodes)
- Only the left child node is to be deleted
- The node to be deleted has only the right child node
- The nodes to be deleted include left and right child nodes
It seems that there are four kinds of nodes to be deleted. The actual situation a can be combined with situation b or c. Therefore, the real deletion process is as follows:
- Case b: delete the node and make the parent node of the deleted node point to the left child node of the deleted node
- Case c: delete the node and make the parent node of the deleted node point to the right child node of the deleted node
- Case d: find the first node in the middle order in its right subtree (the smallest key), fill it with its value to the deleted node, and then deal with the deletion of the node
Implementation of binary search tree
//Node creation
template<class T>
struct BSTNode {//Binary Search Tree
BSTNode* _left;
BSTNode* _right;
T _val;
//structure
BSTNode(const T& val = T())
:_left(nullptr)
,_right(nullptr)
,_val(val)
{}
};
//Implementation of search tree
template<class T>
class BSTree {
typedef BSTNode<T> node;
typedef BSTNode<T>* pnode;
private:
pnode root = nullptr;
public:
BSTree()
: root(nullptr)
{}
void _Destroy(pnode node)
{
if (node == nullptr)
return;
_Destroy(node->_left);
_Destroy(node->_right);
delete node;
node = nullptr;
}
~BSTree()
{
_Destroy(root);
}
//Air judgment
bool empty()
{
return root == nullptr;
}
//insert
//If there is no such element in the tree, insert it and return true
//If the element already exists in the tree, it will not be inserted and false will be returned
bool insert(const T& val)
{
//Insert directly when the tree is empty
if (root == nullptr)
{
root = new node(val);
return true;
}
pnode parent = nullptr;
pnode cur = root;
while (cur)
{
//Find the insertion position to the left
if (val < cur->_val)
{
parent = cur;
cur = cur->_left;
}
else if (val > cur->_val)//Find the insertion position to the left
{
parent = cur;
cur = cur->_right;
}
else//This value already exists, no need to insert
{
return false;
}
}
//Insert when found
cur = new node(val);
//Determine whether it is inserted in the left node or the right node
if (parent->_val > val)//Put it on the left
{
parent->_left = cur;
}
else//On the right
{
parent->_right = cur;
}
return true;
}
void _order(pnode& root)
{
if (root == nullptr)
return;
_order(root->_left);
cout << root->_val << " ";
_order(root->_right);
}
//Middle order traversal
void order()
{
_order(root);
cout << endl;
}
//lookup
bool find(const T& val)
{
pnode cur = root;
while (cur)
{
//Look to the left
if (cur->_val > val)
{
cur = cur->_left;
}
else if (cur->_val < val)//Look to the right
{
cur = cur->_right;
}
else//eureka
{
return true;
}
}
return false;
}
//Delete node
bool erase(const T& val)
{
assert(!empty());
pnode cur = root;
pnode parent = nullptr;
//Find the node first
while (cur)
{
if (cur->_val > val)//Look to the left
{
parent = cur;
cur = cur->_left;
}
else if (cur->_val < val)//Look to the right
{
parent = cur;
cur = cur->_right;
}
else//eureka
{
//Judge whether the left and right subtrees are empty
//1. The left subtree is empty, and the parent is connected to its right subtree
//2. The right subtree is empty, and the parent is connected to its left subtree
//3. The left and right subtrees are not empty. Replace and delete them
if (cur->_left == nullptr)
{
if (cur == root)//If the root node is deleted and the left tree is empty, the right node will become the root directly
{
root = root->_right;
}
else
{
//Judge whether cur is the left node or the right node of the parent
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == root)//If the root node is deleted and the right tree is empty, the left node will become the root directly
{
root = root->_left;
}
else
{
//Judge whether cur is the left node or the right node of the parent
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//The left and right subtrees are not empty
{
//Find the smallest node to the right and replace it
pnode RightMin = cur->_right;
pnode RightMinParent = cur;
//Keep looking to the left
while (RightMin->_left)
{
RightMinParent = RightMin;
RightMin = RightMin->_left;
}
//When found, replace the value with the value of cur
cur->_val = RightMin->_val;
//Connect the right subtree of the replacement node to the left subtree or right subtree of the parent of the replacement node
//Determine which node of the Parent the MIn is
if (RightMinParent->_left == RightMin)
{
RightMinParent->_left = RightMin->_right;
}
else
{
RightMinParent->_right = RightMin->_right;
}
delete RightMin;
}
return true;
}
}
return false;//Can't find
}
};
When deleting a node whose left and right nodes are not empty, the right subtree of the replacement node may not be connected to the right node of its parent node. For example, delete 7 and find 8 as the smallest node of the right subtree. 7 is its parent node, and the right subtree of 8 should be connected to the right of 7, not the left. Therefore, before connecting the right subtree of the replacement node, it is necessary to judge whether it is connected to the left or right of its parent node
There is a problem with deleting 7 first
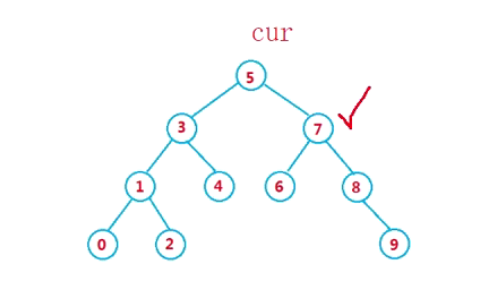
When there is only one node, the deletion will reference the parent, so that the left and right subtrees of the deleted node are connected to the left or right of the parent. At this time, the parent is empty, and it is illegal to access its left and right subtrees. Therefore, it is necessary to make special judgment on the tree with only one node.
Application of binary search tree
-
K model: in K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched.
For example, give a word word and judge whether the word is spelled correctly. The specific methods are as follows:- Take each word in the word set as the key to build a binary search tree
- Retrieve whether the word exists in the binary search tree. If it exists, it will be spelled correctly, and if it does not exist, it will be misspelled.
-
KV model: each key has its corresponding Value value, that is, the key Value pair of < key, Value >. This method is very common in real life: for example, an English Chinese dictionary is the corresponding relationship between English and Chinese. The corresponding Chinese can be quickly found through English, and the English word and its corresponding Chinese < word, Chinese > constitute a key Value pair; Another example is to count the number of words. After successful statistics, the number of occurrences of a given word can be quickly found. The word and its number of occurrences are < word, count > to form a key Value pair. For example, a simple English Chinese Dictionary dict is implemented, and the corresponding Chinese can be found in English. The specific implementation methods are as follows:
-
< word, Chinese meaning > constructs a binary search tree for Key value pairs. Note: the binary search tree needs to be compared. When comparing Key value pairs, only Key is compared
-
When querying English words, you can quickly find the corresponding key by giving the English words
//Node creation template<class K,class V> struct BSTNode {//Binary Search Tree BSTNode* _left; BSTNode* _right; K _key; V _val; //structure BSTNode(const K& key = K(), const V& val = V()) :_left(nullptr) , _right(nullptr) ,_key(key) , _val(val) {} }; //Implementation of search tree template<class K, class V> class BSTree { typedef BSTNode<K, V> node; typedef BSTNode<K, V>* pnode; private: pnode root = nullptr; public: BSTree() : root(nullptr) {} void _Destroy(pnode node) { if (node == nullptr) return; _Destroy(node->_left); _Destroy(node->_right); delete node; node = nullptr; } ~BSTree() { _Destroy(root); } //Air judgment bool empty() { return root == nullptr; } //insert //If there is no such element in the tree, insert it and return true //If the element already exists in the tree, it will not be inserted and false will be returned bool insert(const K& key, const V& val) { //Insert directly when the tree is empty if (root == nullptr) { root = new node(key, val); return true; } pnode parent = nullptr; pnode cur = root; while (cur) { //Find the insertion position to the left if (key < cur->_key) { parent = cur; cur = cur->_left; } else if (key > cur->_key)//Find the insertion position to the left { parent = cur; cur = cur->_right; } else//This value already exists, no need to insert { return false; } } //Insert when found cur = new node(key, val); //Determine whether it is inserted in the left node or the right node if (parent->_key > key)//Put it on the left { parent->_left = cur; } else//On the right { parent->_right = cur; } return true; } void _order(pnode& root) { if (root == nullptr) return; _order(root->_left); cout << root->_key << "->" << root->_val <<endl; _order(root->_right); } //Middle order traversal void order() { _order(root); cout << endl; } //lookup pnode find(const K& key) { pnode cur = root; while (cur) { //Look to the left if (cur->_key > key) { cur = cur->_left; } else if (cur->_key < key)//Look to the right { cur = cur->_right; } else//eureka { return cur; } } return nullptr; } //Delete node bool erase(const K& key) { assert(!empty()); pnode cur = root; pnode parent = nullptr; //Find the node first while (cur) { if (cur->_key > key)//Look to the left { parent = cur; cur = cur->_left; } else if (cur->_key < key)//Look to the right { parent = cur; cur = cur->_right; } else//eureka { //Judge whether the left and right subtrees are empty //1. The left subtree is empty, and the parent is connected to its right subtree //2. The right subtree is empty, and the parent is connected to its left subtree //3. The left and right subtrees are not empty. Replace and delete them if (cur->_left == nullptr) { if (cur == root)//If the root node is deleted and the left tree is empty, the right node will become the root directly { root = root->_right; } else { //Judge whether cur is the left node or the right node of the parent if (parent->_left == cur) { parent->_left = cur->_right; } else { parent->_right = cur->_right; } } delete cur; } else if (cur->_right == nullptr) { if (cur == root)//If the root node is deleted and the right tree is empty, the left node will become the root directly { root = root->_left; } else { //Judge whether cur is the left node or the right node of the parent if (parent->_left == cur) { parent->_left = cur->_left; } else { parent->_right = cur->_left; } } delete cur; } else//The left and right subtrees are not empty { //Find the smallest node to the right and replace it pnode RightMin = cur->_right; pnode RightMinParent = cur; //Keep looking to the left while (RightMin->_left) { RightMinParent = RightMin; RightMin = RightMin->_left; } //When found, replace the value with the value of cur cur->_key = RightMin->_key; cur->_val = RightMin->_val; //Connect the right subtree of the replacement node to the left subtree or right subtree of the parent of the replacement node //Determine which node of the Parent the MIn is if (RightMinParent->_left == RightMin) { RightMinParent->_left = RightMin->_right; } else { RightMinParent->_right = RightMin->_right; } delete RightMin; } return true; } } return false;//Can't find } };
-
Dictionary test
//Dictionary test
void TestDic()
{
BSTree<string, string> bst;
bst.insert("hello", "Hello");
bst.insert("goodbye", "bye");
bst.insert("kobe", "Kobe");
bst.insert("buy", "buy");
bst.insert("insert", "insert");
bst.insert("sort", "sort");
bst.insert("tree", "tree");
bst.order();
auto result = bst.find("kobe");
cout << result->_key << "->" << result->_val << endl << endl;
bst.erase("hello");
bst.erase("goodbye");
bst.erase("sort");
bst.erase("tree");
bst.erase("buy");
bst.order();
}
Count the number of occurrences of names in the array
//Count the number of student names in the array
void TestCountName()
{
BSTree<string, int> bst;//int counts the number of occurrences
const char* arr[] = {"Zhang San", "Li Si", "Wang Wu", "Zhao Liu","Zhang San", "Zhang San", "Zhang San", "Li Si" ,"Li Si" ,"Zhao Liu" };
for (auto e : arr)
{
BSTNode<string, int>* ret = bst.find(e);
//The name is not in the tree
if (ret == nullptr)
bst.insert(e, 1);//Set the number of occurrences to 1
else//It has already appeared
bst.insert(e, ret->_val++);
}
bst.order();
}
Performance analysis of binary search tree
Insert and delete operations must be searched first. The search efficiency represents the performance of each operation in the binary search tree.
The deeper the search probability of each node in the binary tree is, the deeper the search probability of each node in the binary tree is, the more the search probability of each node in the binary tree is.
However, for the same key set, if the insertion order of each key is different, binary search trees with different structures may be obtained:
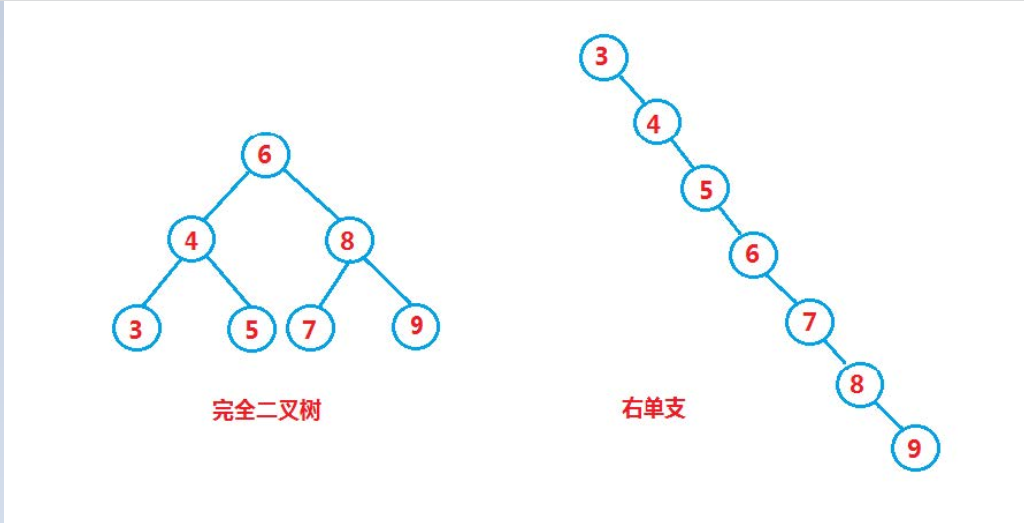
In the optimal case, the binary search tree is a complete binary tree, and its average comparison times is log2(N)
In the worst case, the binary search tree degenerates into a single branch tree, and its average comparison times is N/2
Problem: if it degenerates into a single tree, the performance of binary search tree will be lost. Can we improve it? No matter what order the key is inserted, it can be the best performance of binary search tree?
Solve - > AVL tree and red black tree with balanced tree