Binary sort tree of data structure (C + + implementation)

Binary tree is a very, very important part of data structure. As the saying goes, if you don't know the Great Wall, you don't know the data structure. What is a binary tree? We have learned about the linked list before, but when we use it, we will find a problem that each node of the linked list can only point to one node in the same direction, that is, it can not be forked. However, forks must exist in practical application. What should we do? Predecessors put forward the concept of binary sort tree. Through the previous study, we learned that the single linked list has two areas, namely, the data field and the pointer field. In order to realize reverse traversal, the two-way linked list adds an additional area called the precursor pointer field, so the two-way linked list has three fields, the precursor pointer field, the successor pointer field and the data field. Similarly, we can guess that the binary tree adds another field, so there are four fields, That is, parent pointer field, data field, left subtree pointer field and right subtree pointer field. Let's take a closer look at the figure below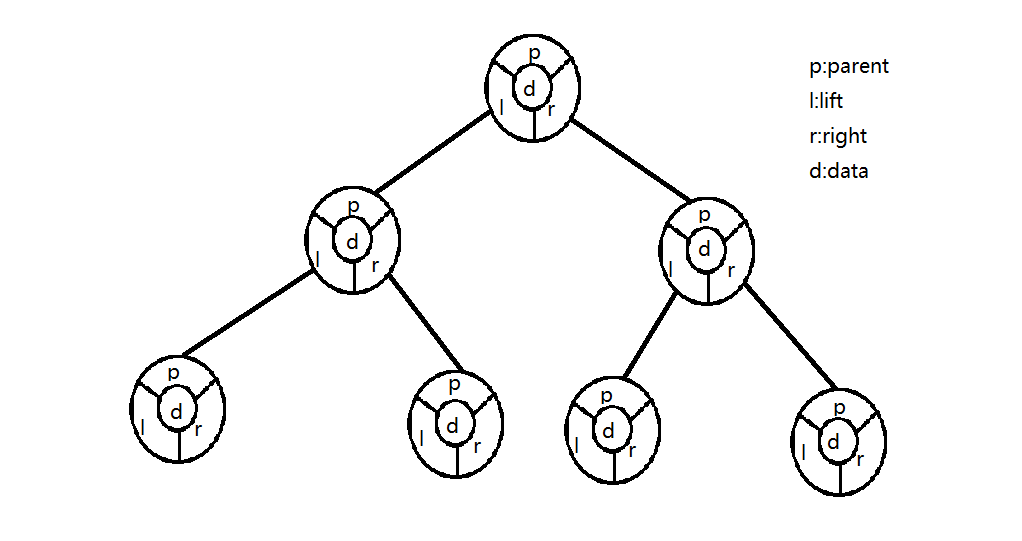

In order to facilitate understanding, I marked up the four areas of the sorting tree. Through the previous study, we can understand that when we use the resume binary sorting tree, we need to establish a node class. The attributes of the class should have four points, that is, the four points in the figure, P, l, R and D. Then, we form a tree class together through node classes, so we need to create a tree class. Then there are no attributes in the generic class, because its attributes are the attributes of nodes, so the behavior of the tree is the operation on the tree, that is, the operation of adding, deleting, modifying and querying. Let's explain it in detail in the code below.

class node
{
public:
	int data;
	node *parent;
	node *lift;
	node *right;
	node() : data(-1) , parent(NULL) , lift(NULL) , right(NULL) {}
	node(int num) : data(num) , parent(NULL) , lift(NULL) , right(NULL) {}
};

The code above is the class of the node we established. We established four regions of the node and two constructors, that is, when we established a node, we created a node with four regions, and passed parameters to its data domain through the constructor. For node classes, each node has two downward pointers and one upward pointer.

class trees
{
public:
	trees(int num[] , int len);		//Constructor to insert n data
	void insertnode(int data);		//Non recursive method
	void insertnode1(int data);		//Recursive method
	node *searchnode(int data);		//Find node
	void deletenode(int data);		//Delete node and its subtree
	void inorder();					//Medium order traversal
private:
	void insertnode(node* cur , int data);	//Recursive insertion
	node *searchnode(node* cur , int data); //recursive lookup 
	void deletenode(node* cur);				//Recursive deletion
	void inorder(node* cur);				//Recursive middle order traversal
	node* root;								//Root node of binary sort tree
};

The code here is the class and constructor of our tree. We use the array method to create a binary tree. We all know that there are two methods to create a binary tree, namely recursive method and non recursive method. Therefore, in my last blog post, I told you what recursion is, and gave an example by using the code of Hanoi tower, And the search and deletion method below also uses the recursive method.

Non recursive method:

We first create a binary tree by using a non recursive method. The specific code is as follows:

trees::trees(int num[] , int len)
{
	root = new node(num[0]);
	
	for(int i = 1; i<len; i++)
	{
		insertnode1(num[i]);
	}
}
/*Above this is the constructor of the tree class. We pass a loop to all the data in the array
 Write to the binary tree. Here, the non recursive method is used first*/
void trees::insertnode1(int datanew)
{
	node *p , *par;
	node *newnode = new node(datanew);
	p = par = root;
	while(p != NULL)
	{
		par = p;
		if(datanew > p->data)
		{
			p = p->right;
		}
		else if(datanew < p->data)
		{
			p = p-> lift;
		}
		else if(datanew == p->data)
		{
			delete newnode;
			return;
		}
	}
	newnode->parent = par;
	if(par->data > newnode->data)
	{
		par->lift = newnode;
	}
	else
	{
		par->right = newnode;
	}
		
}
/*This function is mainly composed of two parts. One part is to find when inserting a
 When a new node, the program should know where to insert it, because it is binary
 Sorting tree, why is it called binary sorting tree, because the value of the left subtree is always higher than that of the left subtree
 The right subtree is small, and the data of the root node must be larger than that of the left subtree and smaller than that of the right subtree.*/

The above code is that we create a binary tree and insert data into it. It is divided into the following steps in detail:

1. Create a node, that is, node *newnode = new node(int);

2. Find the specific location of the new node

According to the nature of the binary tree, you need to traverse when inserting data into the binary tree. If you find a node with the same data, the new node will have no meaning of existence, so you delete it.

3. Insert operation after location is found.

The above is a non recursive method of inserting nodes. Let's explain the recursive method.

Recursive method:

I won't say more about recursion. To understand, look at my last blog post. I actually wrote an insertion method for inserting nodes by recursive method, but I wrote the specific insertion operation in the insertnode method of private behavior. The specific code is as follows:

//Recursive method
void trees::insertnode(int data)
{
	if(root != NULL)
	{
		insertnode(root , data);			//Call the method of recursive insertion
	}
}
void trees::insertnode(node* cur , int data)
{
	//First, check the size of the inserted data and the data of the current node
	if(data < cur->data)
	{
		if(cur->lift == NULL)
		{
			cur->lift = new node(data);
			cur->lift->parent = cur;
		}
		else
		{
			insertnode(cur->lift , data);	//Here we enter recursion, because the left subtree of a node is also a binary tree
		}
	}
	else if(data>cur->data)
	{
		if(cur->right == NULL)
		{
			cur->right = new node(data);
			cur->right->parent = cur;
		}
		else
		{
			insertnode(cur->right , data);
		}
	}
	return;
}

Looking at the code above, many people may not understand how a recursive call is. I can explain it with a diagram

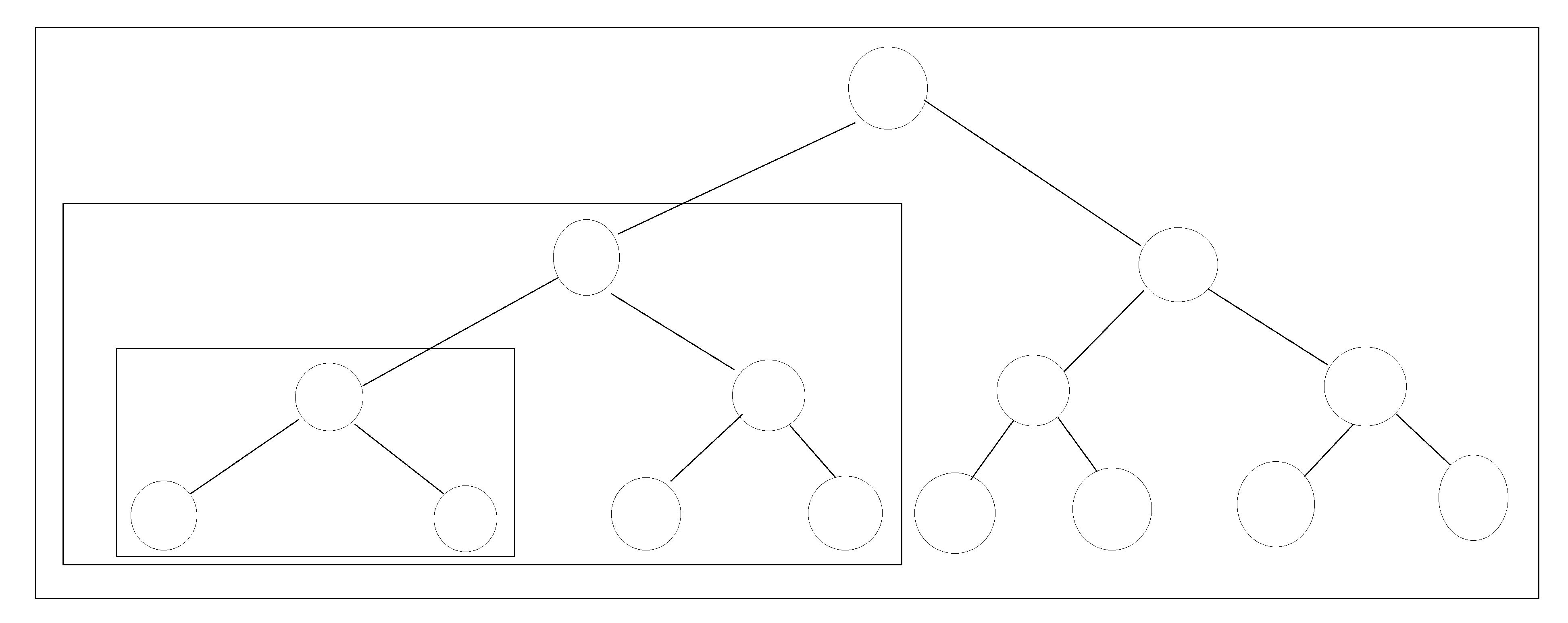
As shown in the figure, each box can be regarded as a binary tree, that is, all operations on the binary tree can be carried out, so there is a recursive method to operate. Then we explain the steps executed by the function insertnode of the private attribute:

1. If the data value of the current node is less than data, we should insert it in its left sub tree. At this time, we have a judgment, that is, if the current node has no left sub node, we will take the inserted new node as its left sub node. Otherwise, its left sub node will be compared with data and continue until the end of.

2. If the data value of the current node is greater than data, it is actually similar to the first step, that is, one left and one right, one large and one small. I don't talk much nonsense, mainly lazy.

Let's take a look at the search method in the binary tree:

Recursive lookup:

Through the above code and the previous blog, we learned that the use of recursive algorithm can make our code simpler and the code is no longer redundant. Then our search is also written by recursive method. The code is as follows:

//Here's a look
node* trees::searchnode(int data)
{
	
	node * p = new node(data);
	if(root != NULL)
	{
		p = searchnode(root , data);
		return p;
	}
	return NULL;
}
node* trees::searchnode(node* cur , int data)
{
	if(data < cur->data)
	{
		if(cur->lift == NULL)
		{
			return NULL;
		}
		return searchnode(cur->lift , data);
	}
	else if(data>cur->data)
	{
		if(cur->right == NULL)
		{
			return NULL;
		}
		return searchnode(cur->right , data);
	}
	return cur;
}

From the above code, we can conclude that the search process of binary sort tree can be divided into the following steps:

1. If the data is less than the current cur value and the left subtree of cur exists, continue to search the left subtree of cur, otherwise NULL is returned;

2. If data is greater than the current value of cur and the right subtree of cur exists, continue to search the right subtree of cur, otherwise NULL is returned;

3. If data is equal to the value of the current node, cur is returned.

Delete node

In actual work, we often encounter the situation of deleting data in the star tree, so we must have a complete algorithm to realize the deletion operation. Of course, I directly delete the tree after locating the node. I think it's OK to delete a data, but I didn't write it when I wrote my code, Because it is too troublesome to compare the size and reorder again, let's directly show you the code for deleting the tree

//The following is the deletion
void trees::deletenode(int data)
{
	node* cur = new node(data);
	cur = searchnode(data);
	if(cur != NULL)
	{
		deletenode(cur);
	}
}

void trees::deletenode(node *cur)
{
	if(cur->lift != NULL)
	{
		deletenode(cur->lift);
	}
	if(cur->right != NULL)
	{
		deletenode(cur->right);
	}
	if(cur->parent == NULL)
	{
		delete cur;
		root = NULL;
		return;
	}
	if(cur->parent->data > cur->data)
	{
		cur->parent->lift = NULL;
	}
	else
	{
		cur->parent->right = NULL;
	}
	delete cur;
}

I will explain the above code here as follows:

The public member method deletenode() deletes the node and its subtree whose data is data. First, the searchnode() method is called to find the location of the node we need to delete. If it is found, the private member method searchnode() will be called to return.

The private member method also uses the recursive method to delete. The specific methods are as follows

1. If the cur left subtree exists, the left subtree is deleted recursively;

2. If its right subtree exists, the right subtree is deleted recursively;

3. If the bold person is deleted at last, and cur is the root node, you need to set root to null. Otherwise, set the pointer corresponding to its parent node to null.

So far, the first mountain of our binary tree, the "entry mountain", has been turned over. We can write a print function to print. Like the linked list, if you want to print, you must traverse. The traversal method in the binary tree will be introduced in detail in my next blog. Here, you can directly use the middle order traversal.

Middle order traversal:

This paragraph doesn't need to be understood. In fact, it's very simple. I'll explain it in detail in the next blog

//Medium order traversal
void trees::inorder()
{
	if(root == NULL)
	{
		return;
	}
	inorder(root);
}
void trees::inorder(node* cur)
{
	if(cur != NULL)
	{
		inorder(cur->lift);
		cout<<cur->data<<" ";
		inorder(cur->right);
	}
}

OK, that's almost finished. Let's add the main function to see the effect of operation:

int main()
{
	int num[] = {5,3,1,4,8,9,7,6,2,11,34,99,100};
	trees tr(num , 13);
	tr.inorder();
	cout << endl;
	tr.insertnode(78);
	tr.inorder();
	cout << endl;
	tr.deletenode(11);
	tr.inorder();
	return 0;
}

ok, today's binary tree will be introduced here first. In the next blog, we will talk about several sorting methods of binary tree, and finally post our engineering code for reference. If you have any questions, you are welcome to leave a message or private letter for discussion

//main.cpp

#include "tree.h"
int main()
{
	int num[] = {5,3,1,4,8,9,7,6,2,11,34,99,100};
	trees tr(num , 13);
	tr.inorder();
	cout << endl;
	tr.insertnode(78);
	tr.inorder();
	cout << endl;
	tr.deletenode(11);
	tr.inorder();
	return 0;
}

//tree.h

#ifndef _TREE_H_
#define _TREE_H_

#include <iostream>
using namespace std;

class node
{
public:
	int data;
	node *parent;
	node *lift;
	node *right;
	node() : data(-1) , parent(NULL) , lift(NULL) , right(NULL) {}
	node(int num) : data(num) , parent(NULL) , lift(NULL) , right(NULL) {}
};

class trees
{
public:
	trees(int num[] , int len);		//Constructor to insert n data
	void insertnode(int data);		//Non recursive method
	void insertnode1(int data);		//Recursive method
	node *searchnode(int data);		//Find node
	void deletenode(int data);		//Delete node and its subtree
	void inorder();					//Medium order traversal
private:
	void insertnode(node* cur , int data);	//Recursive insertion
	node *searchnode(node* cur , int data); //recursive lookup 
	void deletenode(node* cur);				//Recursive deletion
	void inorder(node* cur);				//Recursive middle order traversal
	node* root;								//Root node of binary sort tree
};

#endif

//tree.cpp

#include "tree.h"

trees::trees(int num[] , int len)
{
	root = new node(num[0]);
	
	for(int i = 1; i<len; i++)
	{
		insertnode1(num[i]);
	}
}

void trees::insertnode1(int datanew)
{
	node *p , *par;
	node *newnode = new node(datanew);
	p = par = root;
	while(p != NULL)
	{
		par = p;
		if(datanew > p->data)
		{
			p = p->right;
		}
		else if(datanew < p->data)
		{
			p = p-> lift;
		}
		else if(datanew == p->data)
		{
			delete newnode;
			return;
		}
	}
	newnode->parent = par;
	if(par->data > newnode->data)
	{
		par->lift = newnode;
	}
	else
	{
		par->right = newnode;
	}
}

//Recursive method
void trees::insertnode(int data)
{
	if(root != NULL)
	{
		insertnode(root , data);			//Call the method of recursive insertion
	}
}
void trees::insertnode(node* cur , int data)
{
	//First, check the size of the inserted data and the data of the current node
	if(data < cur->data)
	{
		if(cur->lift == NULL)
		{
			cur->lift = new node(data);
			cur->lift->parent = cur;
		}
		else
		{
			insertnode(cur->lift , data);	//Here we enter recursion, because the left subtree of a node is also a binary tree
		}
	}
	else if(data>cur->data)
	{
		if(cur->right == NULL)
		{
			cur->right = new node(data);
			cur->right->parent = cur;
		}
		else
		{
			insertnode(cur->right , data);
		}
	}
	return;
}

//Here's a look
node* trees::searchnode(int data)
{
	node *p = new node(data);
	if(root != NULL)
	{
		p = searchnode(root , data);
		return p;
	}
	return NULL;
}
node* trees::searchnode(node* cur , int data)
{
	if(data < cur->data)
	{
		if(cur->lift == NULL)
		{
			return NULL;
		}
		return searchnode(cur->lift , data);
	}
	else if(data>cur->data)
	{
		if(cur->right == NULL)
		{
			return NULL;
		}
		return searchnode(cur->right , data);
	}
	return cur;
}

//The following is the deletion
void trees::deletenode(int data)
{
	node* cur = new node(data);
	cur = searchnode(data);
	if(cur != NULL)
	{
		deletenode(cur);
	}
}

void trees::deletenode(node *cur)
{
	if(cur->lift != NULL)
	{
		deletenode(cur->lift);
	}
	if(cur->right != NULL)
	{
		deletenode(cur->right);
	}
	if(cur->parent == NULL)
	{
		delete cur;
		root = NULL;
		return;
	}
	if(cur->parent->data > cur->data)
	{
		cur->parent->lift = NULL;
	}
	else
	{
		cur->parent->right = NULL;
	}
	delete cur;
}

//Medium order traversal
void trees::inorder()
{
	if(root == NULL)
	{
		return;
	}
	inorder(root);
}
void trees::inorder(node* cur)
{
	if(cur != NULL)
	{
		inorder(cur->lift);
		cout<<cur->data<<" ";
		inorder(cur->right);
	}
}

Keywords: Algorithm data structure Binary tree

Added by mfouts on Sun, 21 Nov 2021 05:43:43 +0200

Programming VIP