1. Find the minimum depth of binary tree
First, understand the concept of minimum depth: minimum depth is the number of nodes on the shortest path from the root node to the nearest leaf node., Note the leaf node.
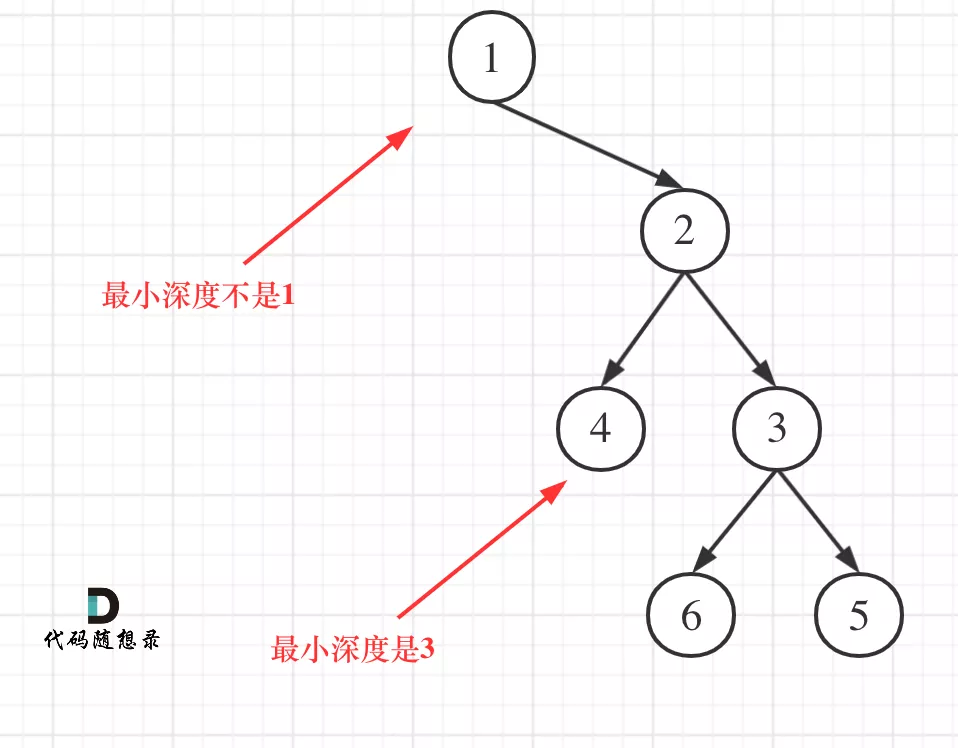
If so, the branch without left child will be regarded as the shortest depth.
Therefore, if the left subtree is empty and the right subtree is not empty, the minimum depth is 1 + the depth of the right subtree.
The depth of the left subtree is not empty, and the depth of the right subtree is not empty. On the contrary, the depth of the left subtree is not empty. Finally, if the left and right subtrees are not empty, return the minimum depth of the left and right subtrees + 1.
class Solution {
public:
//Recursive method
int getdepth(TreeNode* cur)
{
if(cur==NULL) return 0;
int minleft=getdepth(cur->left);
int minright=getdepth(cur->right);
if(cur->left && cur->right)
{
return min(minleft,minright)+1;
}
else if(!cur->left && cur->right)
{
return minright+1;
}
return minleft+1;
}
int minDepth(TreeNode* root) {
if(root==NULL) return 0;
return getdepth(root);
}
};
2. Given a binary tree, judge whether it is a highly balanced binary tree.
In this question, a highly balanced binary tree is defined as:
The absolute value of the height difference between the left and right subtrees of each node of a binary tree shall not exceed 1.
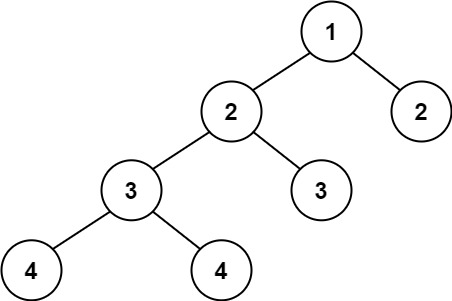
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false
A wave of concepts is emphasized here:
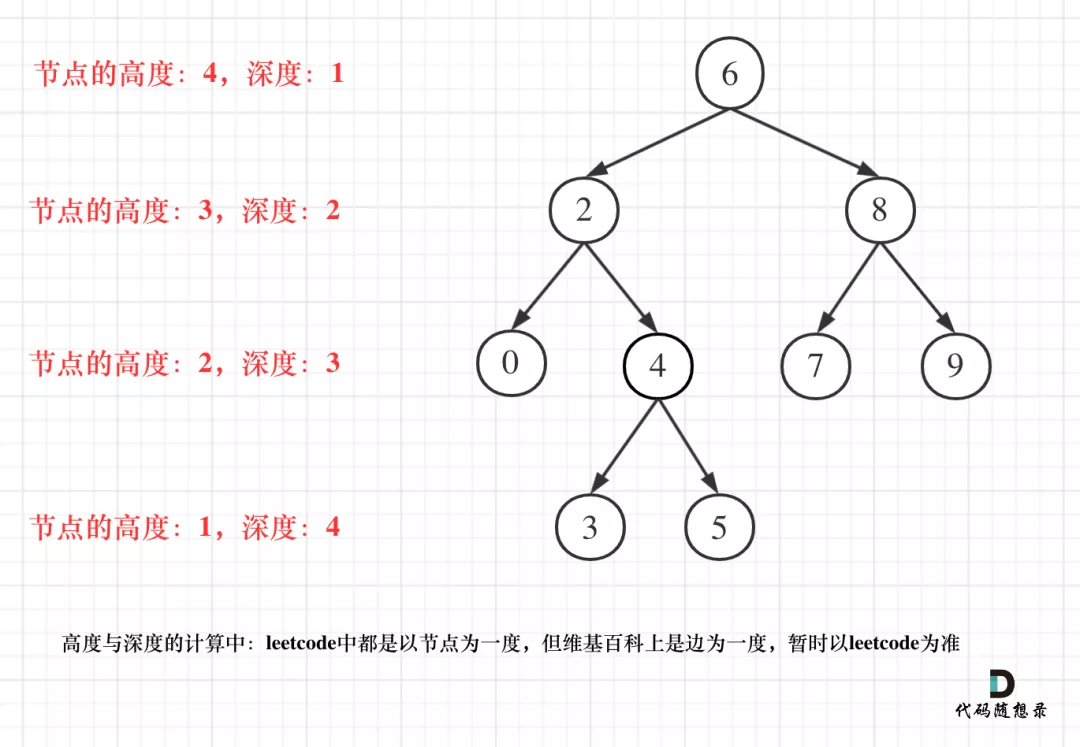
Depth of binary tree node: refers to the number of edges of the longest simple path from the root node to the node.
Height of binary tree node: refers to the number of edges of the longest simple path from this node to the leaf node.
class Solution {
public:
// -1 indicates that it is not a balanced binary tree, otherwise the return value is the height of the tree with this node as the root node
int height(TreeNode* cur)
{
if(cur==NULL) return 0;
int lheight=height(cur->left);
int rheight=height(cur->right);
if(lheight==-1 || rheight==-1 ||(abs(lheight-rheight)>1)) return -1;
//return 0; Be sure to return the height. How to calculate the difference if you don't return the height? The difference is greater than 1
return 1+max(lheight,rheight);
}
bool isBalanced(TreeNode* root) {
// int res=height(root);
//if (res==-1)
// {
// return false;
//}
//return true ;
//After code reduction
return getDepth(root) == -1 ? false : true;
}
};
3. Judge subtree vs judge equality
To judge whether a tree t is a subtree of tree s, you can judge whether t is equal to any subtree of tree s. Then it turns into 100 Same Tree.
That is, the method of this problem is to judge whether the child node is equal to t on each child node of s.
The three conditions for judging whether two trees are equal are the relationship between and, namely:
The root node values of the current two trees are equal;
Moreover, the left subtree of s is equal to the left subtree of t;
Moreover, the right subtree of s is equal to the right subtree of t.
The three conditions for judging whether t is a subtree of s are or relations, namely:
The current two trees are equal;
Alternatively, t is the left subtree of s or the subtree of the left subtree;
Alternatively, t is the right subtree of s or the subtree of the right subtree.
**Judge Equality:
class Solution {
public:
bool issame(TreeNode* cur1, TreeNode* cur2)
{
if(cur1==NULL && cur2==NULL) return true;
if(cur1==NULL && cur2!=NULL) return false;
if(cur1!=NULL && cur2==NULL) return false;
bool l=issame(cur1->left,cur2->left);
bool r=issame(cur1->right,cur2->right);
if(cur1->val==cur2->val && l && r)
return true;
return false;
}
bool isSameTree(TreeNode* p, TreeNode* q) {
return issame(p,q);
}
};
Judge subtree:
`class Solution {
public:
bool issame(TreeNode* cur1, TreeNode* cur2)
{
if(cur1==NULL && cur2==NULL) return true;
if(cur1==NULL && cur2!=NULL) return false;
if(cur1!=NULL && cur2==NULL) return false;
bool l=issame(cur1->left,cur2->left);
bool r=issame(cur1->right,cur2->right);
if(cur1->val==cur2->val && l && r)
return true;
return false;
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if(!root && !subRoot) return true; // Both nodes are empty and return the same value
if((root&&!subRoot) || (!root&&subRoot)) return false; // Only one of the two nodes is empty, and the return is different
bool ans= issame(root,subRoot) || isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
return ans;
}
};
`**
4. Construct binary tree
4.1 force buckle 106 Constructing binary tree from middle order and post order traversal sequences
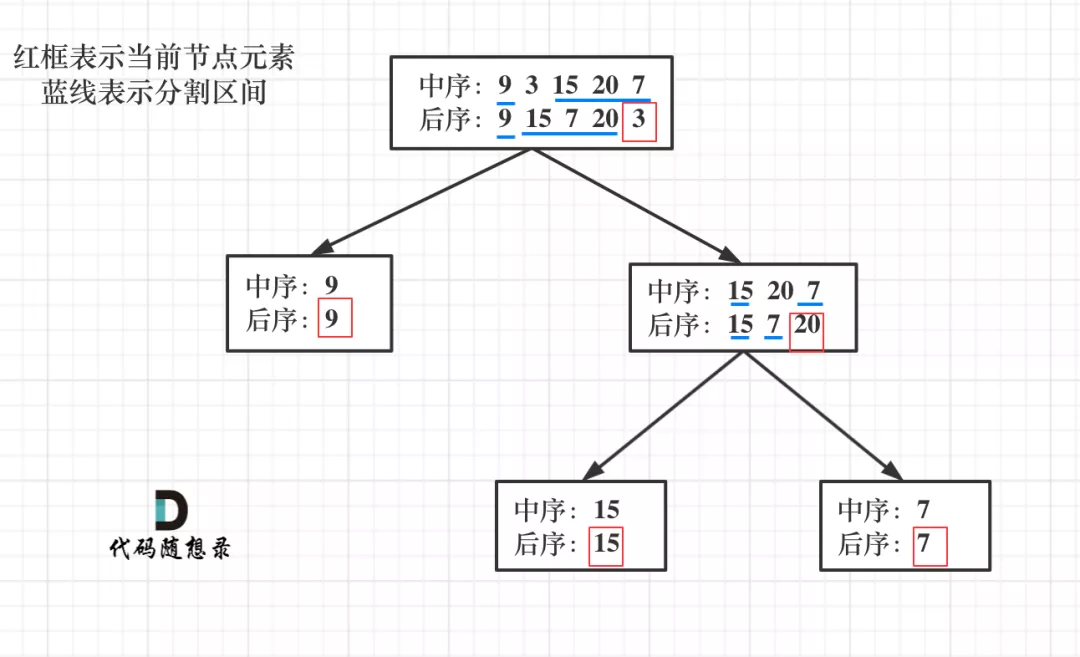
When it comes to cutting layer by layer, we should think of recursion.
Let's take a look at the following steps:
Step 1: if the array size is zero, it indicates that it is an empty node.
Step 2: if it is not empty, take the last element of the subsequent array as the node element.
Step 3: find the position of the last element of the sequential array in the sequential array as the cutting point
Step 4: cut the middle order array into middle order left array and middle order right array (don't reverse the order, you must cut the middle order array first)
Step 5: cut the post order array into the post order left array and post order right array
Step 6: recursively handle the left and right intervals
The cutting point is the last element of the subsequent array, which is used to cut the middle order array, so it is necessary to cut the middle order array first.
The middle order array is relatively easy to cut. Find the position of the cutting point (the last element of the later order array) in the middle order array, and then cut,
The post order array does not have clear cutting elements to cut left and right. Unlike the mid order array, which has clear cutting points, the cutting points can be separated from left and right.
At this time, a very important point is that the size of the middle order array must be the same as that of the later order array (this is inevitable).
If we cut the middle order array into the left middle order array and the right middle order array, then the rear order array can be cut according to the size of the left middle order array and cut into the left rear order array and the right rear order array.
class Solution {
public:
//p is middle order traversal and q is post order traversal
TreeNode* traversal(vector<int>& p, vector<int>& q)
{
//1. If the array size is zero, it is an empty tree
if(p.size()==0 || q.size()==0) return NULL;
//2. The last number of post order traversal is the root node, which can also be used for mid order traversal
int rootval=q[q.size()-1];
TreeNode* root=new TreeNode(rootval);//
//Judge whether it is a leaf node
if (q.size() == 1) return root;
//Non leaf node
int delimiterindex;
for( delimiterindex=0;delimiterindex<p.size();delimiterindex++ )
{
if(p[delimiterindex]==rootval)
break;
}
//Note: vector < int > V2 (V1. Begin(), v1 end())
//Copy the interval element of [v1.begin(),v1.end()) to v2
//v1.end() refers to the next element of the V1 last element
//3. Cut middle order array
vector<int> pl(p.begin(),p.begin()+delimiterindex);
vector<int> pr(p.begin()+delimiterindex+1,p.end());
//4. Cut the post order array (the number of left and right intervals of post order array and middle order array is the same, and the last number is discarded)
//Method 1:
// q.resize( q.size()-1 );
//vector<int> ql(q.begin(),q.begin()+pl.size());
//vector<int> qr(q.begin()+pl.size(),q.end());
//Method 2:
vector<int> ql(q.begin(),q.begin()+pl.size());
vector<int> qr(q.begin()+pl.size(),q.end()-1);
//5. Recursively process the left and right arrays of middle order and post order
root->left=traversal(pl,ql);
root->right=traversal(pr,qr);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
//if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder,postorder);
}
};
4.2 force buckle 105 Constructing binary tree from preorder and inorder traversal sequences
class Solution {
public:
//p is middle order traversal and q is pre order traversal
TreeNode* traversal(vector<int>& p, vector<int>& q)
{
//1. If the array size is zero, it is an empty tree
if(p.size()==0 || q.size()==0) return NULL;
//2. The first number of preorder traversal is the root node, or the preorder traversal can be cut
int rootval=q[0];
TreeNode* root=new TreeNode(rootval);//
//Judge whether it is a leaf node
if (q.size() == 1) return root;
//Non leaf node
int delimiterindex;
for( delimiterindex=0;delimiterindex<p.size();delimiterindex++ )
{
if(p[delimiterindex]==rootval)
break;
}
//Note: vector < int > V2 (V1. Begin(), v1 end())
//Copy the interval element of [v1.begin(),v1.end()) to v2
//v1.end() refers to the next element of the V1 last element
//3. Cut middle order array [0, delimitrindex)
vector<int> pl(p.begin(),p.begin()+delimiterindex);
vector<int> pr(p.begin()+delimiterindex+1,p.end());
//4. Cut the pre order array (the number of left and right intervals of the pre order array and the middle order array is the same)
//Discard the first element
vector<int> ql(q.begin()+1,q.begin()+1+pl.size());
vector<int> qr(q.begin()+1+pl.size(),q.end());
//5. Recursively process the left and right arrays of middle order and post order
root->left=traversal(pl,ql);
root->right=traversal(pr,qr);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return traversal(inorder,preorder);
}
};
5. Path sum
5.1 given a binary tree and a target sum, judge whether there is a path from root node to leaf node in the tree. The sum of all node values on this path is equal to the target sum.
Note: leaf nodes refer to nodes without child nodes.
In this problem, we need to traverse the path from the root node to the leaf node to see if the sum is the target sum
1. Determine the parameters and return type of recursive function
Parameter: the root node of the binary tree and a counter are required. This counter is used to calculate whether the sum of one edge of the binary tree is exactly the target sum. The counter is of type int.
Let's look at the return value. When does a recursive function need a return value? When is the return value not required? Here are three points:
If you need to search the whole binary tree and do not need to deal with the recursive return value, the recursive function will not return the value. (this situation is 113. Path summation ii introduced in the second half of this paper)
If you need to search the whole binary tree and need to process the recursive return value, the recursive function needs to return the value. (we introduce this situation in 236. The nearest common ancestor of binary tree)
If you want to search for one of the qualified paths, recursion must return a value, because if you encounter a qualified path, you must return it in time. (situation of this topic)
In this problem, we need to find a path that meets the conditions, so the recursive function needs to return the value in time. What is the return type?
Insert picture description here
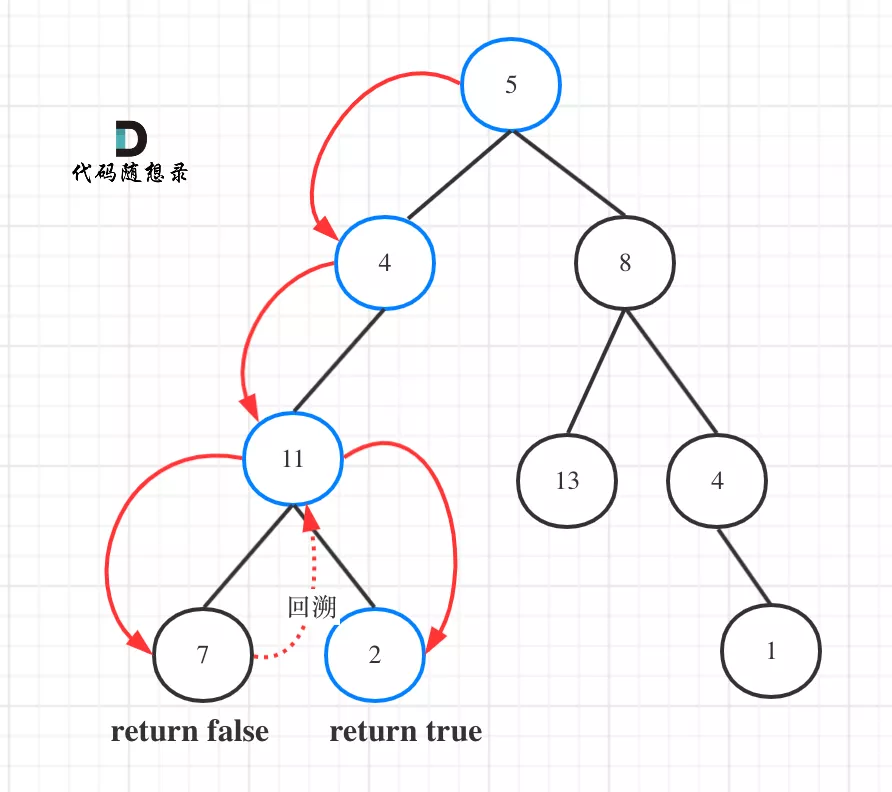
As can be seen from the figure, the traversal route does not traverse the whole tree, so the recursive function needs to return a value, which can be represented by bool type.
2. Determine termination conditions
First, how does the counter count the sum of this path?
Instead of accumulating and then judging whether it is equal to the target sum, the code is more troublesome. You can use decrement to make the counter count initially the target sum, and then subtract the value on the traversal path node each time.
If the last count == 0 and the leaf node is reached at the same time, the target and target are found.
If the leaf node is traversed and the count is not 0, it is not found.
Iteration:
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root==NULL) return false;
//pair structure to store the elements in the stack
//Creation method 1: pair < type, type > P (value1, Value2);
//Creation method 2: pair < type, type > P = make_ pair(value1,value2);
//Pair < tree node *, int > pair < node pointer, path value >
stack<pair<TreeNode*, int>> st;
//Using pair structure to store arrays in the stack
pair<TreeNode*, int> p (root,root->val);
st.push(p);
while(!st.empty())
{
pair<TreeNode*, int> node=st.top();
st.pop();
if(node.first->left==NULL && node.first->right==NULL && node.second==targetSum )
return true;
if(node.first->right)
{
st.push( pair<TreeNode*, int> (node.first->right, node.second+node.first->right->val));
}
if(node.first->left)
{
st.push( pair<TreeNode*, int> (node.first->left, node.second+node.first->left->val));
}
}
return false;
}
};
Recursion:
class Solution {
public:
bool traversal(TreeNode* cur, int t)
{
//Termination condition: leaf node and value is 0
if(!cur->left && !cur->right && t==0)
{
return true;
}
if(!cur->left && !cur->right && t!=0)
return false;
if(cur->left)
{
t-=cur->left->val;
if(traversal(cur->left,t)) return true;
t+=cur->left->val;
}
if(cur->right)
{
t-=cur->right->val;
if(traversal(cur->right,t)) return true;
t+=cur->right->val;
}
//Lite
if (cur->left)
{ // Left (empty nodes do not traverse)
// If the leaf node returns true, it returns true directly
if (traversal(cur->left, count - cur->left->val))
return true; // Notice the logic of backtracking
}
if (cur->right)
{ // Right (empty nodes do not traverse)
// If the leaf node returns true, it returns true directly
if (traversal(cur->right, count - cur->right->val))
return true; // Notice the logic of backtracking
}
//If none of the paths match, false is returned;
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root==NULL) return false;
return traversal(root,targetSum-root->val);
}
};
113. Path sum
Give you the root node of the binary tree root and an integer target and targetSum, and find all the paths from the root node to the leaf node whose total path is equal to the given target sum.
A leaf node is a node that has no child nodes.
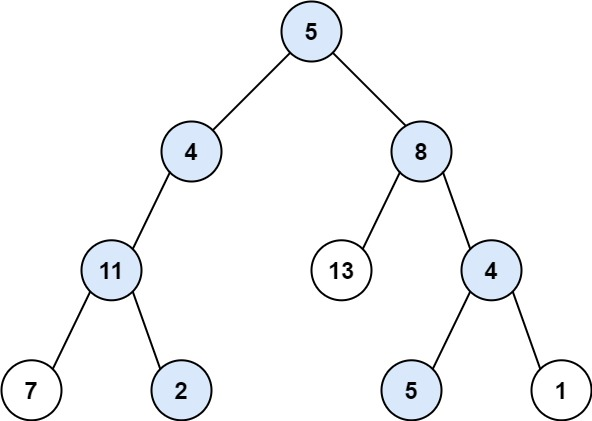
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2], [5,8,4,5]
class Solution {
private:
vector<vector<int>> res;
vector<int> path;//Every path is recorded
//Only qualified ones can be put into res
void traversal(TreeNode* cur, int t)
{
if(!cur->left && !cur->right && t==0)
{
res.push_back(path);
return;
}
if(!cur->left && !cur->right)
return;
if(cur->left)
{
path.push_back(cur->left->val);
t-=cur->left->val;
traversal(cur->left,t);
t+=cur->left->val;
path.pop_back();
}
if(cur->right)
{
path.push_back(cur->right->val);
t-=cur->right->val;
traversal(cur->right,t);
t+=cur->right->val;
path.pop_back();
}
return;
}
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
res.clear();
path.clear();
if(root==NULL)
{
return res;
}
path.push_back(root->val); // Put the root node into the path
traversal(root,targetSum-root->val);
return res;
}
};
6. Search Binary Tree
The binary search tree is an ordered tree:
If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node;
If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node;
Its left and right subtrees are also binary search trees
Question 700: given the root node and a value of a binary search tree (BST). You need to find the node whose node value is equal to the given value in BST. Returns the subtree with this node as the root. NULL if the node does not exist.
class Solution {
public:
/*
TreeNode* traversal(TreeNode* cur, int val)
{
if(cur==NULL) return NULL;
else if(cur->val==val)
return cur;
else if(cur->val>val)
{
return traversal( cur->left,val);
}
return traversal( cur->right,val);
}
TreeNode* searchBST(TreeNode* root, int val) {
return traversal(root,val);
*/
TreeNode* searchBST(TreeNode* root, int val) {
while(root!=NULL)
{
if(root->val>val)
root=root->left;
else if(root->val<val)
root=root->right;
else
return root;
}
return NULL;
}
};
7. Verify search Binary Tree
Because the search binary tree is arranged in order, you can output the array in medium order to judge whether it is orderly
Trap 1
You cannot simply compare that the left node is smaller than the middle node and the right node is larger than the middle node.
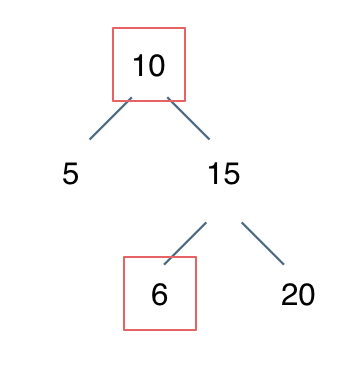
Node 10 is larger than left node 5 and smaller than right node 15, but a 6 appears in the right subtree, which is inconsistent!
In the middle order traversal of binary tree, we talked about the characteristics of traversing binary tree in middle order. In the figure below, when using middle order traversal to traverse binary tree, the access order of nodes is
a1 -> a -> a2 -> b -> c1 -> c -> c2
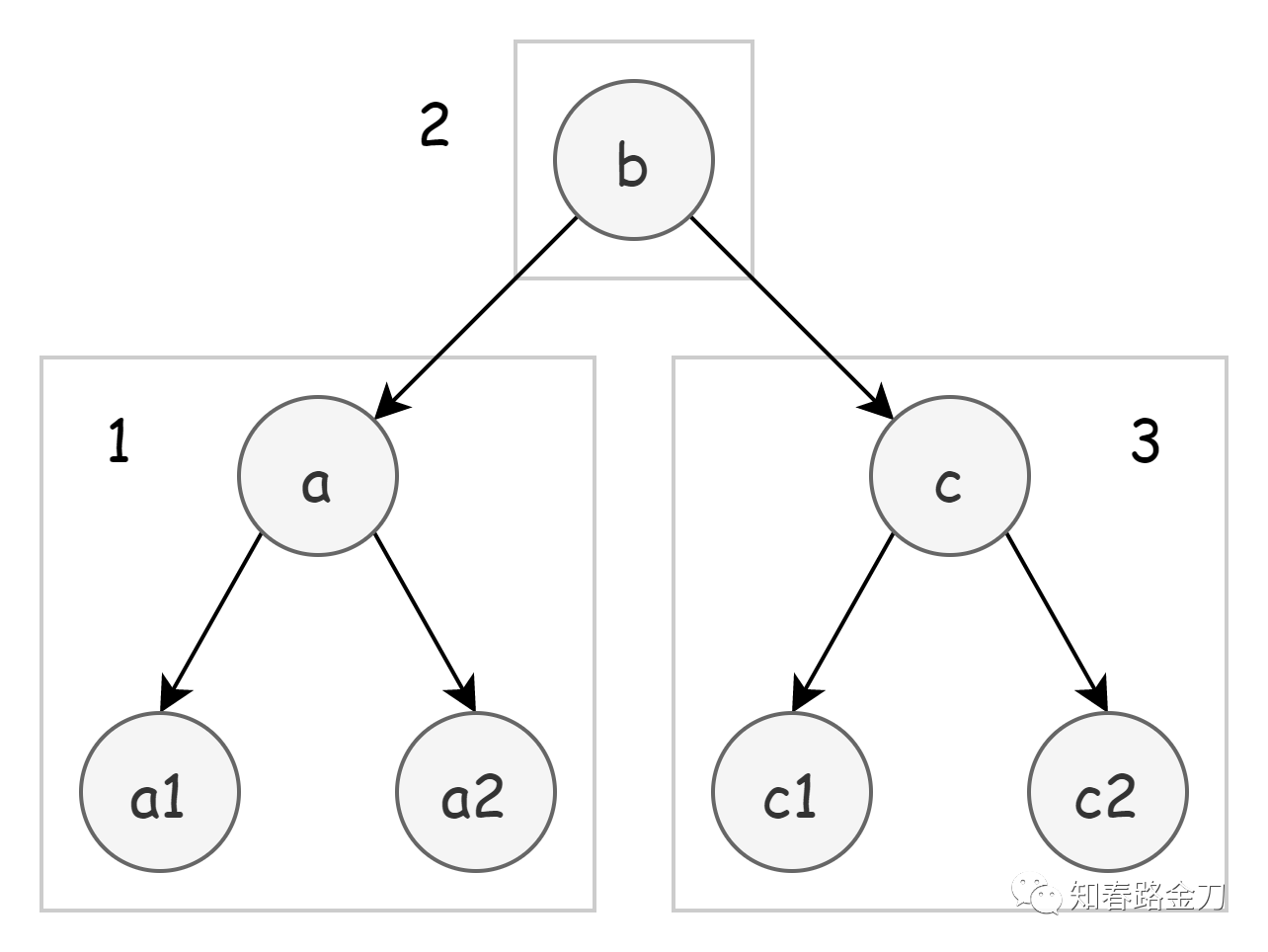
If it is a binary search tree, the access order of nodes should be monotonically increasing, and
a1 < a < a2 < b < c1 < c < c2
We can use this feature to add a last pointer to save the last visited node to judge with the current node
If the current node is larger than the previous node, it means that it meets the definition of binary search tree and continues to make recursive judgment
Otherwise, false is returned directly
class Solution {
public:
TreeNode* pre = NULL; // Used to record the previous node
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root; // Record previous node
bool right = isValidBST(root->right);
return left && right;
}
};
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // Convert binary search tree to ordered array
traversal(root->right);
}
public:
bool isValidBST(TreeNode* root) {
vec.clear(); // It's OK not to add this sentence to leetcode, but it's best to add it
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// Note that it should be less than or equal to. There cannot be the same element in the search tree
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};