1. Trees
Nonlinear data structure
Trees are recursively defined
Each tree is composed of root + multiple subtrees, and the subtree structure is the same
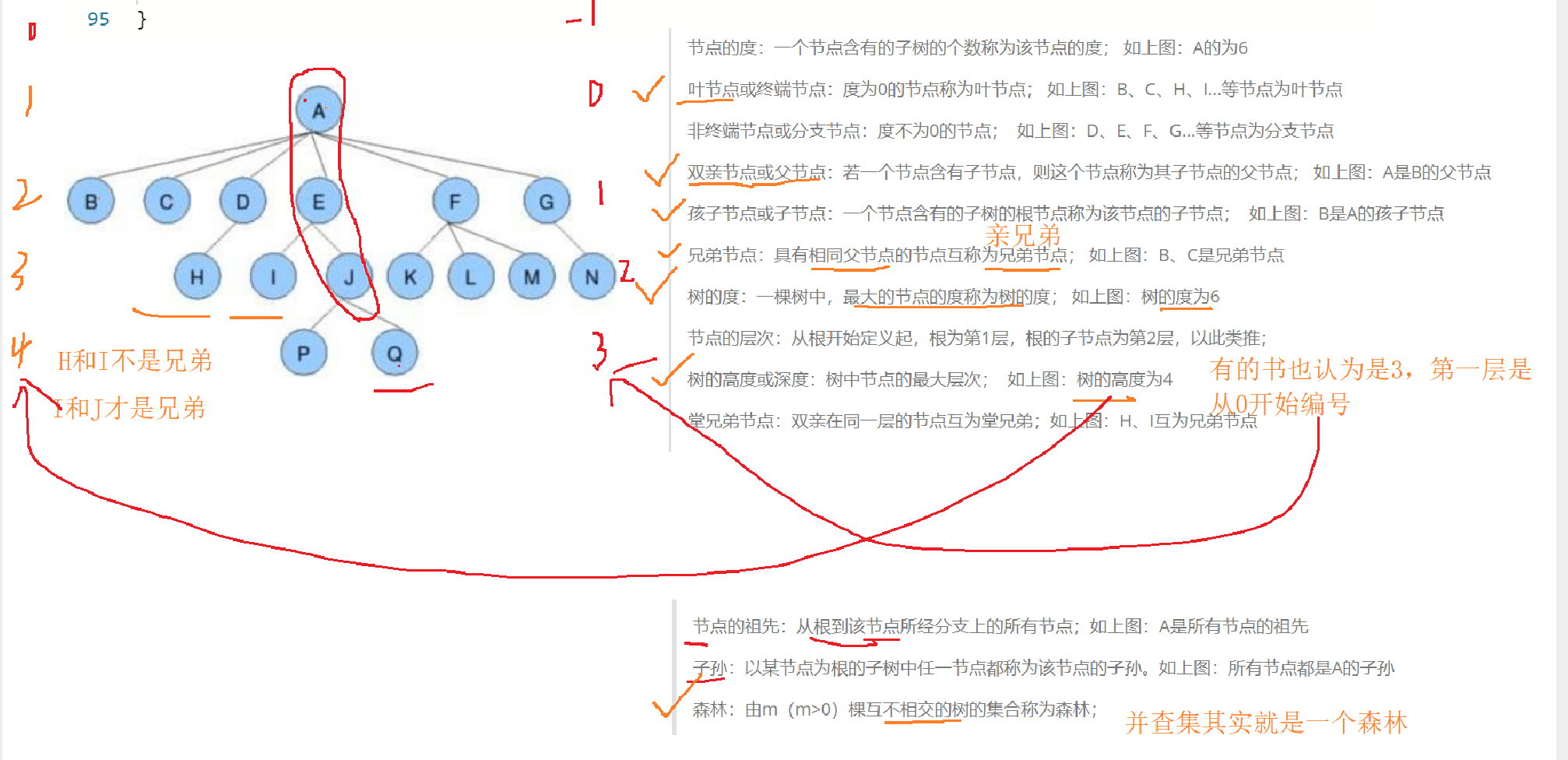
Representation of trees
The tree has no rules on how many children he has
C + + will be easier to write

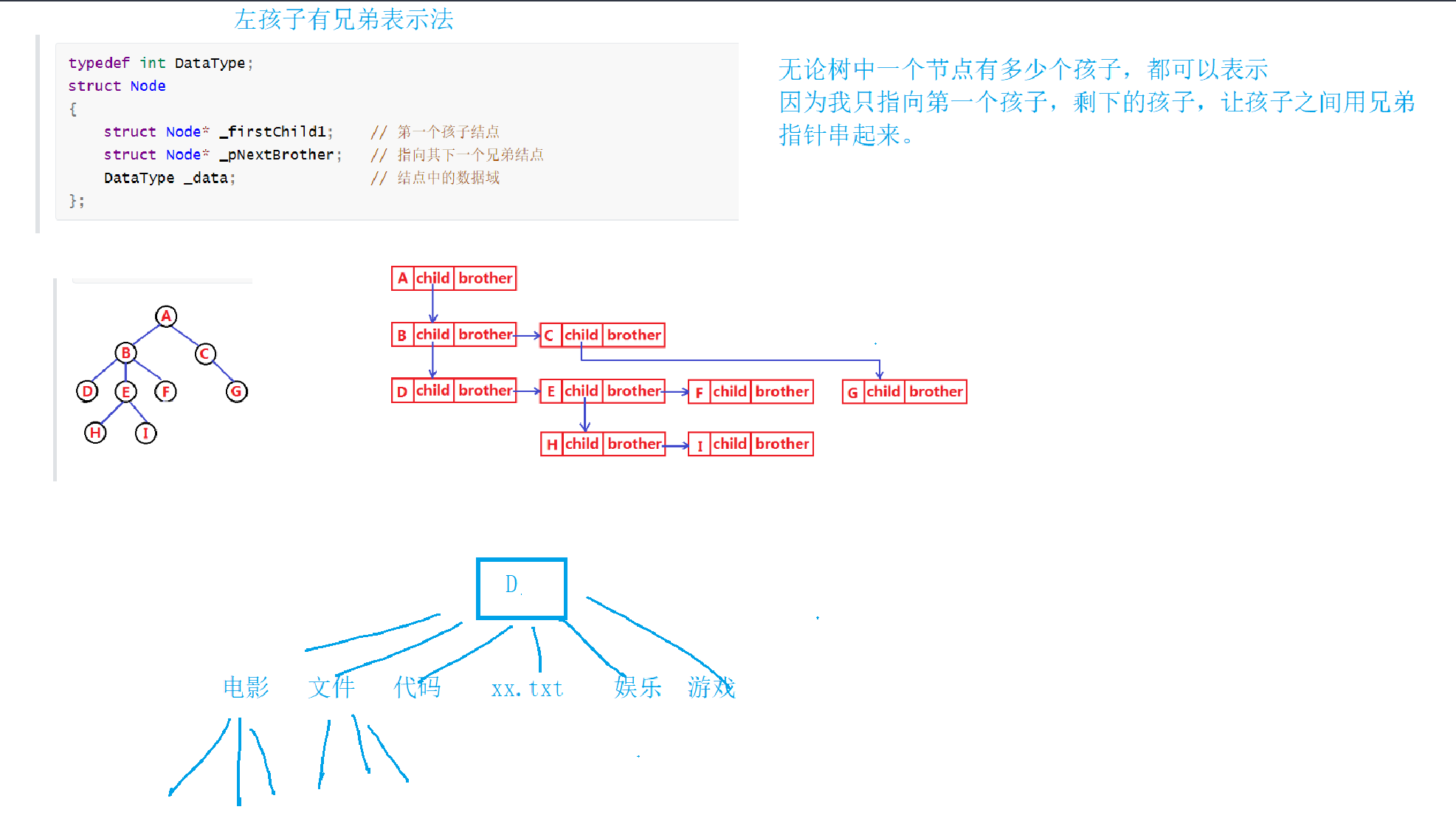
Left child right brother notation
struct Node
{
struct Node* _firstChild1;//first child node
struct Node* _pNextBrother;//Point to its next sibling node
int _data;
}
Parental representation
Each value stores the subscript of the parent
Save it in the array and save the structures one by one
A's father is - 1
B. C's father is 0

2. Binary tree
Degree of binary tree < = 2
Full binary tree & complete binary tree
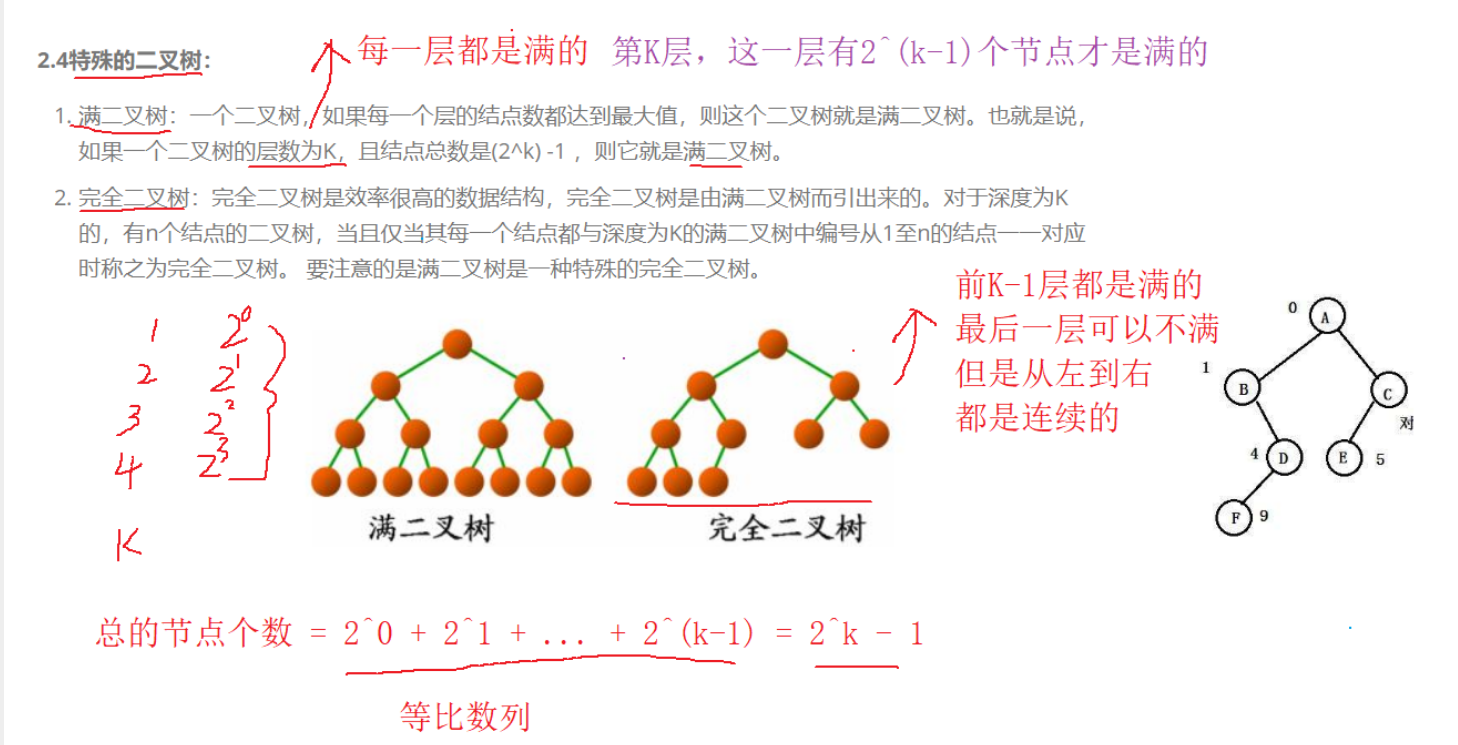
The first k-1 layer of a complete binary tree is full, and the last layer is continuous from left to right
nature

A degree of 0 is one more than a degree of 2
🏷n0 = n2 +1
Binary tree summary point: n0+n1+n2
There is at most one node with moderate 1 in a complete binary tree, that is, a1=0 or a1=0
😆
Storage mode
Sequential storage
Use array storage: applicable to complete binary tree
If it is an incomplete binary tree, there may be a lot of space waste when it is stored in an array
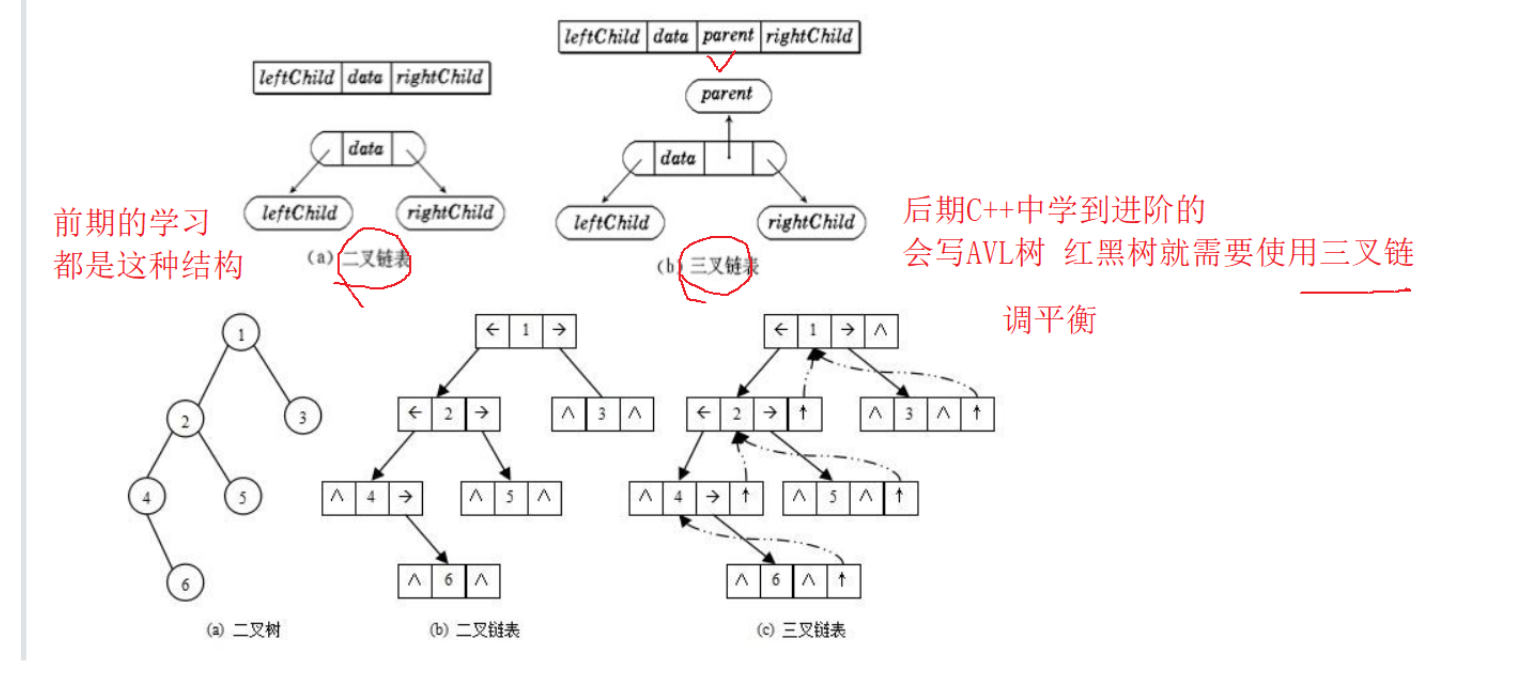
Linked Storage
Binary chain
Trigeminal chain
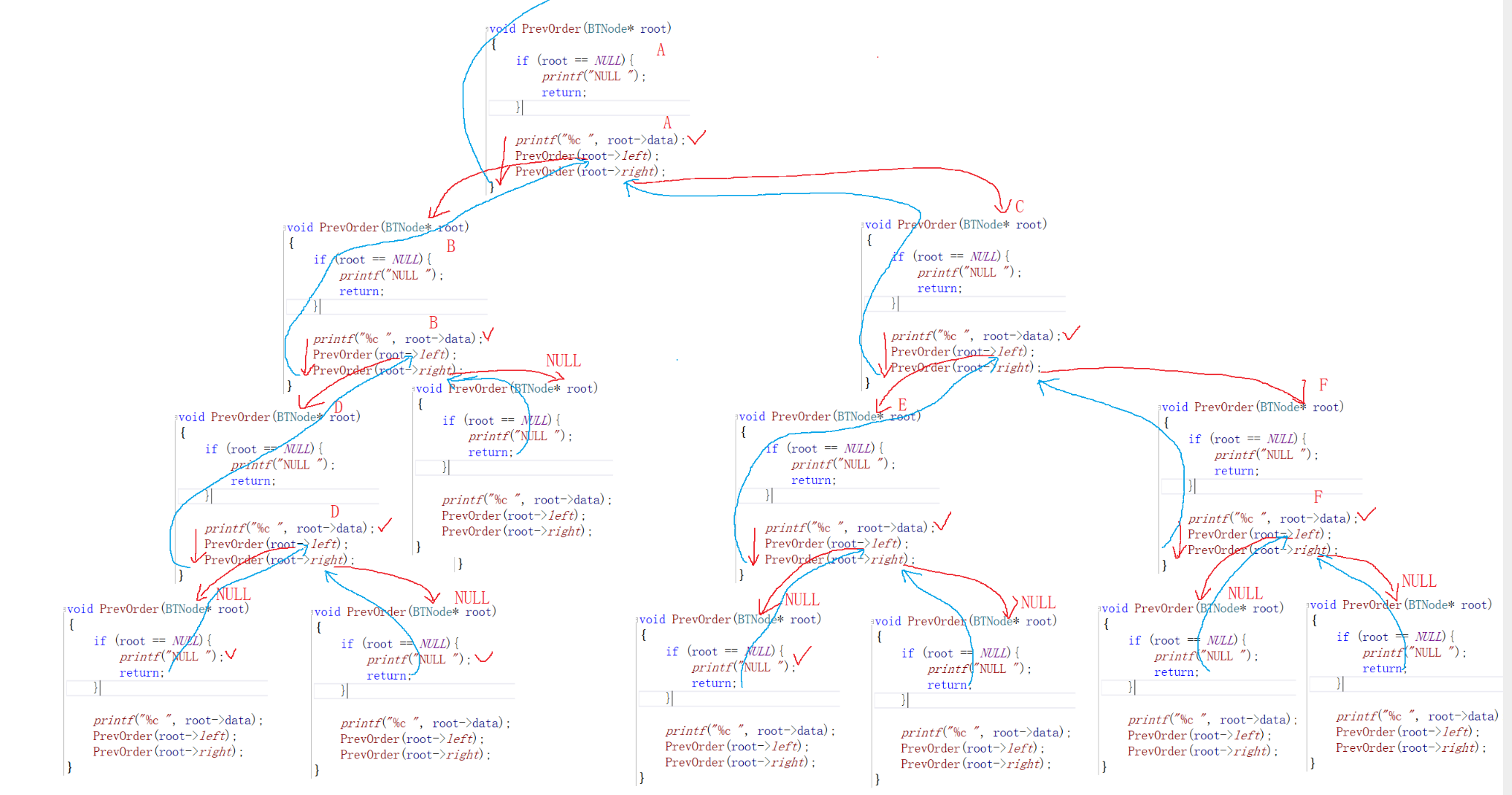
traversal order
- Preorder traversal and root traversal (left and right roots)
- Middle order traversal middle root traversal (left root right)
- Post order traversal (left and right roots)
- The sequence traverses layer by layer
//When the function is called, go back to the place where it was called
The addition, deletion, search and modification of ordinary binary tree is meaningless
If linear tables should be used to store data, binary trees are complicated
And it's not easy to define where to insert and delete
Binary tree application
Huffman tree
Search tree: AVL tree, red black tree
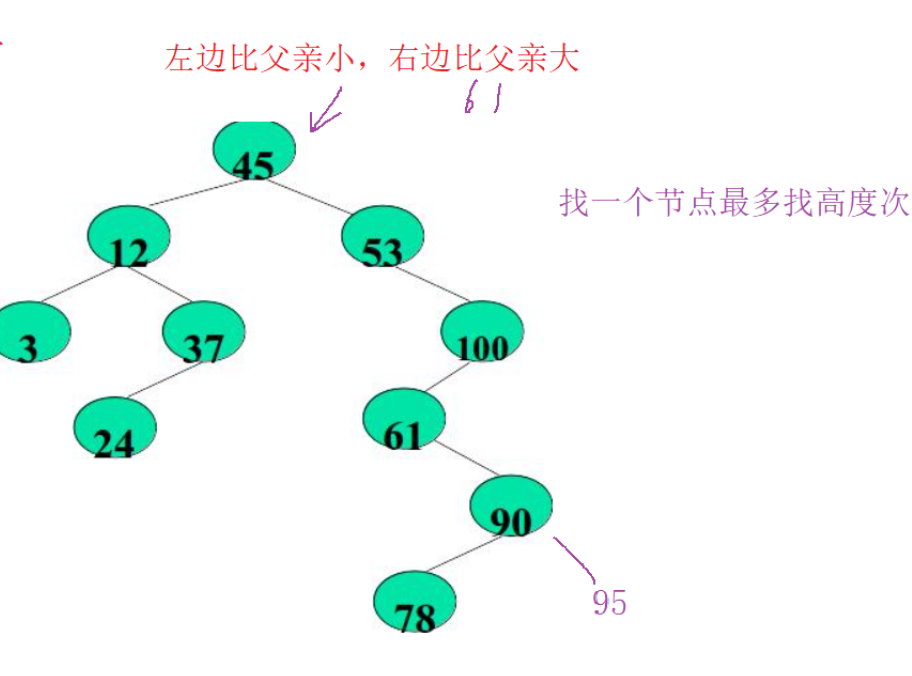
Sorted binary tree
In extreme cases, the efficiency of searching binary tree degenerates to O(N), which is similar to that of linked list and greatly reduced. How to solve it:
AVL tree, red black tree = = > balanced tree
TreeSize
//Idea 1: traverse the counter
void TreeSize(BTNode* root, int* psize)
{
if (root == NULL)
{
return;
}
++(*psize);
TreeSize(root->left, psize);
TreeSize(root->right, psize);
}
int size = 0;
TreeSize(A, &size);
printf("TreeSize::%d\n", size);//6
size = 0;
TreeSize(A, &size);
printf("TreeSize::%d\n", size);//6
The result of using global or static variables

//Divide and conquer algorithm breaks down big problems into small ones
int TreeSize(BTNode* root)
{
//Number of nodes = left + right + myself
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
printf("TreeSize::%d\n", TreeSize(A));//6
printf("TreeSize::%d\n", TreeSize(A));//6
TreeLeafSize
//Number of leaf nodes
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
printf("TreeSize::%d\n", TreeLeafSize(A));//3
TreeKLevelSize
//Number of nodes in layer k
//K-1 layer of left subtree + k-1 layer of right subtree
int TreeKLevelSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (1 == k)
{
return 1;
}
return TreeKLevelSize(root->left, k - 1) +
TreeKLevelSize(root->right, k - 1);
}
BinaryTreeDestroy
It is appropriate to burn the left and right roots later
//Generally, the first level pointer is selected. In order to maintain the consistency of the interface, the user should pay attention to null
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestroy(root->left);
BinaryTreeDestroy(root->right);
free(root);
}
BinaryTreeDestroy(A);
A = NULL;
//Or use references in C + +
//void BinaryTreeDestroy(BTNode*& root)
DFS
The first, middle and last order traversal of binary tree is depth first traversal
Depth first is usually achieved by recursion
BFS
Spread out in circles
The breadth first traversal of binary tree is generally realized by means of queue
Breadth first usually relies on queues
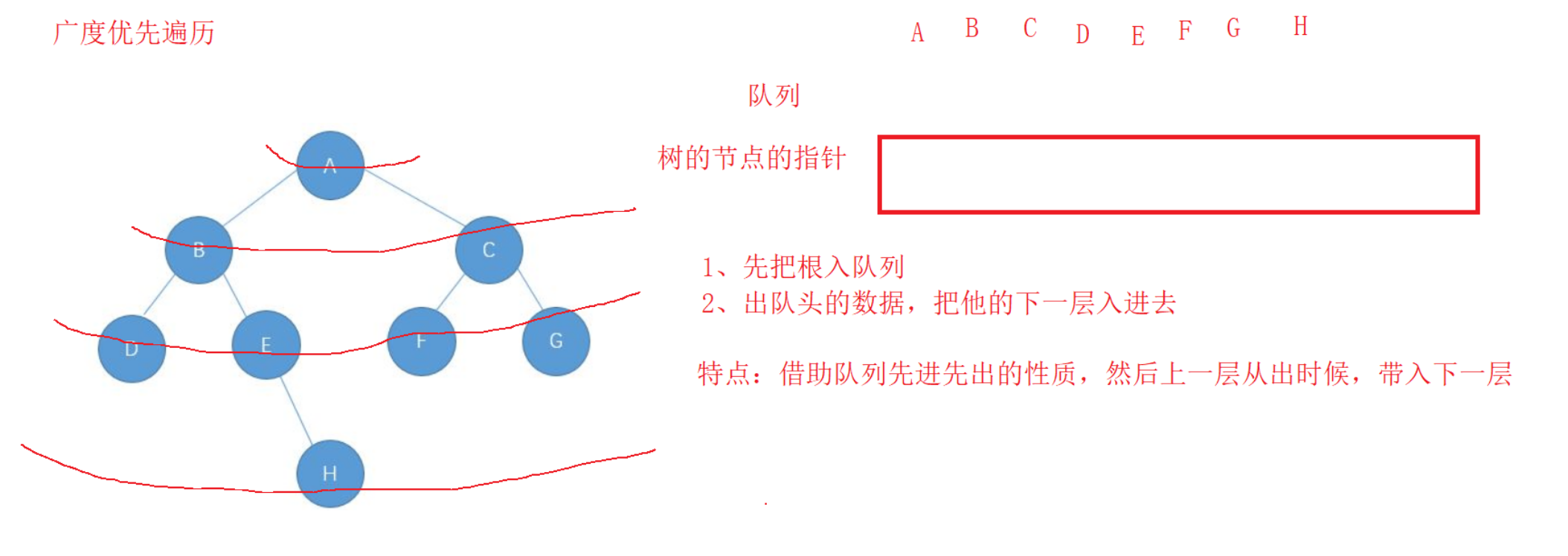
A goes in first, a brings BC in when he comes out, D brings DE in when he comes out, and C brings FG in when he comes out
//breadth-first search
void TreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);//Just pop out the node pointer without destroying the node
printf("%c ", front->data);
//If the left is not empty, bring in the one on the left
if (front->left != NULL)
{
QueuePush(&q, front->left);
}
if (front->right != NULL)
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);
}
//breadth-first search
TreeLevelOrder(A);//A B C D E F
Remember to be in the queue Add the pre declaration of the tree in H, otherwise it will not be compiled
//forward declaration struct BinaryTreeNode;//Define it elsewhere and look for it when you link typedef struct BinaryTreeNode* QDataType;
BinaryTreeComplete
//Judge whether a tree is a complete binary tree
//With the help of sequence traversal, the sequence goes, and the nodes are continuous. When it comes out of the empty space, the whole empty space behind it is a complete binary tree
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//When the first NULL is encountered, jump out and check whether the rest are empty
if (front == NULL)
{
break;
}
//If it is not empty, continue to pass it in
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//Check whether the rest are empty
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
//If it is not completely empty, it is not a complete binary tree
return false;
}
}
QueueDestroy(&q);
//The back is empty
return true;
}
3. Reactor
The physical structure is an array
Complete binary tree
Treat an array as a complete binary tree
Dagendui: father > = child
Little root pile: father < = child
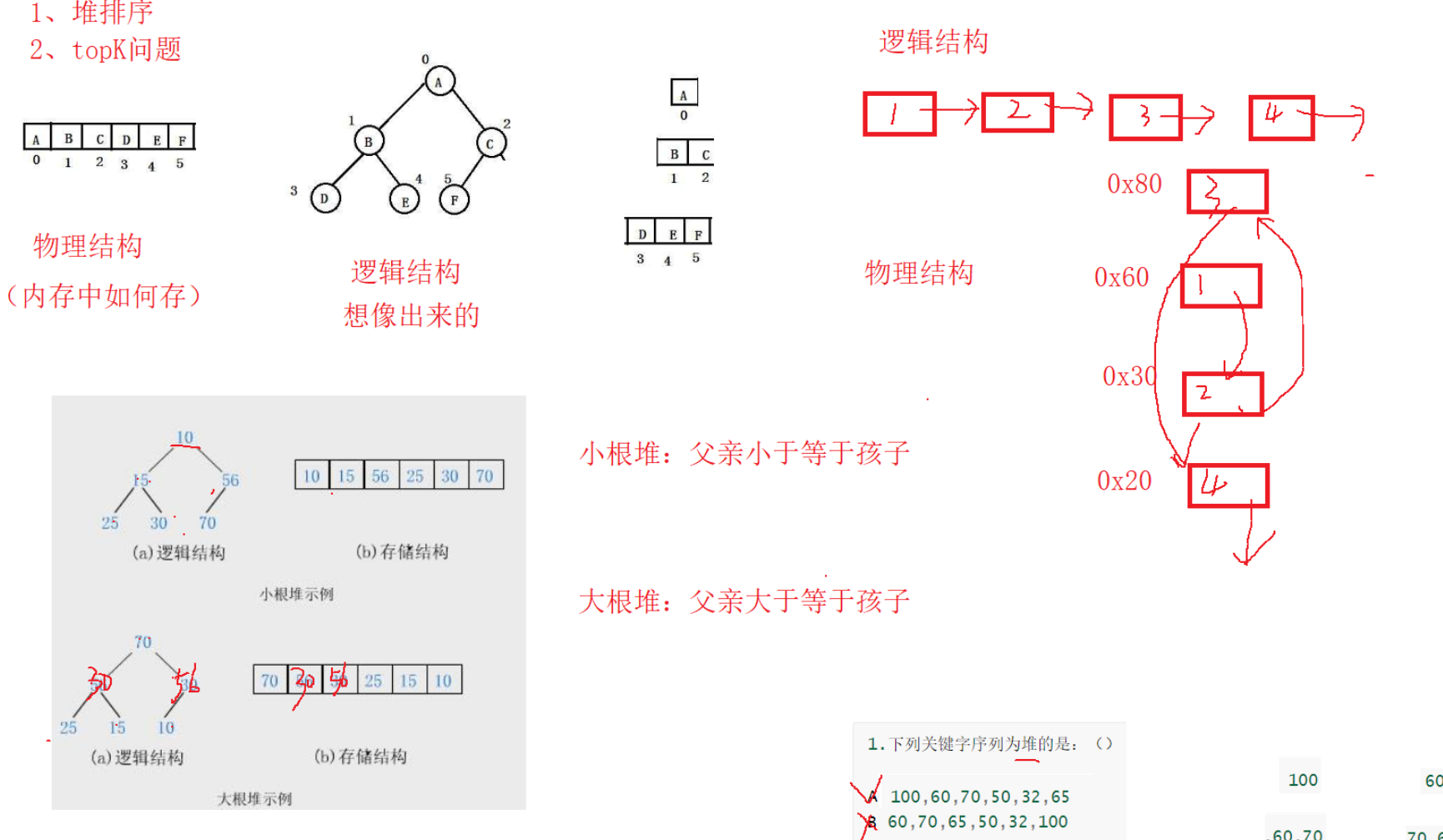
Suppose the father subscript is parent
leftchild = parent*2 + 1;
rightchild= parent*2 + 2;
Can launch==>
parent = (child-1) / 2
(6-1) / 2 => 2
Implementation of heap sorting
If the left and right subtrees happen to be small piles, how to adjust the whole tree into small piles
Downward adjustment algorithm
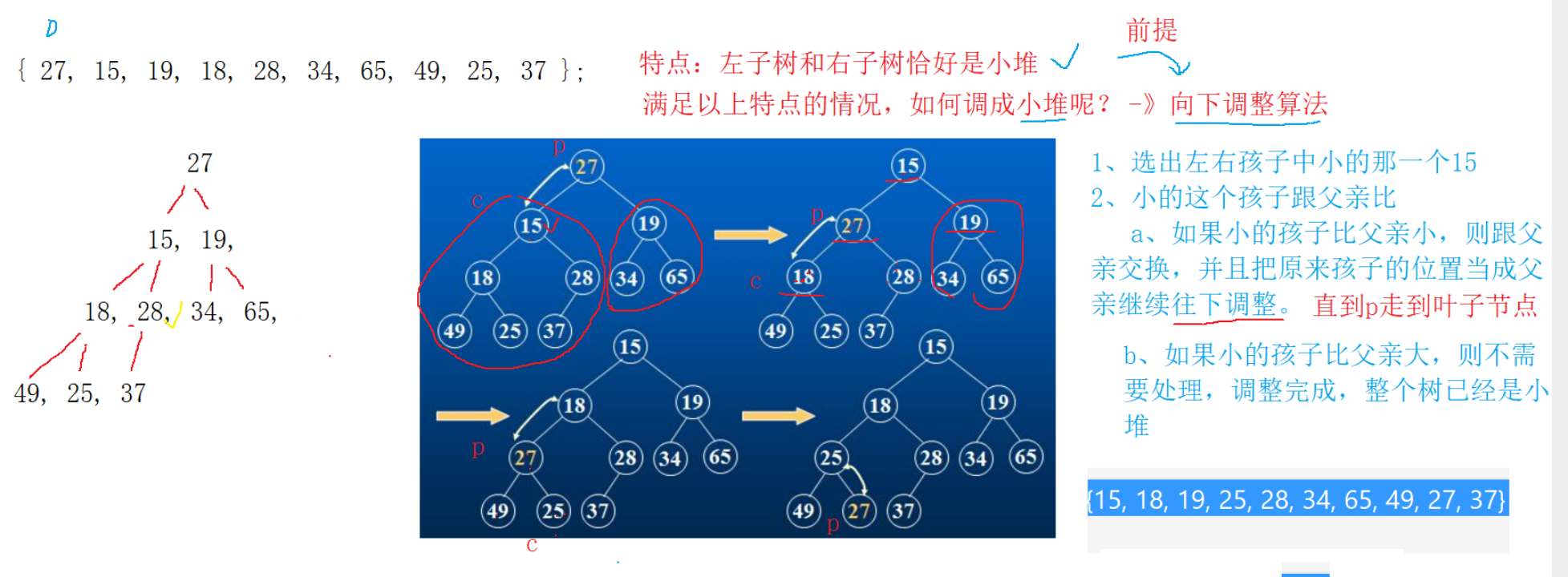
AdjustDown
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
//The parent terminates when it reaches the leaf node, that is, the child coordinate > = n
while (child < n)
{
//Choose the one with the youngest child
if (child + 1 < n && a[child + 1] < a[child])
{
//Child + 1 < n prevents cross-border access to the last right child (assuming there is no last right child)
child++;
}
if (a[child] < a[parent])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
//a[child] >= a[parent]
break;
}
}
}
Heap building algorithm
What if the left and right subtrees are not small piles?
From the penultimate non leaf node (the father of the last node), from back to front, according to the number, take down the adjustment as a subtree in turn

//Heap building algorithm
//n-1 is the subscript of the last node
//Build pile
for (int i = (sz - 1 - 1) / 2; i >= 0; i--)//The father of the last node
//parent = (child-1) / 2
{
AdjustDown(arr, sz, i);
}
//Reactor building time complexity O(N)


HeapSort
Heap sort is better than direct selection sort. O(N^2) is valuable
In ascending heap order, a large heap should be built. If a small heap is built, the parent-child relationship will be changed and the heap needs to be rebuilt. The time complexity of each heap building is O(N), which is too inefficient
Final heap sort time complexity O(N*logN)
HeapSort(int* arr, int sz)
{
for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
{
//The next largest number can be selected only by downward adjustment, and the time complexity is O(logN)
AdjustDown(arr, sz, i);
}
int end = sz - 1;
//Choose the largest number and exchange it to the end
while (end > 0)
{
Swap(&arr[0], &arr[end]);
//Choose the next largest
//The left and right subtrees are a large number, and the next largest number in the original n can be selected from n-1 with only one downward adjustment
AdjustDown(arr, end, 0);
end--;
}
}
int main()
{
int arr[] = { 15,18,28,34,65,19,49,25,37,27 };
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
return 0;
}

Implementation of heap
Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<string.h>
typedef int HPDataType;
struct Heap
{
HPDataType* a;
int size;
int capacity;
};
//Suppose a pile is used
typedef struct Heap HP;
void Swap(int* p1, int* p2);
void AdjustDown(int* a, int n, int parent);
void AdjustUp(int* a, int child);
void HeapInit(HP* php, HPDataType* a, int n);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
int HeapSize(HP* php);
bool HeapEmpty(HP* php);
void HeapPrint(HP* php);
Test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Test()
{
int a[] = { 15,18,28,34,65,19,49,25,37,27 };
int n = sizeof(a) / sizeof(a[0]);
HP hp;
HeapInit(&hp, a, n);
HeapPrint(&hp);
HeapPush(&hp, 8);
HeapPrint(&hp);
HeapPush(&hp, 88);
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
HeapDestroy(&hp);
}
void TopK()
{
//TopK problem
}
int main()
{
Test();
return 0;
}
Init&Destroy
void HeapInit(HP* php, HPDataType* a, int n)
{
assert(php);
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//Copy the array passed in
memcpy(php->a, a, sizeof(HPDataType) * n);
php->size = n;
php->capacity = n;
//Build pile
for (int i = (php->size - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
void HeapPrint(HP* php)
{
for (int i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
int num = 0;
int levelSize = 1;
for (int i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
num++;
if (num == levelSize)
{
printf("\n");
levelSize *= 2;
num = 0;
}
}
printf("\n");
printf("\n");
}
AdjustUp
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
//When while (parent > = 0) Chile = 0, the calculated parent is still 0, and the parent will not be < 0
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
Push
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//It needs to be increased when it is full
if (php->size == php->capacity)
{
HPDataType* tmp = (HPDataType*)realloc(php->a, php->capacity * 2 * sizeof(HPDataType));
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity *= 2;
}
php->a[php->size] = x;
//After inserting data, you need to change the path accordingly and adjust the algorithm upward
php->size++;
AdjustUp(php->a, php->size - 1);
}
Pop
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[php->size - 1], &php->a[0]);
//Delete and change to the last original heap top data
php->size--;
//Adjust downward from 0
AdjustDown(php->a, php->size, 0);
//Similar to the idea of heap sorting, but here is to delete the data in the last position, and heap sorting is ignored
}
Top
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
Size
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
Empty
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
practice
Sword finger Offer 40 Minimum number of k
Top-K problem
Idea 1: sorting
Best sorting time complexity O(N*logN)
Idea 2: build reactor
Build N numbers into a small pile, select one and delete one, and constantly select the first k smallest
Time complexity O(N+logN*k)
Space complexity O(N)
Idea 3: (massive data processing)
Suppose N is very large, 10 billion, and k is 100
If sorting or heap is still used at this time, 40GB space is required, which is not appropriate
First build the first k numbers of the array into a pile
Then the number of N-K is left. Compared with the data on the top of the heap, if it is smaller than the data on the top of the heap, replace the data on the top of the heap, adjust the heap, traverse 10 billion times, and finally the minimum number of K in the heap
Time complexity O(N*logK)
Spatial complexity O(K)
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
//Just build a small pile
HP hp;
HeapInit(&hp, arr, arrSize);
int* retArr = (int*)malloc(sizeof(int)*k);
for(int i=0; i<k; i++)
{
retArr[i] = HeapTop(&hp);
HeapPop(&hp);
}
HeapDestroy(&hp);
*returnSize = k;
return retArr;
}
//s
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
//Handle separately when k=0
if(k == 0)
{
*returnSize = 0;
return NULL;
}
int* retArr = (int*)malloc(sizeof(int)*k);
//First k number
for(int i=0; i<k; i++)
{
retArr[i] = arr[i];
}
for(int j=(k-1-1)/2; j>=0; j--)
{
AdjustDown(retArr,k,j);
}
//If the number of remaining N-k is smaller than that at the top of the heap, replace the data at the top of the heap and put it into the heap
for(int i=k; i<arrSize;++i)
{
if(arr[i] < retArr[0])
{
retArr[0] = arr[i];
//After adjustment
AdjustDown(retArr,k,0);
}
}
*returnSize = k;
return retArr;
}
104. Maximum depth of binary tree
//Recursively call the maximum + 1 of the left subtree and the right subtree
int maxDepth(struct TreeNode* root){
if(root == NULL)
{
return 0;
}
return maxDepth(root->left)>maxDepth(root->right)?maxDepth(root->left)+1:maxDepth(root->right)+1;
}
//The time complexity is too high to run
//Calculate the maximum depth of the left and right, but do not save it. You have to calculate O(N^2) later
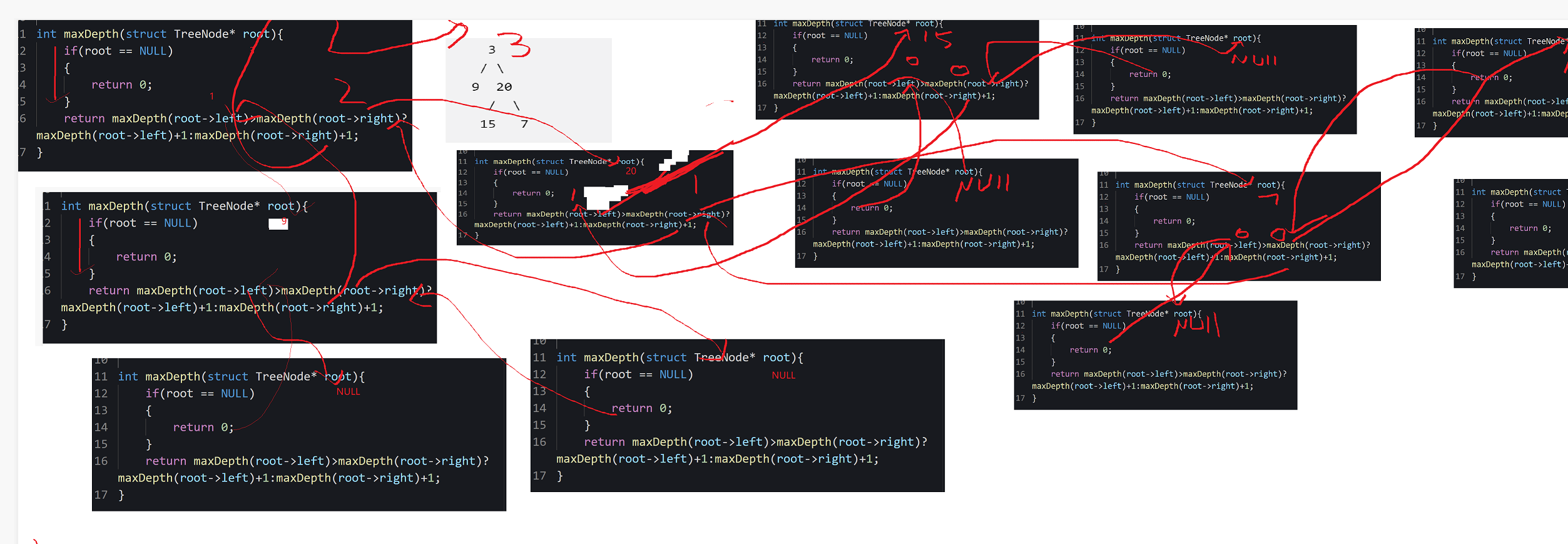
int maxDepth(struct TreeNode* root){
if(root == NULL)
{
return 0;
}
int lMaxDepth = maxDepth(root->left);
int rMaxDepth = maxDepth(root->right);
return lMaxDepth>rMaxDepth?lMaxDepth+1:rMaxDepth+1;
}
//Just save the maximum left and right depth and compare it
//Call fmax function (in C)
//max function in C + +
int maxDepth(struct TreeNode* root){
if(root == NULL)
{
return 0;
}
return fmax(maxDepth(root->left),maxDepth(root->right))+1;
}
//Function call parameters are temporary copies of arguments
965. Single valued binary tree
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
{
return true;
}
//If the left is not empty and the val on the left is not equal to the val of root, it is not a single value
if(root->left != NULL && root->left->val != root->val)
{
return false;
}
//If the right is not empty and the val on the right is not equal to the val of root, it is not a single value
if(root->right != NULL && root->right->val != root->val)
{
return false;
}
//See whether the left is a single value and whether the right is also a single value
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
144. Binary Tree Preorder Traversal
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0:TreeSize(root->left) + TreeSize(root->right) + 1;
}
struct TreeNode* _preorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
if(root==NULL)
return;
//Root left and right
arr[(*pi)++] = root->val;
_preorderTraversal(root->left,arr,pi);
_preorderTraversal(root->right,arr,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
*returnSize = TreeSize(root);
int* arr = (int*)malloc(sizeof(int)*(*returnSize));
int i = 0;
_preorderTraversal(root,arr,&i);//i need to be called by address transmission, otherwise i used in each stack frame development is different
//A sub function can be added_
return arr;
}
100. Same Tree
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL && q==NULL)
return true;
if(p==NULL || q==NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
226. Invert Binary Tree
struct TreeNode* invertTree(struct TreeNode* root){
if(root == NULL)
return NULL;
//Starting from the root node, the tree is traversed recursively, and the leaf node is flipped first
struct TreeNode* left = invertTree(root->left);
struct TreeNode* right = invertTree(root->right);
root->left = right;
root->right = left;
return root;
}
101. Symmetric Tree
Idea 1: recursive traversal
bool _isSymmetric(struct TreeNode* left,struct TreeNode* right)
{
if(left == NULL && right == NULL)
return true;
if(left == NULL || right == NULL)
return false;
if(left->val != right->val)
return false;
return _isSymmetric(left->right, right->left)
&& _isSymmetric(left->left, right->right);
}
bool isSymmetric(struct TreeNode* root){
if(root == NULL)
return true;
bool ret = _isSymmetric(root->left,root->right);
return ret;
}
Idea 2: flip first and then judge whether it is equal
bool isSymmetric(struct TreeNode* root){
if(root == NULL)
return true;
//Just flip one side
root->right = invertTree(root->right);
bool ret = isSameTree(root->left, root->right);
return ret;
}
572. Subtree of Another Tree
T is a subtree of S, that is, a subtree of T and S is equal
Just compare T with all subtrees of S
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL)
return false;
//Traverse each node of the tree, and each node makes the root of the subtree to compare whether it is equal to the subRoot
//Preorder traversal
//There are roots here every time
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
}
110. Balanced Binary Tree
bool isBalanced(struct TreeNode* root){
if(root == NULL)
return true;
//Preorder traversal
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
return abs(leftDepth-rightDepth) < 2
&& isBalanced(root->left)
&& isBalanced(root->right);
}
Time complexity analysis O(N^2)
Suppose it is a full binary tree(Worst case scenario)
isBalanced Recursion N second(In fact, it is depth first)
Every recursion:N N/2 N/2 N/4 N/4 ...
requirement:Optimized to O(N)
Because it is recursive from top to bottom, for the same node, the function maxDepth It will be called repeatedly, resulting in high time complexity.
bool _isBalanced(struct TreeNode* root, int* ph)
{
if(root == NULL)
{
*ph = 0;
return true;
}
//Postorder traversal first determines the left and then the right
//Left imbalance
int leftHeight = 0;
if(_isBalanced(root->left,&leftHeight) == false)
return false;
//Right side imbalance
int rightHeight = 0;
if(_isBalanced(root->right,&rightHeight) == false)
return false;
//Balance left and right, bring the height back to the next level
*ph = fmax(leftHeight,rightHeight) + 1;
return fabs(leftHeight-rightHeight) < 2;
}
bool isBalanced(struct TreeNode* root){
int height = 0;
return _isBalanced(root, &height);
}
Traversal of binary tree in retest of Tsinghua University
Make a program to read in a string of preorder traversal strings entered by the user, and establish a binary tree (stored in the form of pointer) according to this string. For example, the following pre order traversal string: ABC##DE#G##F#### where "#" represents a space, and the space character represents an empty tree. After the binary tree is established, the binary tree is traversed in middle order and the traversal result is output.
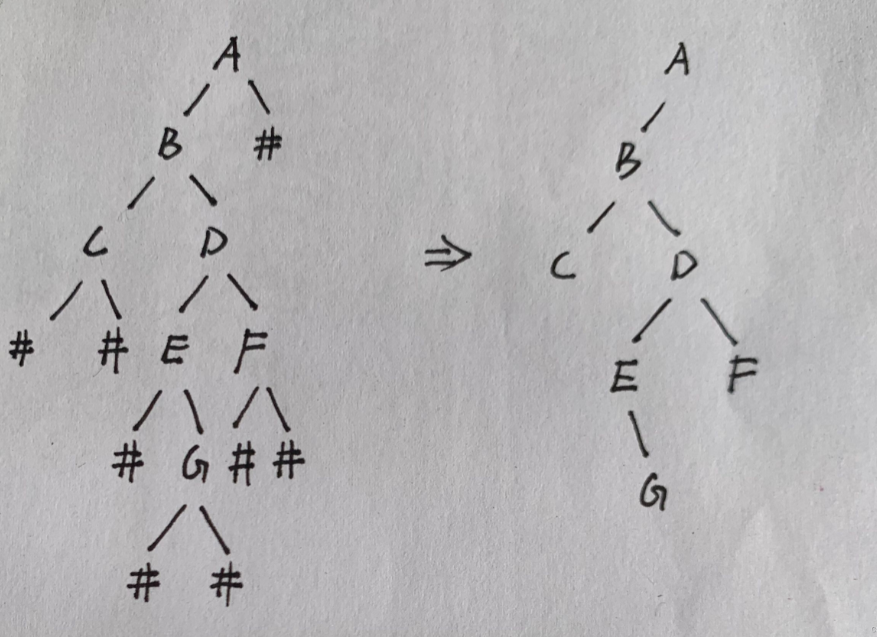
#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode
{
char val;
struct TreeNode* left;
struct TreeNode* right;
}TNode;
TNode* CreateTree(char* a, int* pi)
{
if (a[*pi] == '#'/ / the empty tree does not need recursive construction, but needs i++
{
(*pi)++;
return NULL;
}
//If it is not an empty tree, you need to recursively build the tree
TNode* root = (TNode*)malloc(sizeof(TNode));
if (root == NULL)
{
printf("malloc fail\n");
exit(-1);
}
else
{
root->val = a[*pi];//Takes the value in the current array as the root node value
(*pi)++;
root->left = CreateTree(a, pi);//Recursive construction of left subtree
root->right = CreateTree(a, pi);//Recursive construction of right subtree
return root;
}
}
void InOrder(TNode* root)//Medium order recursive traversal
{
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main()
{
char arr[30] = { 0 };
gets(arr);
int i = 0;
TNode* root = CreateTree(arr, &i);
InOrder(root);
return 0;
}