Binary tree is a special tree data structure. This time, let's learn how to create a binary tree recursively and how to recursively traverse the binary tree. At the same time, the last preorder traversal is an example of non recursive traversal of the binary tree.

To write code, you should know well that the structure of binary tree is more complex than the previous linked list, queue and stack. Therefore, draw more pictures when there is no bottom.

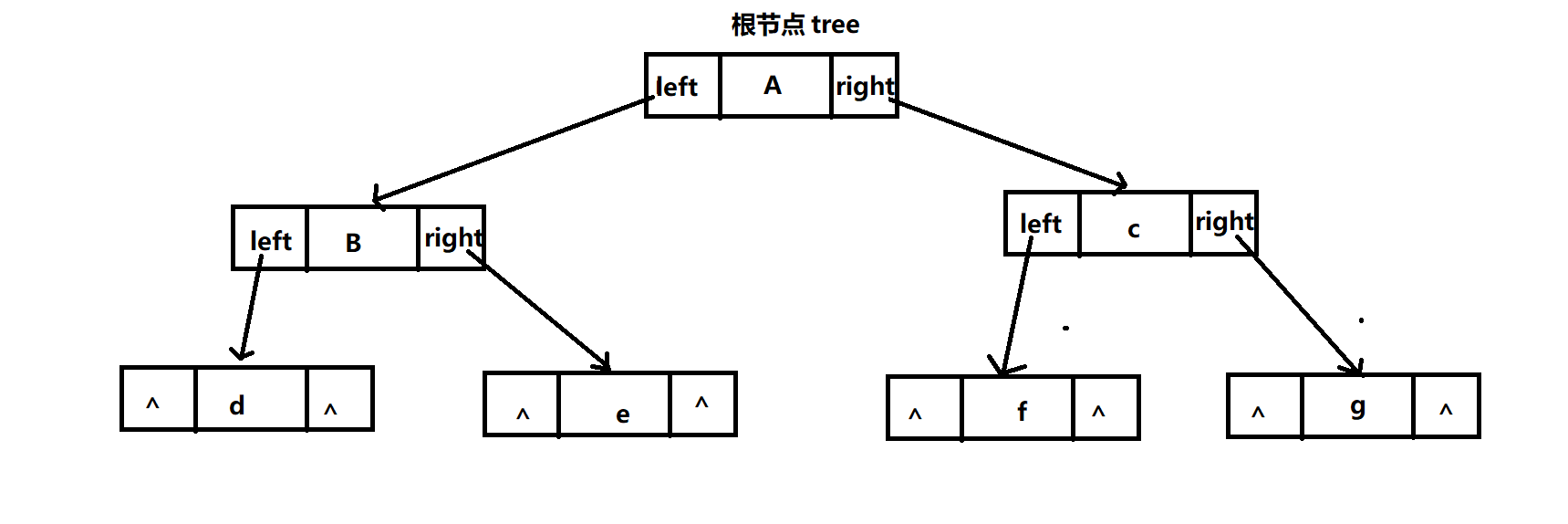
It can be seen from the above figure that the basic structure of the binary tree is a data field and two pointer fields, ^ represents null, so the node constructor of the binary tree is as follows:

//Internal class that holds left and right pointers and data fields
function TreeNode(data){
	this.data=data;
	this.left=null;
	this.right=null;
}

1, Create binary tree recursively

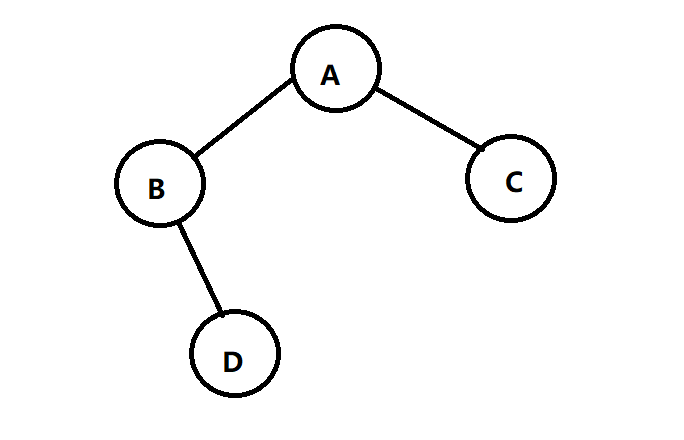
For the above binary tree, if you create it recursively, you can create it node by node, but it is more troublesome, because you have to spend time and energy to determine where the new node needs to be inserted. If you insert it in a way that the left subtree is smaller than the right subtree, it may be simpler, This binary tree is the "binary sort tree" that will be mentioned later. This time, we create an ordinary binary tree, so we construct the binary tree according to the preorder traversal results of the binary tree.

The pre order traversal result of the binary tree in the figure above is: AB#D##C ##, # represents an empty node.

If we know the preorder traversal result of A binary tree, how to construct the binary tree? It's very simple, in A recursive way: according to the string AB#D##C ##, create node A first, and then recursively create left node B of node A, and then recursively get an "#" that is, an empty node. The stewardess point directly returns to node B, so the left of B is null, recursively get the right node of B, and then recurse the left and right subtrees of D in turn, which are null, so they return layer by layer, Know to return to the root node, and then access the right subtree of the root node, so as to complete the construction of A binary tree.

Code demonstration:

BinaryTree.prototype.createTree=function(node){
	let index=wm.get(this)[this.index]++; //The index private variable holds the index to the string
	const data=this.treeStr.split('')[index];
	if(index<this.treeStr.split('').length){
		if (data === '#') {
			node = null;
		} else {
			node = new TreeNode(data);
			node.left = this.createTree(node.left);
			node.right = this.createTree(node.right);
		}
	}
	return node;
}

II. Return binary tree depth

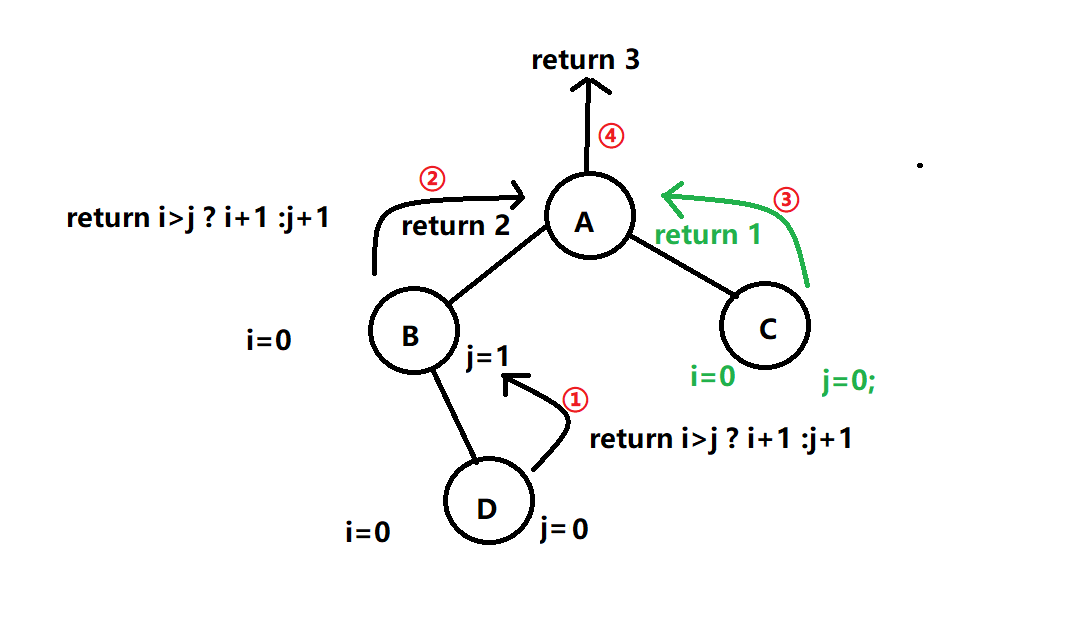
The algorithm for returning the depth is also implemented recursively. First, the left subtree of the tree is recursive. When the left subtree is empty, judge whether there is a right subtree, and recurse if there is. Otherwise, return 0, detect the left subtree through the i variable, j detect the right subtree, and return max(i,j)+1

Code implementation:

/**
 * Returns the depth of the binary tree
 * */
BinaryTree.prototype.treeDepth=function(tree){
	let i,j;
	if(!tree){
		return 0;
	}
	
	if(tree.left){
		i=this.treeDepth(tree.left);
	}else{
		i=0;
	}

	if(tree.right){
		j=this.treeDepth(tree.right);
	}else{
		j=0;
	}

	return i>j ? i+1 : j+1;
}

3, Non recursive preorder traversal

For non recursive traversal, an array stack is used to store node references. For example, the preorder traversal is about the root, so first put node a on the stack, then output node A's data, and then continuously traverse the left subtree. When traversing a node, the node is put on the stack and output until the left subtree is empty. At this time, the variable traversing the node must be null, so it is out of the stack, That is, go back to the previous node and traverse the right subtree of the node. Whether it is empty or not, if it is empty, it will be out of the stack again to the penultimate node. The period is always a cycle control. When all elements are out of the stack or the tree is empty, the cycle ends.

Code demonstration:

/**
 * Non recursive preorder lookup node
 * */
BinaryTree.prototype.preTraversalByStack=function(tree){
	let stack=new Array(); //Initialize a stack array
	while(stack.length>0 || tree){
		
		while(tree){  //When the left subtree is not empty, it is always put on the stack and output
			console.log(tree.data);
			stack.unshift(tree);
			tree=tree.left;
		}

		/**
		 * After the traversal of the left subtree is completed, go out of the stack to the previous reference to find out whether there is a right subtree
		 * */
		if(stack.length>0){
			tree=stack.shift();
			tree=tree.right;
		}
	}
}

Recursive traversal algorithm is simple and will not be repeated.

Complete source code:

'use strict'
//Binary tree
const BinaryTree=function(){
	const wm=new WeakMap();

	//Binary tree constructor
	function BinaryTree(treeStr=""){
		this.treeStr=treeStr;

		this.index=Symbol('private');
		const privateMembers=wm.get(this) || {};
		privateMembers[this.index]=0;
		wm.set(this,privateMembers);

		const node=null;
		this.tree=this.createTree(node);
	}

	//Internal class that holds left and right pointers and data fields
	function TreeNode(data){
		this.data=data;
		this.left=null;
		this.right=null;
	}

	/**
	 * Create tree recursively
	 * Is # considered null for
	 * */
	BinaryTree.prototype.createTree=function(node){
		let index=wm.get(this)[this.index]++;
		const data=this.treeStr.split('')[index];
		if(index<this.treeStr.split('').length){
			if (data === '#') {
				node = null;
			} else {
				node = new TreeNode(data);
				node.left = this.createTree(node.left);
				node.right = this.createTree(node.right);
			}
		}
		return node;
	}

	/**
	 * Returns the depth of the binary tree
	 * */
	BinaryTree.prototype.treeDepth=function(tree){
		let i,j;
		if(!tree){
			return 0;
		}
		
		if(tree.left){
			i=this.treeDepth(tree.left);
		}else{
			i=0;
		}

		if(tree.right){
			j=this.treeDepth(tree.right);
		}else{
			j=0;
		}

		return i>j ? i+1 : j+1;
	}

	/**
	 * Preorder traversal of binary tree
	 * */
	BinaryTree.prototype.preTraversal=function(tree){
		if(tree){
			console.log(tree.data);
			tree.left=this.preTraversal(tree.left);
			tree.right=this.preTraversal(tree.right);
		}
		return tree;
	}

	/**
	 * Medium order traversal
	 * */
	BinaryTree.prototype.midTraversal=function(tree){
		if (tree) {
			tree.left =this.midTraversal(tree.left);
			console.log(tree.data);
			tree.right=this.midTraversal(tree.right);
		}
		return tree;
	}

	/**
	 * Postorder traversal
	 * */
	BinaryTree.prototype.postTraversal=function(tree){
		if (tree) {
			tree.left = this.postTraversal(tree.left);
			tree.right = this.postTraversal(tree.right);
			console.log(tree.data);
		}
		return tree;
	}

	/**
	 * Non recursive preorder lookup node
	 * */
	BinaryTree.prototype.preTraversalByStack=function(tree){
		let stack=new Array(); //Initialize a stack array
		while(stack.length>0 || tree){
			
			while(tree){  //When the left subtree is not empty, it is always put on the stack and output
				console.log(tree.data);
				stack.unshift(tree);
				tree=tree.left;
			}

			/**
			 * After the traversal of the left subtree is completed, go out of the stack to the previous reference to find out whether there is a right subtree
			 * */
			if(stack.length>0){
				tree=stack.shift();
				tree=tree.right;
			}
		}
	}

	return BinaryTree;
}();

const tree=new BinaryTree('ABDH#K###E##CFI###G#J##');
console.log(tree);
tree.postTraversal(tree.tree);
console.log(tree.treeDepth(tree.tree));
tree.preTraversalByStack(tree.tree);