preface

In the process of computer programming, we will use many different kinds of data types, such as number, queue, linked list, etc. each different data type has different data structures. When we contact more data structures, we should have a certain foundation. Let's know the binary tree today.

1, What is a binary tree?

Before we learn about binary trees, let's find out what a tree is.

Definition: a tree is a finite set with n nodes.

• When n=0, there is and only one node, which is called the root node
• When n > 0, the other nodes are divided into m mutually exclusive finite sets T1, T2, T3, and each set is called a subtree

In short, a node has two child nodes, a left node and a right node, and the child nodes have corresponding byte points, so they correspond.

Binary tree is a special form of tree. The characteristic of binary tree is that each node has at most two children (i.e. nodes with no existence degree greater than 2), which are called left children and right children respectively. The subtree of binary tree can be divided into left and right, and the order of subtree can not be reversed.

Approximate graphical model.

2, Binary tree code implementation

In the design of binary tree code implementation, we use the idea of recursion when designing nodes.

public class Node{

        //Each node has three attributes: node value, left child node and right child node
        private Node left;
        private Node right;
        private int value;

        //Nonparametric construction method
        public Node(){}
        //Initialize the node value through the construction method
        public Node(int value){
            this(null,null,value);
        }
        public Node(Node left,Node right,int value){
            this.left=left;
            this.right=right;
            this.value=value;
        }

        //Get and set the left child node
        public Node getLeft(){
            return left;
        }
        public void setLeft(Node left){
            this.left=left;
        }
        //Get and set the right child node
        public Node getRight(){
            return right;
        }
        public void setRight(Node right){
            this.right=right;
        }
        //Get and set node value
        public int getValue() {
            return value;
        }
        public void setValue(int value) {
            this.value = value;
        }
    }

3, Basic properties of trees

• Node: contains data items and branches to other nodes
• Degree of node: the subtree owned by the node. For example, in the above figure, the degree of B is 1, the degree of C is 2, and the degree of D is 3
• Leaf node & terminal node: that is, the node with degree 0. For ex amp le, in the above figure, F, G, H, I and J are leaf nodes
• Branch node & non terminal node: other nodes except leaf nodes
• Child node: if node x has A subtree, the root node of the subtree is the child of node x. For example, in the above figure, A has two children, B and C
• Parent node: if node x has children, it is the parent node of the children
• Root node: a node without a parent node is called a root node
• Sibling node: children of the same parent node are called brothers to each other. For example, in the above figure, D, e and F are brothers
• Ancestor node: all nodes from the root node to the branch experienced by the node. For example, in the above figure, the ancestor nodes of G are a, B and D
• Descendant node: the children of a node and the children of these children are the descendants of the node. For example, in the above figure, the descendants D and G of node B
• The level of the node: the number of branches on the path from the root to the node The root node is in layer 1 and its children are in layer 2. The hierarchy of any node in the tree is the hierarchy of its parent node plus 1. The level of a node is also called the depth of the node
• Height of tree: the height of leaf node is 1, and the height of non leaf node is equal to the maximum height of its child node plus 1. The height of the tree is 4
• Degree of tree: the maximum degree of nodes in the tree. For example, the height of the tree in the above figure is 3

4, Special binary tree

1. Oblique tree

Full binary tree: a full binary tree with depth K is a binary tree with 2^k-1 nodes. In the full binary tree, the number of nodes in each layer reaches the maximum. Except that the node degree of the lowest layer is 0, the node degree of other layers is 2. As shown in the figure, a full binary tree with a height of 4 is given.

2. Full binary tree

Full binary tree: a full binary tree with depth K is a binary tree with 2^k-1 nodes. In the full binary tree, the number of nodes in each layer reaches the maximum. Except that the node degree of the lowest layer is 0, the node degree of other layers is 2. As shown in the figure, a full binary tree with a height of 4 is given.

3. Complete binary tree

If a binary tree with n nodes and a depth of K corresponds to the nodes numbered 1~n in the full binary tree with a height of K, it is called a complete binary tree. Its characteristic is that the nodes of all layers from the first layer to k-1 layer are full, only the lowest k layer is full, or several nodes are missing continuously from right to left.

5, Properties of binary tree

1. There are at most 2^(i-1) nodes on the i-th layer of non empty binary tree
2. A binary tree with depth K has at most 2^k-1 nodes
3. For any binary tree T, if the number of terminal nodes is n0 and the number of nodes with degree 2 is n2, then n0 = n2+1

6, Traversal of binary tree

The most commonly used traversal methods of binary trees are pre order, middle order and post order.

1. Preorder traversal

First root node - > left subtree - > right subtree;

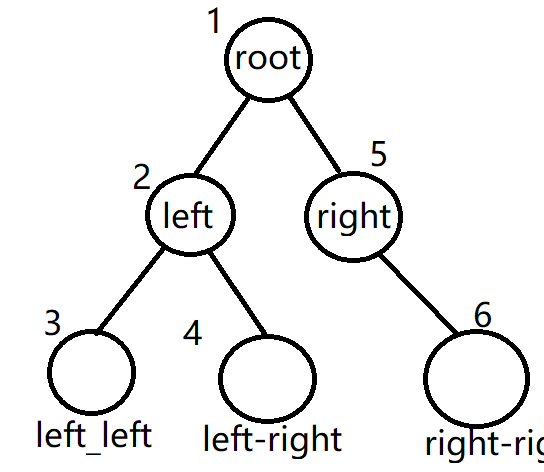
private void preOrderTraverse1(Node node){
        if(node!=null){
            System.out.println(node.getValue());
            preOrderTraverse1(node.getLeft());
            preOrderTraverse1(node.getRight());
        }
    }

2. Middle order traversal

First left subtree - > root node - > right subtree;

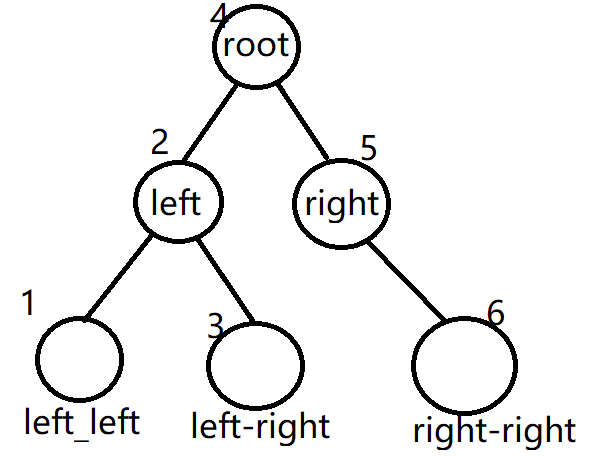
//Specific implementation of middle order traversal
    private void inOrderTraverse1(Node node){
        if(node!=null){
            inOrderTraverse1(node.getLeft());
            System.out.println(node.getValue());
            inOrderTraverse1(node.getRight());
        }
    }

3. Post order traversal

First left subtree - > right subtree - > root node;

 //Implementation of post order traversal
    private void postOrderTraverse1(Node node){
        if(node!=null){
            postOrderTraverse1(node.getLeft());
            postOrderTraverse1(node.getRight());
            System.out.println(node.getValue());
        }
    }

summary

Binary tree is a very simple and basic data structure. It is a tree structure. Learning to understand the number structure in the future is very helpful.