The key of recursive algorithm

**First of all: define the function clearly. Trust this definition. Don't * * jump into recursion.

**Secondly: * * find out what the root node wants to do, and then select the first, middle and last recursive framework according to the topic requirements.

**Finally: * * think out what each node needs to do and brush the questions.

Exercise 1: flip a binary tree

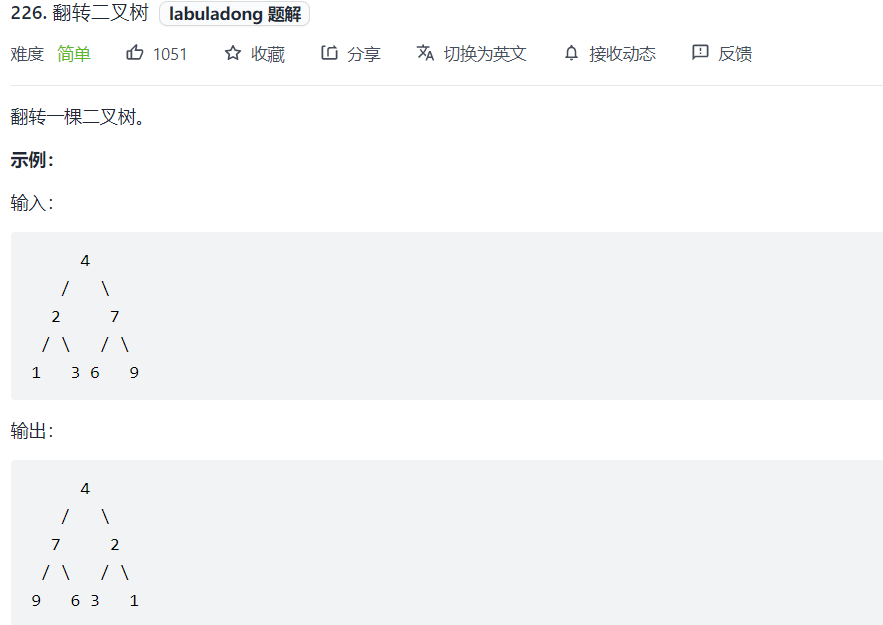
First, define the function

That is, exchange the left and right node positions of the root node and return the flipped node.

Second, make clear what you do

He wants to exchange its two child nodes, so he chooses preorder traversal

Furthermore, define what the child nodes should do

Let each child node flip their left and right child nodes.

Finally, the boundary conditions are defined

When root == null, prove that the execution has reached the leaf node, terminate the recursion and return directly.

TreeNode invertTree(TreeNode root) {
    //Judge whether the root is empty. If it is empty, return directly.
    if (root == null) {
        return root;
    }
    //Select preorder traversal
    TreeNode temp = root.left;
    root.left = root.right;
    root.right = temp;
    
    //What do the left and right nodes do? They want to exchange their left and right nodes
    invertTree(root.left);
    invertTree(root.right);
    //Return the flipped tree, root node
    return root;
}

Exercise 2: fill in the right pointer of each binary tree

The difficulty of binary tree problem is how to refine the requirements of the problem into what each node should do.

Tentative idea 1:

Like the previous question, assign the task to a node so that its left child node points to the right child node and the right child node points to null. However, we will soon find a problem. If two adjacent child nodes do not belong to a parent node, they cannot be connected. This is also the difficulty of recursion. How to refine what each node has to do.

Solution:

Refine node tasks and let two nodes undertake tasks.

Be clear about what you do

root connects its left and right child nodes.

Both the left child node and the right child node should connect their child nodes, and also connect the same layer nodes that do not belong to a root node.

Specify what the child node should do

The child node does the same thing as the parent node.

Node connect(Node root) {
    //Critical condition, if root = null, return root
    if (root == null) {
        return root;
	}
    connectTwoNode(root.left,root.right);
    return root;
}
void connectTwoNode(Node node1,Node node2) {
    //As long as one of node1 and node2 is empty, there is no need to point to it. Just keep it as it is and point to null.
    if (node1 == null || node2 == null) {
        
    }
    //Preorder traversal, pointing node1 to node2
    node1.next = ndoe2;
    //Recursively points the left child node of node1 to its right child node
    connectTwoNode(node1.left,node2.left);
    //Point the left child node of node2 to the word node
    connectTwoNode(node2.left,node2.right);
    //Point the right child node of node1 to the left child node of node2 to solve the problem of different root nodes.
    connectTwoNode(node1.right,node2.left);
}

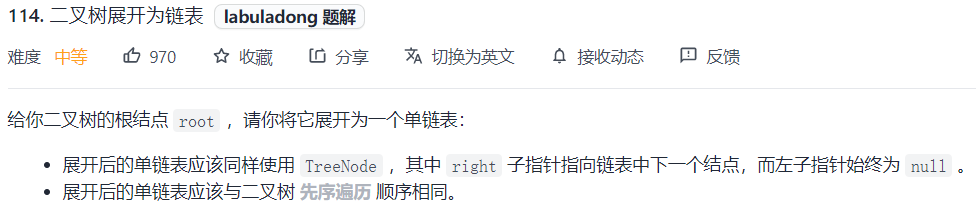
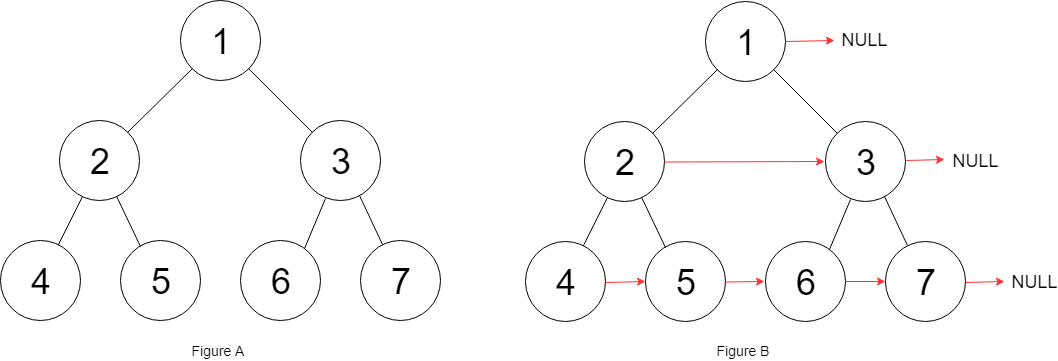
Exercise 3: expand a binary tree into a linked list

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-ostsoe81-163664365697) (C: \ users \ Axi \ appdata \ roaming \ typora \ typora user images \ image-20211107181324327. PNG)]

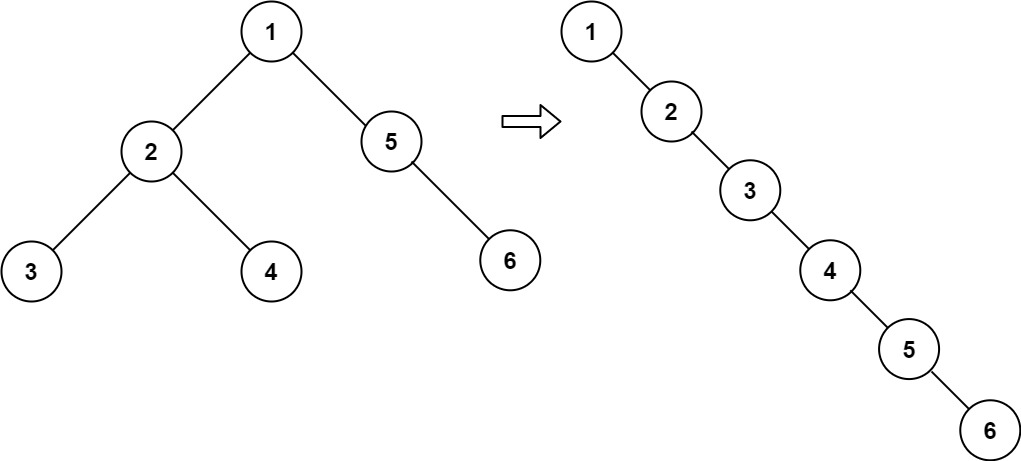
Problem solving ideas:

First, the definition of recursive function is clear

The goal is to convert its left and right subtrees into a linked list, let the left subtree replace the right subtree of the root node, and chain the original right subtree to the back of the new right subtree.

Pass in a node, and the left and right subtrees of this node are linked in the function. Therefore, post order traversal is adopted.

Be clear about what you do

Merge its left and right child nodes as described above.

Clear boundary conditions

root == null return root

The left subtree is null, and the right subtree is returned directly

The right subtree is null and is directly linked to the left subtree

public void flatten(TreeNode root) {
	if (root == null) {
        return;
    }    
    //After traversal, the left and right subtrees of the root node are linked
    flatten(root.left);
    faltten(root.right);
    //Record linked left and right subtrees
    TreeNode left = root.left;
    TreeNode right = root.right;
    //Empty left node
    root.left = null;
    //Replace the right subtree with the left subtree
    root.right = left;
    TreeNode p = root;
    //Take the left subtree as the right subtree of the root node, and chain the right subtree to the back of the original left subtree
    while (p.right != null) {
        p = p.right;
    }
    p.right = right;
    
}

Summary:

The key of recursive algorithm is to clarify the definition of function, believe this definition, and don't jump into recursive details.

The algorithm problems for writing binary trees are all based on the recursive framework. We must first find out what the root node wants to do, and then choose to use the pre order, middle order and subsequent recursive framework according to the requirements of the problem.

The difficulty of the binary tree problem is how to think about what each node needs to do through the requirements of the problem. This can only be practiced by brushing more questions.

If the three questions mentioned in this article have some inspiration for you, please connect three times. If the data is good, Dongge will brush the questions next time. You will find that the more you brush the questions of the binary tree, the more you can't stop. You can't wait to brush the questions of the binary tree in one breath.

Original link: https://labuladong.gitee.io/algo/2/18/21/

Exercise 4: constructing the largest binary tree

Clear thinking:

We determine the subscript position of the largest element in the array by traversing the maximum value in the array. According to the subscript position, we get its left and right subtrees, and then recurse the left and right subtrees to get the left and right root nodes.

Specify the function and return value of recursive function

The recursive function finds the largest element position in a given array interval, recursively finds its left and right subtrees, and returns the root node constructed with the largest element.

TreeNode constructMaximumBinaryTree(int[] nums) {
    return build(nums, 0, nums.length - 1);
}
TreeNode build(int[] nums,int left,int right) {
    //base case if left > right out of bounds
    if (left > right) {
        return null;
    }
    //Defines maxval and index to record the value and subscript of the largest element of a given range array.
    int maxVal = Integer.MIN_VALUE;
    int index = -1;
    for (int i = left ; i <= right ; i++) {
        if (nums[i] > maxVal) {
            index = i;
            maxVal = nums[i];
        }
    }
    //Creates the value of the root node based on the maximum value.
    TreeNode root = new TreeNode(maxVal);
    //Recursive construction of left subtree and right subtree
    root.left = build(nums,left,index-1);
    root.right = build(nums,index+1,right);
    //Return to root
    return root;
}

Exercise 5: constructing a binary tree by pre order and middle order

Problem solving ideas:

We need to find a way to construct the value of the head node, construct the head node, and then recursively construct its left and right subtrees.

Firstly, the principle of preorder and middle order traversal is clarified.

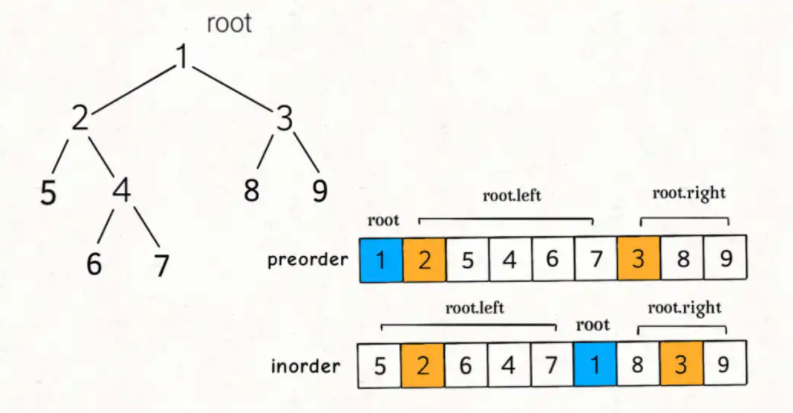
Preorder traversal: the root node is always the first element of the array. Then there are the left subtree and the right subtree.

Subsequent traversal: the root node is in the middle of the array, with the left subtree in front and the right subtree behind.

The two have the relationship of mutual utilization. If you want to restore the binary tree, they are indispensable.

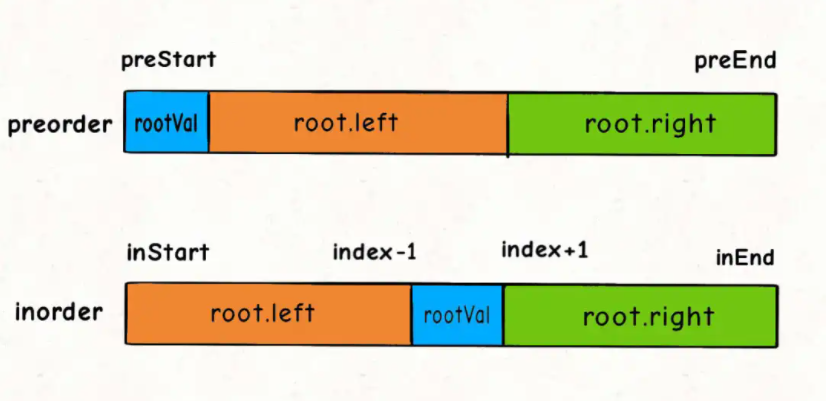
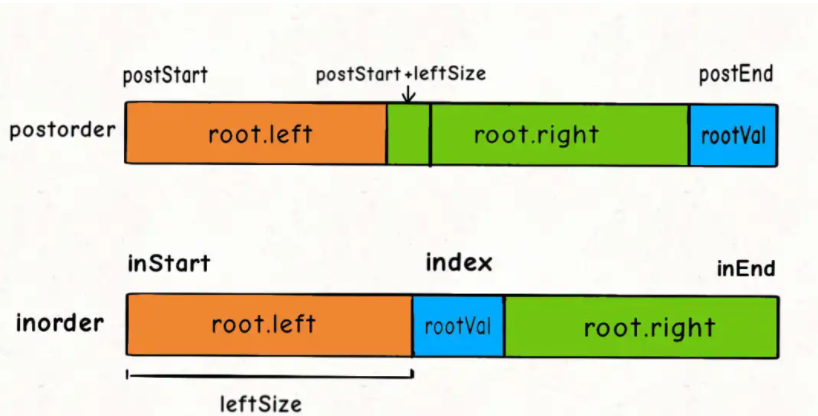
Note: leftsize is the size of the left subtree. Since preStart+leftSize contains preStart, the added size is one bit more than the original size+1, so it will be one bit more backward. Because the first place in the previous traversal is root, the size+1 just gets the area of the original lefSize.

Compare the post order traversal. Since the tail is root, the front is equivalent to taking one more bit and subtracting it.

The whole program is traversed in sequence.

Steps:

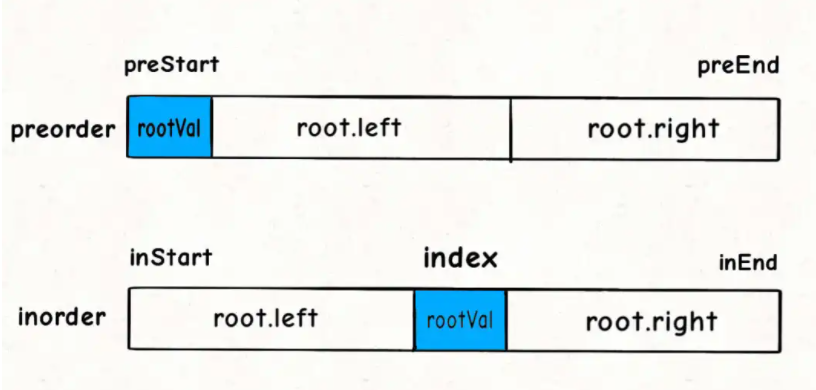
1. First, the position and value of root are obtained according to the pre order traversal
2. Find the corresponding position in the middle order according to the value of root, and record the index
3. Calculate the area occupied by the left subtree

Since the determination of the left and right sub nodes is completed by the pre order and middle order together, we need to pass in the range of the pre order and middle order traversal of the left and right sub trees to them.

class Solution {
    //It is clear that if you want to find the left and right subtrees of the root node and recursively find the root node, you need to cooperate in the first order and the middle order.
    //First, describe the following root nodes of preorder traversal and inorder traversal, as well as the positions of the left and right subtrees
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder,0,preorder.length - 1,inorder,0,inorder.length - 1);
    }
    public TreeNode build(int[] preorder,int preStart,int preEnd,int[] inorder,int inStart,int inEnd) {
        if (preStart > preEnd) {
            return null;
        }
        //First, find the root node. The position of the root node in the preorder traversal is at the 0 index
        int rootVal = preorder[preStart];
        int index = -1;
        //Find the position of the root node in the middle order traversal
        for (int i = inStart; i <= inEnd ; i++) {
            if (inorder[i] == rootVal){
                index = i;
                break;
            }    
        }
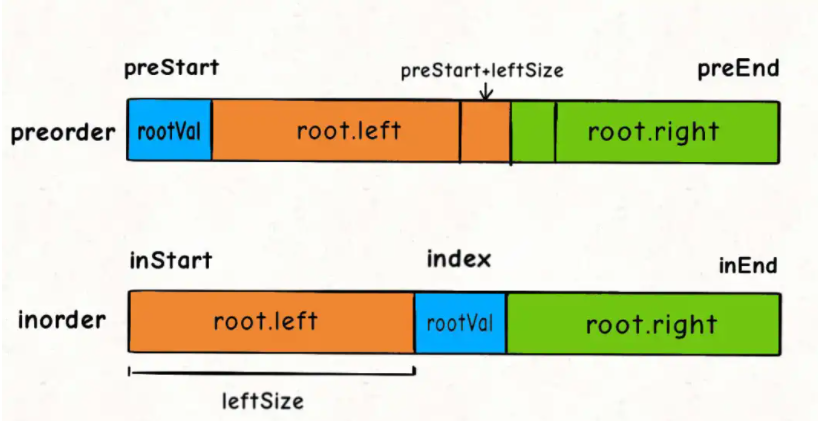
        //Record the length of the left subtree in the middle order traversal array. Because the root node is not included, it is not + 1
        int leftSize = index - inStart;
        //Construct root node
        TreeNode root = new TreeNode(rootVal);
        //Recursively construct the left and right subtrees of the root node
        root.left = build(preorder,preStart+1,preStart + leftSize,inorder,inStart,index-1);
        root.right = build(preorder,preStart + leftSize + 1,preEnd,inorder,index + 1,inEnd);
        return root;
    }
}

Exercise 6: constructing a binary tree by post order traversal

//Or the relationship of mutual restraint, we can obtain the value of the right node of the root node by post order traversal
//We can determine the position of the right node in the middle order traversal and the value of the left node.
public TreeNode buildTree(int[] inorder, int[] postorder) {
    return build(inorder,0,inorder.length - 1,postorder,0,postorder.length - 1);
}
public TreeNode build(int[] inorder,int inBegin,int inEnd,int[] postorder,int pBegin,int pEnd) {
    //base case
    if (inBegin > inEnd)
        return null;
    //The tail of the array traversed later is rootval
    int rootVal = postorder[pEnd];
    int index = 0;
    //Find the array subscript position from the middle order traversal
    for (int i = inBegin ; i <= inEnd ; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }
    //Calculate the pure leftSize without index
    int leftSize = index - inBegin;
    TreeNode root = new TreeNode(rootVal);
    //Recursively construct the left subtree of the root node. The post order traversal starts with pBegin. pBegin+leftSzie has one more bit and needs to be subtracted
    root.left = build(inorder,inBegin,index - 1,postorder,pBegin,pBegin + leftSize - 1);
    root.right = build(inorder,index + 1,inEnd,postorder,pBegin + leftSize,pEnd - 1);
    return root;
}

Exercise 7: serialization and deserialization of binary trees

Serialization is the operation of converting a data structure or object into continuous bits, and then the converted data can be stored in a file or memory. At the same time, it can also be transmitted to another computer environment through the network, and the original data can be reconstructed in the opposite way.

Please design an algorithm to realize the serialization and deserialization of binary tree. There is no restriction on the execution logic of your sequence / deserialization algorithm. You only need to ensure that a binary tree can be serialized into a string and deserialize the string into the original tree structure.

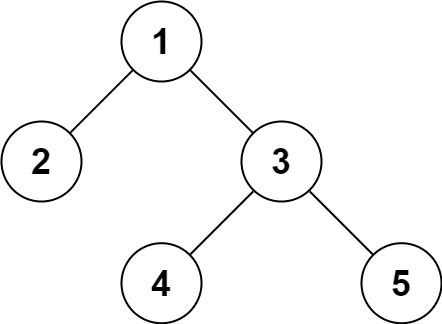
Input: root = [1,2,3,null,null,4,5]
Output:[1,2,3,null,null,4,5]

public class bianli {
    // Sequence a binary tree into a string
    public String serialize(TreeNode root) {}

    // Deserialize a string into a binary tree
    public TreeNode deserialize(String data) {}
}

Use the first method to serialize the binary tree and the second method to deserialize it.

At its root, the so-called serialization is just flattening the structured data, that is, the traversal operation of binary tree.

We use # instead of null values.

1. Preorder ergodic solution

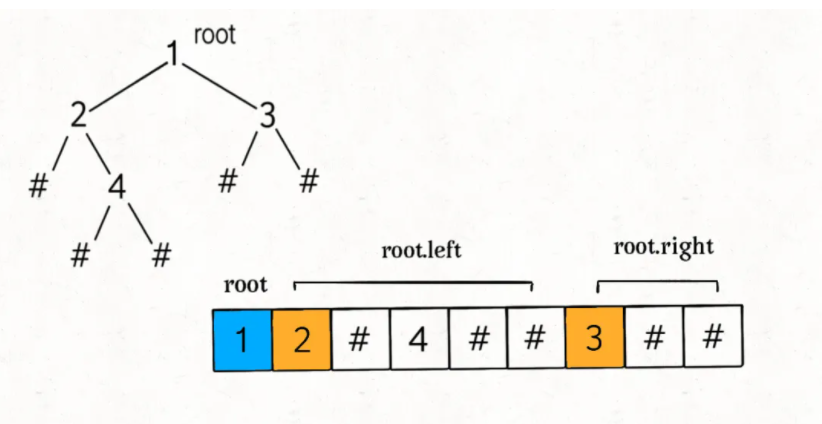
First: level the binary tree through preorder traversal.

String NULL = "#";//Use # instead of nullString SEP = ",";StringBuilder sb = new StringBuilder();// public String serialize(TreeNode root) {/ / if the root node is empty, store the null value in if (root = = null) {sb.append (null); sb.append (SEP); return null;} / / if it is not empty, add the current node into the character string, sb.append (root. VAL); sb.append (SEP) ; / / recursively serialize its left and right subtrees Serialize (root. Left); Serialize (root. Right); return sb. Tostring();}

Secondly: restore the binary tree.

We can't restore the binary tree only by preorder traversal, because we can't determine the location of null value, but we can restore the binary tree only by preorder traversal if we determine the location of null value.

public TreeNode deserialize(String data) {    //Use linked list to store node LinkedList < string > nodes = new LinkedList < > ()// Base case if (data = = null) {return null;} / / segment the string for (string node: data. Split (",") {nodes. Add (node);} 	     TreeNode root = deserialize(nodes);     return root;} Public treenode deserialize (LinkedList < string > nodes) {/ / base case if the linked list is empty, the construction ends if (nodes. Isempty()) {return null;} //Since the first node traversed by the preamble is the root node of a subtree, we might as well get its first node and remove it, so that the root node of a subtree will always be obtained during recursion. String first = nodes. Removefirst(); / / base case if the node is null, return null if (first. Equals (null)) {return null;} //Construct the root node TreeNode root = new TreeNode(Integer.parseInt(first)); / / recursively construct its left and right child nodes root.left = deserialize (nodes); root.right = deserialize (nodes); return root;}

2. Postorder ergodic solution

The difference between post order traversal and pre order traversal is shown in the following figure. Pre order traversal constructs the left subtree first and then the right subtree. This is because the root node of pre order traversal is on the left and the root node of post order traversal is on the right. Therefore, start from the right and construct the right subtree first.

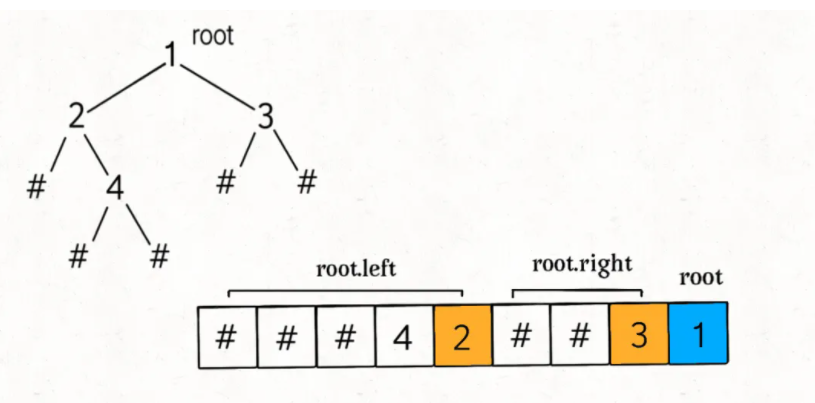
public class Codec {    String NULL = "#"; string SEP =", "; StringBuilder sb = new stringbuilder(); / / post order traversal of serialized binary tree public string Serialize (treenode root) {if (root = = null) {sb.append (null); sb.append (SEP); return null;} Serialize (root. Left); Serialize (root. Right); sb.append (root. VAL) ;        sb.append(SEP);        return sb.toString();    }    public TreeNode deserialize(String data) {        LinkedList<String> nodes = new LinkedList<>();        if (data == null) {            return null;        }        for (String node : data.split(",")) {            nodes.offer(node);        }        return build(nodes);    }     public TreeNode build(LinkedList<String> nodes) {        if (nodes.isEmpty()) {            return null;        }        String last = nodes.removeLast();        if (last.equals(NULL)) {            return null;        }        TreeNode root = new TreeNode(Integer.parseInt(last));        root.right = build(nodes);        root.left = build(nodes) ;        return root;    }}

Exercise 8: nearest common ancestor of binary tree

Given a binary tree, find the nearest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."

For example, give the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]

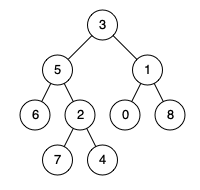
Problem solving ideas:

First: specify what the root node needs to do.

The root node first needs to know whether its left and right child nodes contain p and q (post order traversal)

Secondly: clarify the function of post order traversal

1. If the left subtree of root contains p or q and the right subtree does not, it is proved that both nodes are on the left subtree and return the first encountered node, which is their common ancestor.
2. vice versa.
3. If it is not empty, it means pq is on the opposite side of root, and you can return to root.

Because it is a post order traversal, the first accessed node is the leaf node, so the root satisfying the condition for the first time is the nearest ancestor.

Finally: specify the base case

1. root == null directly returns null
2. root == p or root == q according to the topic, both p and Q are in the binary tree with root node, so root is their nearest common ancestor.

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {    //If the root is null, it will directly return null when it reaches the leaf node. / / if the root = = P / Q, P or q is their nearest public ancestor. If (root = = null | root = = P | root = = q) {return root;} / / perform a post order traversal. Before you know what the root node needs to do, specify the status of the left and right subtrees. Treenode left = lowestcommonprocessor (root.left, P, q); TreeNode right = lowestCommonAncestor(root.right,p,q);    // If the left subtree is empty, that is, there are no P and Q, it is proved that the nodes are all on the right subtree, and the node found by the right subtree first is the ancestor 		 First. vice versa. If (left = = null) {return right;} else if (right = = null) {return left;} / / both are empty. It is proved that they are on the opposite side. Just return root. else {        return root;    }}

Exercise 9: binary tree pruning

Give you the root node of the binary tree, root. In addition, the value of each node of the tree is either 0 or 1.

Returns the original binary tree with all subtrees that do not contain 1 removed.

The subtree of a node is the node itself plus the descendants of all nodes.

Problem solving ideas:

Specify what the root node should do

The root node makes decisions based on whether its left and right child nodes contain 1 and whether its own value is 0. (post order traversal)

public TreeNode pruneTree(TreeNode root) {    //Using post order traversal, we can know whether this tree contains 1 only if we know whether the left and right subtrees contain 1. If (root = = null) {return null;} / / recursively assign the left and right subtrees of root root root.left = prunetree (root. Left); root.right = pruneTree(root.right);    // If the left or right subtree is null and the value of the node is 0, it means that the subtree including the node does not contain the node with value 1, 	  Empty. if (root.left == null && root.right == null && root.val == 0) {        return null;    }    return root;}

Exercise 10: printing a binary tree from top to bottom

Investigating binary tree sequence traversal

class Solution {    public List<List<Integer>> levelOrder(TreeNode root) {        //Base case if (root = = null) {return new arraylist();} / / install the root node with a queue queue < treenode > queue = new arraydeque < > (); 	// Loading result list < list < integer > > Print = new ArrayList < > (); queue.offer(root);// Queue the root node first while (!queue.isEmpty()) {/ / if the queue is empty, the printing is completed. int count = queue.size(); / / record the number of nodes in each layer. List < integer > prints = new ArrayList < > (); / / load the printed nodes in each layer. / / loop through the nodes in each layer. While (count > 0) {treenode node = queue. Poll(); / / out of queue prints.add(node.val); 	// Add the current node to the print list if (node. Left! = null) {/ / if the left subtree is not empty, queue. Offer (node. Left);} if (node. Right! = null) {queue. Offer (node. Right);} count --; / / subtract} print.add(prints);        }        return print;    }}

Exercise 11: symmetric binary tree

Given a binary tree, check whether it is mirror symmetric.

For example, a binary tree [1,2,2,3,4,4,3] is symmetric.

    1   / \  2   2 / \ / \3  4 4  3

However, the following [1,2,2,null,3,null,3] is not mirror symmetric:

    1   / \  2   2   \   \   3    3

1. Recursive implementation

First, clarify what the root node does.

The root node and itself are symmetrical. If the tree wants to be symmetrical, the left and right subtrees of the root node need to be symmetrical. The conditions that determine the symmetry of the left and right subtrees of the root node are that the left subtree and the right subtree of the left subtree are symmetrical, and the right subtree of the left subtree and the left subtree of the right subtree are symmetrical.

Secondly, define the base case

1. When the root node is null, the tree is symmetric.

2. The left child node is null and the right child node is not null. Conversely, the tree is not symmetrical.

3. The left and right child nodes of the root node must be symmetrical.

Left and right node symmetry & & the left node of the left node is symmetrical with the right node of the right node & & the right node of the left node is symmetrical with the left node of the right node

public boolean isSymmetric(TreeNode root) {    //base case    if (root == null) return true;    return recur(root.left,root.right);}public boolean recur(TreeNode node1,TreeNode node2) {    //base case    if (node1 == null && node2 == null) {        return true;    }    if (node1 == null) {        if (node2 != null) return false;    }    if (node2 == null) {        if (node1 != null) return false;    }     return (node1.val == node2.val) && recur(node1.left,node2.right) && recur(node1.right,node2.left);}

2. Iterative implementation

When we iterate, we usually introduce a queue, which is a common method to turn recursion into iteration.

First, we queue the root node twice, iterating out the left and right child nodes of the queue each time to judge whether they are all empty. If not, one is empty and the other is not empty, asymmetric, different values, asymmetric.

We store their left and right sub nodes separately. The left sub tree of the left sub node and the right sub tree of the right sub node are stored together, and the right sub tree of the left sub node and the left sub tree of the right sub node are stored together. This is to judge whether they are symmetrical.

End of cycle, symmetry.

public boolean isSymmetric(TreeNode root) {    Queue<TreeNode> queue = new LinkedList<>();    queue.offer(root);    queue.offer(root);    while (!queue.isEmpty()) {        TreeNode left = queue.poll();        TreeNode right = queue.poll();        if (left==null && right ==null) continue;        if ((left == null || right == null) || left.val != right.val) {            return false;        }        queue.offer(left.left);        queue.offer(right.right);        queue.offer(left.right);        queue.offer(right.left);    }    return true;}