preface

In the previous data structure blog post, we have learned about the basic binary tree, but today we will explain in detail the traversal of chain binary tree and various operations.
The learning of chain binary tree can exercise our recursive thought and divide and conquer thought very well.

Definition of chain binary tree

How to define a chained binary tree?
We use a structure to represent a node of a binary tree, in which a variable stores the value of the binary tree node, and two pointers to this structure store the addresses of its left and right nodes. The code is as follows:

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

Traversal of chained binary tree

Preorder traversal

The mantra of preorder traversal is "about the root". Its idea is to visit the root of the tree first, then the left child of the number, and finally the right node of the tree. For example, the binary tree as shown in the figure:

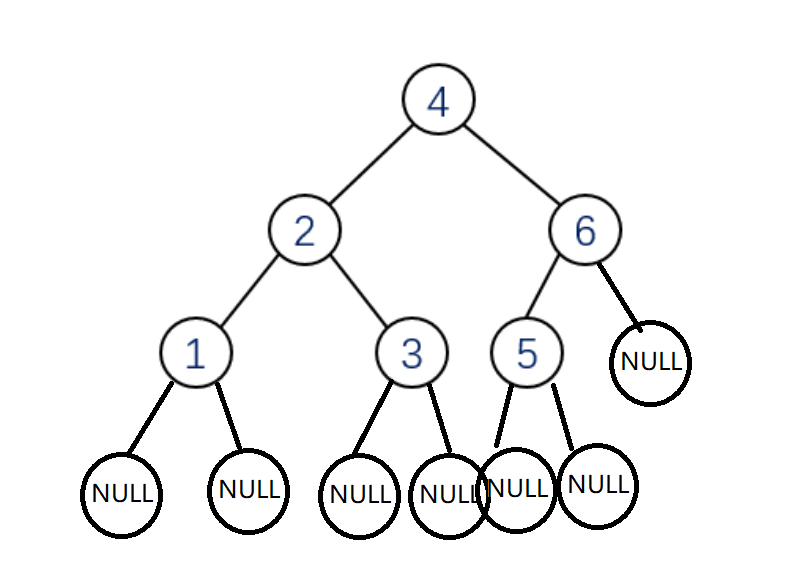
Traversal process:
We first access its root, i.e. 4, and then access its left child 2. The left child 2 starts from its own 2 as the root, and then accesses the left child 1 of 2. The left child 1 as the root, first accesses its own 1, and then returns to 1 if the left child is NULL, and then returns to 1 if the right child of 1 is NULL, and so on. The traversal order is:

4， 2， 1， 3， 6， 5
code:

void PrevOrder(BTNode* root)
{
	if(root == NULL)
	{
		printf("NULL");
		return;
	}
	printf("%d ",root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

Middle order traversal

The middle order traversal is similar to the front order traversal, except that it first traverses the left subtree, then traverses the root, and finally traverses the right subtree. The formula is left root and right. The code is as follows

void InOrder(BTNode* root)
{
	if(root == NULL)
	{
		printf("NULL");
		return;
	}
	InOrder(root->left);
	printf("%d ",root->data);
	InOrder(root->right);
}

Postorder traversal

Post order traversal is to traverse the left subtree of the tree first, then the right subtree, and finally the root. The formula is the left and right roots. The code is as follows:

void PostOrder(BTNode* root)
{
	if(root == NULL)
	{
		printf("NULL");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ",root->data);
}

level traversal

Sequence traversal is from the first node of the first layer to the second layer, and each layer traverses from left to right.

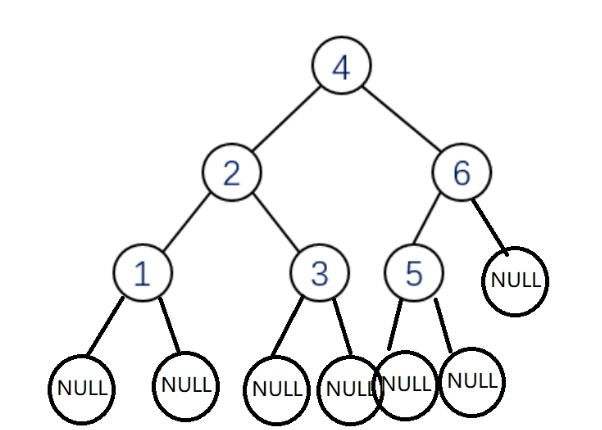
Taking this tree as an example, its sequence traversal result is:
4 2 6 1 3 5
How do you implement this code?
Here we will use a data structure queue.
Our method starts from the root node, first queue the root node, then traverse a node, queue its left subtree, and then queue its right subtree. NULL does not queue until the queue is empty. The code is as follows:

void LevelOrder(BTNode* root)
{
	if(root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while(!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->data);
		if(front->left != NULL)
		{
			QueuePush(&q,root->left);
		}
		if(front->right!= NULL)
		{
			QueuePush(&q,root->right);
		}
	}
	QueueDestroy(&q);
}

Find the number of nodes of the binary tree

Just find the number of nodes and divide and conquer directly
If the parent node is not empty, add one; if it is empty, add 0;
The code is as follows:

int BinTreeSize(BTNode* root)
{
	return root == NULL ? 0 : (1 + BinTreeSize(root->left) + BinTreeSize(root->right));
}

Find the number of leaf nodes of binary tree

First, we need to know how to judge leaf nodes:
Nodes with empty left and right subtrees are leaf nodes. So we can judge according to this property. The code is as follows:

int BinTreeLeafSize(BTNode* root)
{
	if(root == NULL)
	{
		return 0;
	}
	return root->left == NULL && root->right == NULL ? 1 : BinTreeLeafSize(root->left) + BinTreeLeafSize(root->right);
}

Find the number of nodes in the K-th layer of the binary tree

The idea is: if the current node is layer k, add one. If not, recurse to the next layer and let k - 1

int BinTreeLevelKSize(BTNode* root, int k)
{
	if(root == NULL)
	{
		return 0;
	}
	if(k == 1)
	{
		return 1;
	}
	return BinTreeLevelKSize(root->left, k-1) + BinTreeLevelKSize(root->right, k-1);
}

Find the maximum depth of binary tree

To simplify this problem is to find the larger depth of the left and right subtrees, and then add 1 Because the root node itself also occupies a depth.
The code is as follows:

int BinTreeDepth(BTNode* root)
{
	if(root == NULL)
	{
		return 0;
	}
	int leftDepth = BinTreeDepth(root->left);
	int rightDepth = BinTreeDepth(root->right);
	return leftDepth > rightDepth ? leftDepth + 1 : rigthDepth + 1;
}

Give a number to return to the node

The idea is to find the node from its left and right subtrees until it is found.
The code is as follows:

BTNode* BinTreeNodeFint(BTNode* root, BTNDataType x)
{
	if(root == NULL)
	{
		return NULL;
	}
	if(root->data == x)
	{
		return root;
	}
	BTNode* Left = BinTreeNodeFint(root->left, x);
	if(Left != NULL)
	{
		return Left;
	}
	BTNode* Right = BinTreeNodeFint(root->right, x);
	if(Left != NULL)
	{
		return Right ;
	}
	return NULL;
}

Judge whether the number is a complete binary tree

The judgment of complete binary tree is that there can be no empty nodes in the process of sequence traversal until the end of the number, which is a complete binary tree.
The code is as follows:

bool BinTreeComplete(BTNode* root)
{
	if(root == NULL)
	{
		return true;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while(!QueueEmpty(&q))
	{
		BTNode* Front = QueueFront(&q);
		QueuePop(&q);
		if(Front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	while(!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&a);
		QueuePop(&q);
		if(front == NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

Destruction of binary tree

The destruction of binary tree must be traversed in later order, otherwise if the root is destroyed first, the left and right nodes will not be found
The code is as follows:

void BinTreeDestroy(BTNode* root)
{
	if(root == NULL)
	{
		return;
	}
	BinTreeDestroy(root->left);
	BinTreeDestroy(root->right);
	free(root);
}