tree

Array, linked list and tree storage

Analysis of array storage mode
   advantages: it is fast to access elements by subscript. For ordered arrays, binary search can also be used to improve the retrieval speed.
   disadvantages: if you want to retrieve a specific value, or the inserted value (in a certain order) will move as a whole, which is inefficient

Analysis of chain storage mode
   advantages: the array storage mode is optimized to a certain extent (for example, if you insert a numeric node, you only need to link the inserted node to the linked list, and the deletion efficiency is also very good).
   disadvantages: the efficiency is still low when retrieving, for example (to retrieve a value, you need to traverse from the beginning of the node)

Analysis of tree storage mode
   it can improve the efficiency of data storage and reading. For example, using binary sort tree can not only ensure the speed of data retrieval, but also ensure the speed of data insertion, deletion and modification.

Common terms for trees

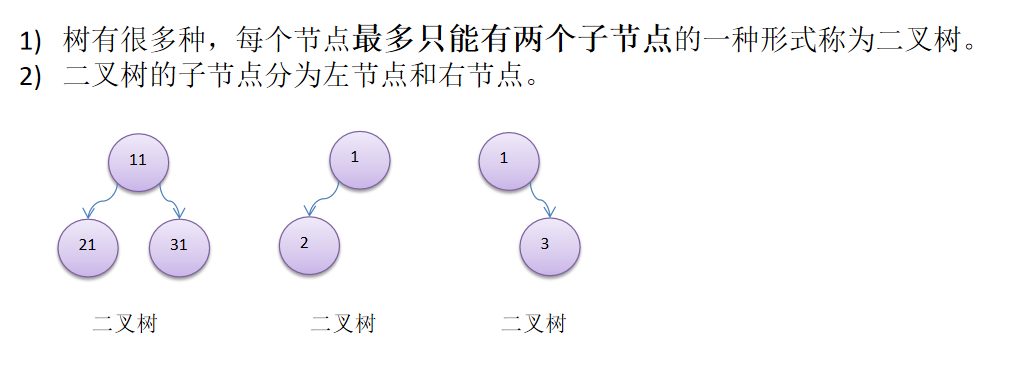
Binary tree

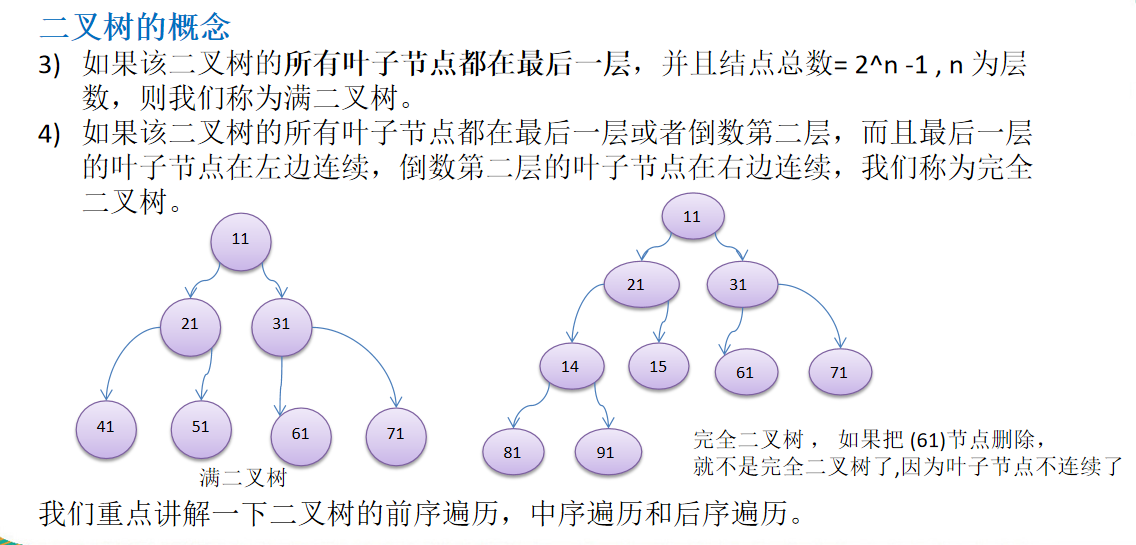
Full binary tree, complete binary tree

Traversal of binary tree

thinking

• Preorder traversal: first output the parent node, and then traverse the left and right subtrees
• Middle order traversal: first traverse the left subtree, then output the parent node, and then traverse the right subtree
• Post order traversal: first traverse the left subtree, then traverse the right subtree, and finally output the parent node
• Summary: see the order of output parent nodes to determine whether it is pre order, middle order or post order

Preorder traversal

class BinaryTree{
    public void perOrder(){
        if(root!=null){
            root.preOrder();
        }else{
            System.out.println("The tree is empty");
        }
    }
}

class Node{
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }
}

Medium order traversal

class BinaryTree{
    public void midOrder(){
        if(root!=null){
            root.midOrder();
        }else{
            System.out.println("The tree is empty");
        }
    }
}

class Node{
    public void midOrder(){
        if(this.left!=null){
            this.left.midOrder();
        }
        System.out.println(this);
        if(this.right!=null){
            this.right.midOrder();
        }
    }
}

Postorder traversal

class BinaryTree{
    public void behindOrder(){
        if(root!=null){
            root.behindOrder();
        }else{
            System.out.println("The tree is empty");
        }
    }
}

class Node{
    public void behindOrder(){
        if(this.left!=null){
            this.left.behindOrder();
        }

        if(this.right!=null){
            this.right.behindOrder();
        }

        System.out.println(this);
    }
}

Front, middle and back lookup of binary tree

thinking

Preorder search

    public HeroNode perSearch(int no){
        if(this.no == no){
            return this;
        }

        HeroNode resNode = null;
        if(this.left != null){
            resNode = this.left.perSearch(no);
        }
        if(resNode!=null){
            return resNode;
        }
        if(this.right!=null){
            resNode = this.right.perSearch(no);
        }
        return resNode;

    }

Middle order search

    public HeroNode midSearch(int no){
        HeroNode resNode = null;
        if(this.left !=null){
            resNode = this.left.midSearch(no);
        }
        if(resNode!=null) {
            return resNode;
        }

        if(this.no == no){
            return this;
        }

        if(this.right!=null){
            resNode = this.right.midSearch(no);
        }

        return resNode;
    }

Sequential search

    public HeroNode behindSearch(int no){
        HeroNode resNode = null;
        if(this.left!=null){
            resNode = this.left.behindSearch(no);
        }
        if(resNode!=null){
            return resNode;
        }

        if(this.right!=null){
            resNode = this.right.behindSearch(no);
        }
        if(resNode!=null){
            return resNode;
        }

        if(this.no == no){
            return this;
        }

        return resNode;
    }

Delete node

thinking

code

    public void delNode(int no){
        if(this.left!=null&&this.left.no == no){
            this.left = null;
            return;
        }

        if(this.right!=null&& this.right.no==no){
            this.right=null;
            return;
        }

        if(this.left!=null) this.left.delNode(no);
        if(this.right!=null) this.right.delNode(no);
    }
    

Sequential storage binary tree

Introduction:

Train of thought; (store the binary tree as an array)

Scenario: heap sorting

code:

public class _Sequential storage binary tree_ {
    public static void main(String[] args){
        int arr[] = {1,2,3,4,5,6,7};
        ArrayBinaryTree abt = new ArrayBinaryTree(arr);
        abt.perOrder();
    }
}


class ArrayBinaryTree{
    private int []arr;

    public ArrayBinaryTree(int []arr){
        this.arr = arr;
    }

    public void perOrder(){
        this.perOrder(0);
    }

    // Write a method to complete the preorder traversal of the sequential stored binary tree
    public void perOrder(int index){ // Represents an array subscript
        // If the array is empty, or arr.length = 0
        if(arr.length==0|| arr ==null){
            System.out.println("The array is empty and cannot be traversed in sequence");
        }
        // Output current element
        System.out.print(arr[index]+"\t");
        // Left recursive traversal
        if(index*2+1<arr.length) perOrder(index*2+1);
        // Right recursive traversal
        if(index*2+2<arr.length) perOrder(index*2+2);

    }
}

Cued binary tree

introduce

The empty finger domain of the tree is used to make them point to the precursor nodes and subsequent nodes in a certain traversal order

Medium order cued binary tree

Idea:

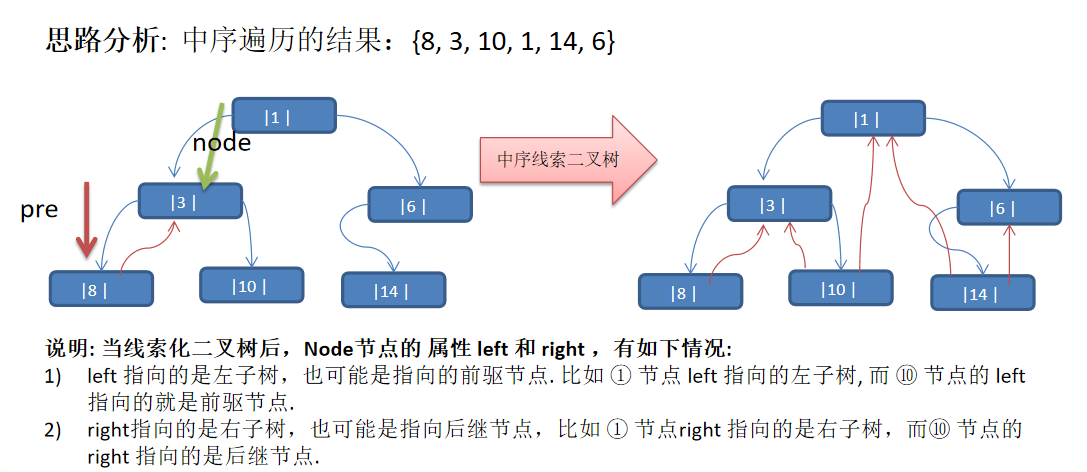
code:

class ThreadedBinaryTree{
    private HeroNode root;
    private HeroNode pre = null;// pre keeps the previous node
    
    // Write the code for medium order cueing of binary tree
    // Node: the node that currently needs to be threaded
    public void threadedNodes(HeroNode node){
        if(node==null){
            System.out.println("No clue");
            return;
        }
        /*
        Cue preamble node
        Cue current node
        Cued successor node
         */
        threadedNodes(node.getLeft());
        if(node.getLeft() == null){
            node.setLeft(pre);
            node.setLeftType(1);
        }

        if(pre!=null&&pre.getRight()==null){
            // Let the right pointer of the predecessor node point to the current node
            pre.setRight(node);
            pre.setRightType(1);
        }
        // After each node is processed, the current node is the precursor node of the next node
        pre = node;

        threadedNodes(node.getRight());
        
    }
}    

class HeroNode{
    private HeroNode left;
    private HeroNode right;
    // explain:
    // 1. If leftType == 0, it indicates the left child node. If 1 is the precursor node
    // 2. If rightType == 0, it indicates the right subtree, and 1 is the successor node
    private int leftType;
    private int rightType;

    public int getLeftType() {
        return leftType;
    }

    public void setLeftType(int leftType) {
        this.leftType = leftType;
    }

    public int getRightType() {
        return rightType;
    }

    public void setRightType(int rightType) {
        this.rightType = rightType;
    }
}