This column is a summary of my learning code Capriccio binary tree. Part of the content comes from the website https://programmercarl.com/ (code Capriccio)

2 binary tree traversal

2.1 depth first traversal DFS

Depth first traversal refers to traversing in one direction first and then going back to the other direction. Depth first traversal is divided into pre order traversal, middle order traversal and post order traversal. The difference is:

Traversal mode	Traversal direction	explain
Preorder traversal	Middle left and right	First traverse the middle node, then traverse the left and then the right
Medium order traversal	Left middle right	First traverse the left node, then the middle node, and then the right node
Postorder traversal	Zuo Youzhong	First traverse the left node, then the right node, and then the middle node

It can be seen that to distinguish which traversal mode is literally the position in the, a specific example

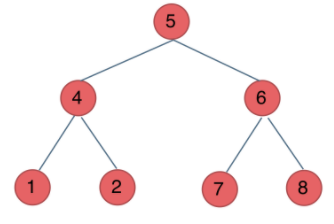
Preorder traversal: middle left and right 5412678
Middle order traversal: left middle right 1425768
Subsequent traversal: left and right middle 1247865

2.2 implementation of depth first traversal code

2.2.1 recursive implementation

Recursive implementation is a simple way. The difference between the three traversals is only to read the code position of the current node

This question is the 144th question of leetcode. As long as you change the position of the code put into the vector, you can change the traversal order. Why do you write a recursive function again instead of directly recursive in the previous function? The reason is that because we need to traverse the whole tree, we can't return the value when we encounter an empty node. Instead, we can get the return value only after all traversals. Therefore, we can rewrite a recursive function and directly return null.
According to the description in the code recall website, when we meet the conditions and return, we need the return value of the recursive function. On the contrary, when we need to traverse the whole tree, we don't need the return value, but when we need to change the tree structure, we still need the return value even if the conditions are met. At this time, we use a variable to receive the return value instead of directly return.

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        traversal(root);
        return ret;
    }
private:
    vector<int> ret;
    void traversal(TreeNode *node) {
        if (node == nullptr) return;

        ret.push_back(node->val);      // Preorder traversal
        traversal(node->left);
        // ret.push_ back(node->val);   //  Medium order traversal
        traversal(node->right);
        // ret.push_ back(node->val);   //  Postorder traversal
    }
};

2.2.2 iterative method for traversal

Recursion is actually a process of pressing stack and out of stack, so stack can be used to simulate this process
First, stack the right node and stack the left node. In this way, the left node is the first to be out of the stack. At this time, the processing node is also the middle node of the next tree.
As long as you invert the obtained array, you can get the post order traversal, which is different from the middle order traversal.

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ret;
        if (root == nullptr) return ret;
        stack<TreeNode*> nodeStack;
        nodeStack.push(root);
        while (!nodeStack.empty()) {
            auto currNode = nodeStack.top();
            nodeStack.pop(); // Out of stack
            ret.push_back(currNode->val); // Current node, in

            if (currNode->right != nullptr) nodeStack.push(currNode->right);    // right
            if(currNode->left != nullptr) nodeStack.push(currNode->left);       // Left
        }
        return ret;
    }
};

Middle order traversal code implementation

As mentioned above, the middle order code is slightly different from the pre order / post order code because the node directly processed during the pre order is the intermediate node, while the middle order traversal needs to process the left node first. Therefore, the modified code is as follows:

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> nodeStack;
        auto currNode = root;
        while (currNode != nullptr || !nodeStack.empty()) {
            if (currNode != nullptr) {
                nodeStack.push(currNode);
                currNode = currNode->left;
            } else {
                currNode = nodeStack.top();
                nodeStack.pop();
                ret.push_back(currNode->val);   // Left node
                currNode = currNode->right;     // Right node
            }
        }

        return ret;
    }
};

2.3 sequence traversal

Sequence traversal is actually breadth first traversal, which is different from depth first traversal. There is only one traversal mode for sequence traversal, that is, layer by layer from left to right. The code uses the idea of queue

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ret;
        if (root == nullptr) return ret;
        queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);  // Put the root node into
        while (!nodeQueue.empty()) {
            vector<int> path;
            for (int i = nodeQueue.size(); i > 0; --i) { // Nodequeue. Cannot be used here Size () as a condition, because it will change
                auto currNode = nodeQueue.front();
                nodeQueue.pop();
                path.push_back(currNode->val);
                if (currNode->left) nodeQueue.push(currNode->left);
                if (currNode->right) nodeQueue.push(currNode->right);
            }
            ret.push_back(path);
        }
        return ret;
    }
};