subject

analysis

This is a typical example of dynamic programming. The optimal substructure should be selected at each step, that is, the lattice that can get the most gold coins.

Here are two ideas to solve this problem: backtracking and dp array. These two ideas can be said to find the optimal solution in the opposite way, one from top to bottom and the other from bottom to top.

to flash back

We start at the starting point (0,0) and either go down or go right. The only condition for deciding whether to go right or down is to see which position can get more gold coins at the end and who can get more gold coins on which side. Similarly, in the next position, judge whether to go down or right in the same way until you reach the end position (n-1,n-1).

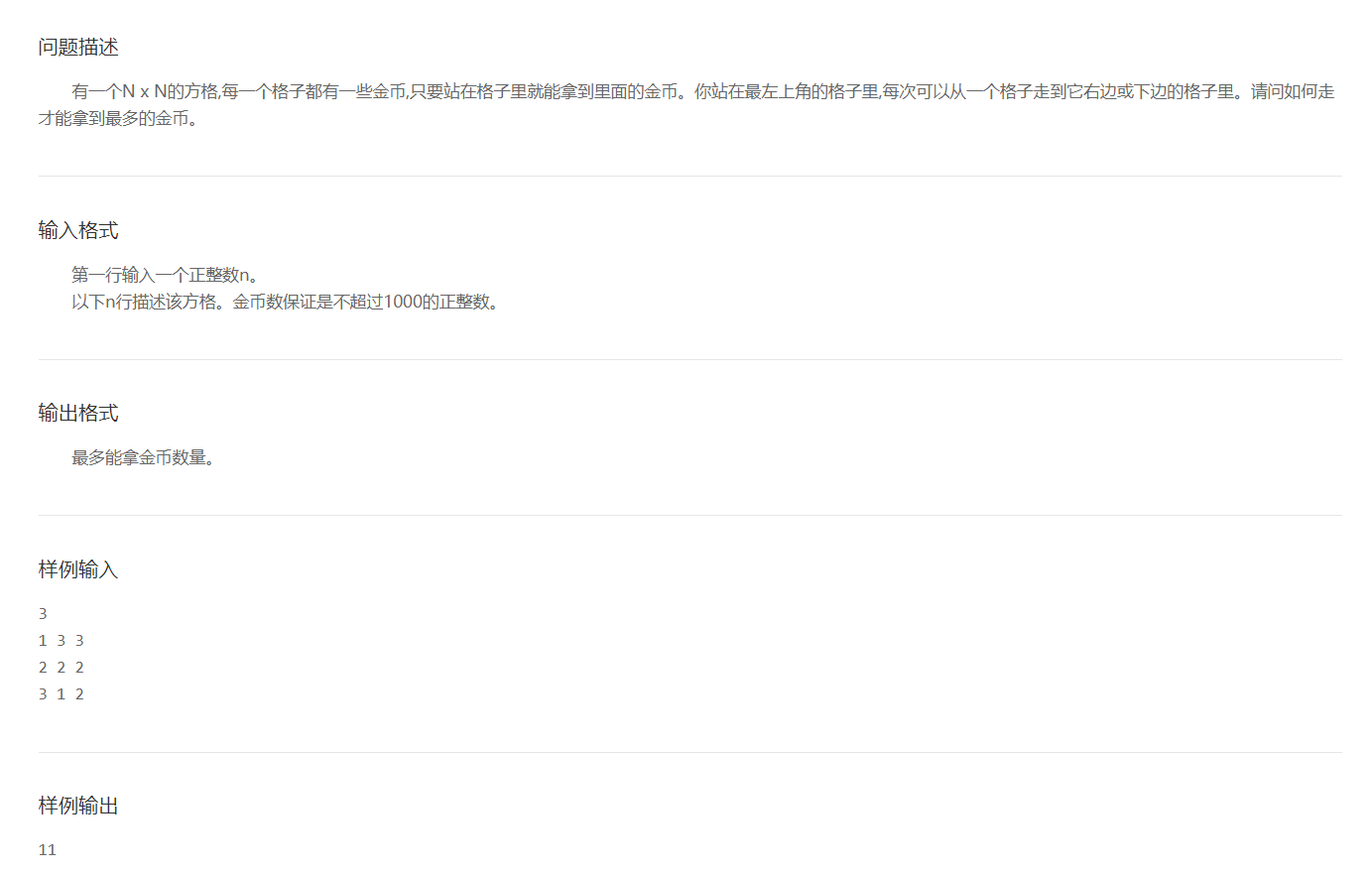
After reaching the end position (2,2) (if n is 3 in 3 rows and 3 columns), the recursion will not continue, and the value here will be told to (2,1) and (1,2). Then the number of gold coins you can get from position (2,1) to the end is 1 + 2 = 3, and the number of gold coins you can get from position (1,2) to the end is 2 + 2 = 4. For position (1,1), it can choose to go down, go to position (1,2), or go right to position (2,1), because you can get more gold coins from position (1,2) to the end position, so position (1,1) should choose to go from grid (1,2) to the end point, and repeat the above operation until the starting point (0,0) can also decide whether to choose to go down or right, Finally, the maximum number of gold coins will be returned as the result.

However, if we look at the above figure, we can find that there are many locations that have been repeatedly passed (for example, (1,1), (2,1), (1,2)), so it is not necessary to go through the road again. We can use the tag array to record the passing positions to achieve pruning and improve the execution efficiency.

Now let's look at the code implementation:

def dfs(x,y):
    # The position outside the range of n rows and n columns is meaningless. End the recursion
    if x > n-1 or y > n-1:
        return 0
    # Go to the end position and return the gold coins at the end position
    if x == n-1 and y == n-1:
        return nums[x][y]
    # If you don't walk through this position, record it. If you walk to the same position next time, you can return the result in advance
    if not used[x][y]:
        # If you go down, you can get more gold coins or go to the right. You can go wherever you get more,
        # Then add the number of gold coins in this position
        # Then, after several layers of recursion, you can get the maximum number of gold coins from this position to the end
        used[x][y] = max(dfs(x+1,y),dfs(x,y+1)) + nums[x][y]
    return used[x][y]
    
    
n = int(input())
nums = []
for i in range(n):
    nums.append(list(map(int,input().split())))
# Define tag array
used = [[0 for i in range(n)] for j in range(n)]
# Return recursive results
print(dfs(0,0))

I have debugged the above code many times and tried many cases without finding any problems... But I can only get 30 points for submitting the code, and the answers to the errors are the answers to the errors, not the running timeout. After thinking for a long time, I still haven't found the problem, and I can only see the sample vip... It's like dying in peace 😭😭

I hope you can give me some advice. Thank you very much!

The following DP can get full marks. Let's take a look at the following.

DP

DP array can be said to be a major feature of dynamic programming, because too many problems of dynamic programming can be solved by DP array, and the most commonly used one is two-dimensional array.

We can use DP [i] [j] to indicate the maximum number of gold coins we can get from the starting point to row I and column j. Pay attention to distinguish it from the idea of backtracking algorithm above.

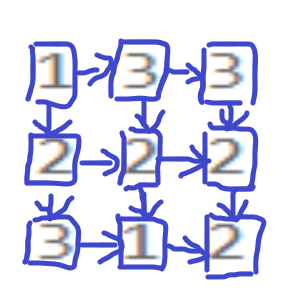
We know that a square can come from above it or from his left. As for which side you come from, it depends on which side has got more gold coins and which side has got more gold coins. Repeat the above steps continuously. When you reach the end position (2,2), you can know the maximum number of gold coins you can get.

If you want to go to position (1,1), it can come from two positions (0,1), (1,0). To determine which side to come from, it depends on which side has received more gold coins and which side has received more gold coins. Obviously, (0,1) position has got 1 + 3 = 4 gold coins, which will be more. If you want to go to (1,1) position, you have to go from (0,1).

In general, a position needs to judge whether to come from the left or the top of the position, but there are also special cases, that is, the leftmost and uppermost positions.

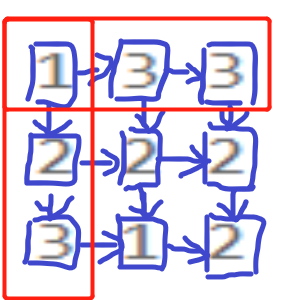
If you want to go to the red squares on the left, you must come from the top of these squares. (for example, if you want to go to (0,2), you must come from (0,1). Similarly, if you want to go to the squares marked red above, you must come from the left of these squares. In the above two cases, only one side needs to be considered,

For the middle square, you need to know the number of gold coins in the left and upper squares before you can choose which side to come from according to which side to get more gold coins. Therefore, when calculating the maximum number of gold coins that can be obtained in the middle square, we need to know the maximum number of gold coins that can be obtained on the leftmost and uppermost sides first, so that the middle square can know whether to come from the left or the top.

Let's look at the code implementation:

nums = []
n = int(input())
for i in range(n):
    nums.append(list(map(int, input().split())))

# Initialize the dp array and set it all to 0 first
dp = [[0 for i in range(n)] for j in range(n)]
# Get the number of starting gold coins
dp[0][0] = nums[0][0]
# First find out the number of gold coins you can get in the leftmost and uppermost squares. There is no maximum number of gold coins here, because you have no choice
for i in range(1, n):
    # The number of gold coins that can be obtained in the top square is the number of gold coins that can be obtained in the left square plus the number of gold coins that can be obtained from each position
    dp[i][0] = dp[i - 1][0] + nums[i][0]
    # The number of gold coins that can be obtained in the leftmost square is the number of gold coins that can be obtained in the upper square plus the number of gold coins that can be obtained from each position
    dp[0][i] = dp[0][i - 1] + nums[0][i]

# Now is the maximum number of gold coins that can be obtained in the middle square
for i in range(1, n):
    for j in range(1, n):
        #  Either choose the upper side or the left side. Whichever side has more money comes from. After the selection, add the number of gold coins you can get from each position as the maximum number of gold coins from the starting point to this position
        dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + nums[i][j]
        
# After executing the above procedure, the maximum number of gold coins that each square can get in the sequence of n x n has been recorded
# The maximum number of gold coins you can get when you return to the destination
print(dp[n - 1][n - 1])