Question 1: the week at the end of the century
Title Description
A cult once called December 31, 1999 the end of the world. Of course, the rumor has been broken. Others say that December 31 at the end of a century in the future, if it is Monday, it will
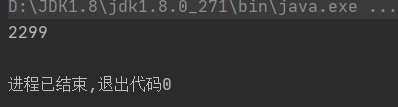
Interestingly, December 31 of any year at the end of the century cannot be Monday!! Therefore, the "rumor manufacturer" is revised to Sunday... December 31, 1999 is Friday. May I ask: which December 31 at the end of the century (i.e. xx99) closest to us in the future happens to be Sunday (i.e. Sunday)?
Please answer the year (only write this 4-digit integer, do not write redundant information such as December 31)
The code is as follows:
package java_b2013;
public class Main1 {
static int [] time ={1,2,3,4,5,6,7};
public static void main(String[] args) {
int day=0;
for (int i=2000;;i++) {
if(i%4==0 && i%100==0 || i%400==0){
day+=366;
}else {
day+=365;
}
if((day+5)%7==0 && (i-99)%100==0){
System.out.println(i);
return;
}
}
}
}
Operation results:
Question 2: careless formula
Title Description
Xiao Ming is an acute child. When he was in primary school, he often copied the questions written by the teacher on the blackboard wrong. Once, the teacher's question was: 36 x 495 =? He copied it: 396 x 45 =? But the result is very dramatic. His answer is actually right!! Because 36 * 495 = 396 * 45 = 17820, there may be many similar coincidence situations. For example, 27 * 594 = 297 * 54 how many formulas such as ab * cde = adb * ce can be satisfied if a b c d e represents 5 different numbers from 1 to 9 (note that they are different numbers and do not contain 0)? Please use the advantages of computers to find all the possibilities and answer the types of different formulas. The formulas satisfying the commutative law of multiplication are of different kinds, so the answer must be an even number.
The code is as follows:
package java_b2013;
import java.util.HashMap;
import java.util.HashSet;
public class Main2 {
static HashSet<Integer> set;
public static void main(String[] args) {
int sum=0;
for (int a= 1; a <=9 ; a++) {
for (int b = 1; b <=9 ; b++) {
for (int c = 1; c <=9; c++) {
for (int d = 1;d <=9 ; d++) {
for (int e =1; e <=9 ; e++) {
if(a!=b && a!=c && a!=d && a!=e && b!=c && b!=d && b!=e && c!=d && c!=e && d!=e){
String s=a+""+b;
String s1=c+""+d+""+e;
String x=a+""+d+""+b;
String x1=c+""+e;
int h=Integer.parseInt(s);
int h1=Integer.parseInt(s1);
int g=Integer.parseInt(x);
int g1=Integer.parseInt(x1);
if (h*h1==g*g1){
System.out.println(h +" "+ h1+" "+g+" "+g1 );
sum++;
}
}
}
}
}
}
}
System.out.println(sum);
}
}
Operation results:
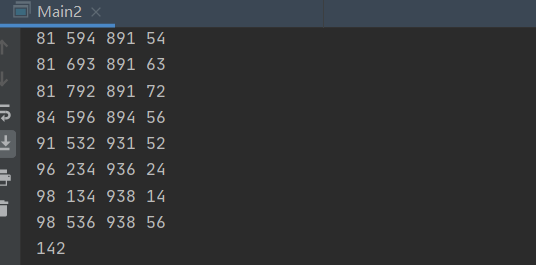
A total of 142 times
Question 3: Revitalizing China
Title Description
Xiao Ming took part in the interesting sports meeting of the school. One of the items is: grid jumping. There are some squares on the ground. Write a word in each square as follows: (see also p1.jpg)
Start with me
I started to revitalize
Start in revitalization
To revitalize China
During the competition, first stand in the grid with the word "from" in the upper left corner. You can jump horizontally or vertically to the adjacent grid, but you can't jump to the diagonal grid or other positions. Always jump to the end of the word "Hua". The route required to be skipped just constitutes the sentence "start with me and revitalize China".
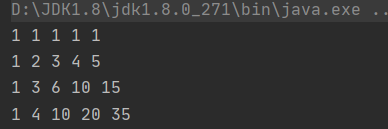
Please help Xiao Ming calculate how many possible jumping routes he has?

Code: (dynamic programming)
package java_b2013;
import java.util.Arrays;
public class Main3 {
public static void main(String[] args) {
//Define array
int [][]dp=new int[4][5];//ranks
//initialization
for (int i = 0; i < 4; i++) {
dp[i][0]=1;//Assign initial value to line
}
for (int i = 0; i < 5; i++) {
dp[0][i]=1;//Assign initial value to column
}
for (int i = 1; i < 4; i++) {
for (int j = 1; j < 5; j++) {
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 5; j++) {
System.out.print(dp[i][j]+" ");
}
System.out.println();
}
}
}
Operation results:
Question 4: Golden continued fraction
Title Description
The golden section number 0.61803... Is an irrational number. This constant is very important and will appear in many engineering problems. Sometimes you need to get this number very accurate. For some precision engineering, the accuracy of constants is very important. Perhaps you have heard of the Hubble Space Telescope. After its first launch, it found a manual processing error. For such a behemoth, in fact, it is only a mistake that the mirror is many times thinner than the hair, but it has become "myopia"!!
To get back to business, how do we get the golden section number as accurate as possible? There are many ways. The simpler one is to use continued fraction:
1
Gold number = ---------------------
1
1 + -----------------
1
1 + -------------
1
1 + ---------
1 + ...
code:
package java_b2013;
import java.math.BigDecimal;
import java.math.BigInteger;
public class Main4 {
public static void main(String[] args) {
BigInteger a = BigInteger.ONE;
BigInteger b = BigInteger.ONE;
//Fibonacci's iterative form
for (int i = 3; i < 500; i++) { //200 300 400 500
BigInteger t = b;
b = a.add(b); //Large integer addition
a = t;
}
//new BigDecimal(a, 110) converts an integer to BigDecimal, specifying an accuracy [length 110] / / division of large floating-point numbers
BigDecimal divide = new BigDecimal(a, 110).divide(new BigDecimal(b, 110), BigDecimal.ROUND_HALF_DOWN);
System.out.println(divide.toPlainString().substring(0, 103)); //[0, 102] 103 character string segmentation
//ROUND_HALF_DOWN: rounded; The usage of toplanstring() is similar to that of toString()
}
}
Operation results:
