Blue Bridge Cup - nine palaces rearrangement (python)
Title Description
as shown in the first figure below, in the nine palace grid, there are 1 ~ 8 digital cards, and another grid is empty. The cards in the grid adjacent to the empty grid can be moved to the space. After several moves, the situation shown in the second figure can be formed.
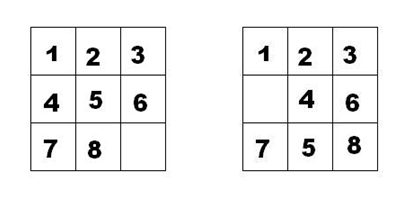
We record the situation of the first figure as: 12345678
Record the situation of the second figure as 123.46758
Obviously, the numbers are recorded from top to bottom and from left to right, and the spaces are recorded as periods.
The task of this topic is to know the initial and final states of the nine palaces and find out how many steps it can reach. If it cannot be reached no matter how many steps, output - 1.
input
The first line contains the initial state of the nine palaces, and the second line contains the final state of the nine palaces.
output
Output the minimum number of steps. If there is no scheme, output - 1.
sample input
12345678. 123.46758
sample output
3
Ideas and summary:
at first, dfs was adopted, but because the solution space of this problem is deep and it is easy to time out, bfs was replaced.
at the beginning of writing bfs, it still times out, so it is improved to convert the searched nodes into hash values and store them in the serached sequence. One example is passed, but there is still a time-out.
Go find the information C language network - Jiugong rearrangement problem solution.
by comparing the differences between your own code and its code, you can find the following points that can be used for reference in python Programming:
1. One dimensional arrays are mapped into two-dimensional arrays through coordinate transformation, which is faster than using two-dimensional arrays directly.
2. The searched nodes are stored in the dictionary in the form of key value pairs. Because the python dictionary is efficient, it is not necessary to traverse all key value pairs when checking whether the key is in the dictionary.
3. In the classification discussion, we can extract the changes in different cases, express them in an array, and traverse the array to write the same code for different cases, instead of directly moving up, down, left and right, and write the code once in each of the four cases.
4. By using divmod, the subscript of two-dimensional array represented by one-dimensional array is obtained.
5. Exchange a and b: A, b=b, a. The middle temp is omitted.
6,[element for row in temp for element in row]
Let's enjoy the big guy's code:
def bfs():
global start, end, cache_state
stack = [start]
while stack:
state = stack.pop(0)
for direction in around:
i, j = divmod(state.index('.'), 3)
if 0 <= i + direction[0] < 3 and 0 <= j + direction[1] < 3:
# temp = [list(state[3 * k:3 * k + 3]) for k in range(3)]
# temp[i][j], temp[i + direction[0]][j + direction[1]] = temp[i + direction[0]][j + direction[1]], temp[i][j]
# temp = ''.join(element for row in temp for element in row)
temp = list(state)
idx_0, idx_1 = 3 * i + j, 3 * (i + direction[0]) + j + direction[1]
temp[idx_0], temp[idx_1] = temp[idx_1], temp[idx_0]
temp = ''.join(temp)
if temp not in cache_state:
cache_state.setdefault(temp, cache_state[state] + 1)
stack.append(temp)
if temp == end:
return cache_state[end]
start, end = [input().strip() for _ in range(2)]
cache_state, around = {start: 0}, [[-1, 0], [0, -1], [1, 0], [0, 1]]
print(bfs())
Sorry to post my own code:
##while True:
s = input()
ls1 = list(s)
s = input()
ls2 = list(s)
queue = list()
# initialization
i, j = divmod(ls1.index("."), 3)
dot = [i,j]
steps = 0
searched = {"".join(ls1):None}
queue.append([ls1[:], dot[:], steps])
while len(queue)!=0:
ls1, dot, steps = queue.pop(0)
if ls1 != ls2 and steps < 81:
# turn left
if dot[1] != 0:
# Generate nodes and join the queue
ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]-1]=ls1[dot[0]*3+dot[1]-1], ls1[dot[0]*3+dot[1]]
dot[1] -= 1
temp = "".join(ls1)
if temp not in searched:
searched[temp] = None
queue.append([ls1[:], dot[:], steps+1])
ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]+1]=ls1[dot[0]*3+dot[1]+1], ls1[dot[0]*3+dot[1]]
dot[1] += 1
# turn right
if dot[1] != 2:
# Generate nodes and join the queue
ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]+1]=ls1[dot[0]*3+dot[1]+1], ls1[dot[0]*3+dot[1]]
dot[1] += 1
temp = "".join(ls1)
if temp not in searched:
searched[temp] = None
queue.append([ls1[:], dot[:], steps+1])
ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]-1]=ls1[dot[0]*3+dot[1]-1], ls1[dot[0]*3+dot[1]]
dot[1] -= 1
# Go up
if dot[0] != 0:
# Generate nodes and join the queue
ls1[dot[0]*3+dot[1]], ls1[(dot[0]-1)*3+dot[1]]=ls1[(dot[0]-1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
dot[0] -= 1
temp = "".join(ls1)
if temp not in searched:
searched[temp] = None
queue.append([ls1[:], dot[:], steps+1])
ls1[dot[0]*3+dot[1]], ls1[(dot[0]+1)*3+dot[1]]=ls1[(dot[0]+1)*3+dot[1]], ls1[dot[0]*3+ dot[1]]
dot[0] += 1
# Go down
if dot[0] != 2:
# Generate nodes and join the queue
ls1[dot[0]*3+dot[1]], ls1[(dot[0]+1)*3+dot[1]]=ls1[(dot[0]+1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
dot[0] += 1
temp = "".join(ls1)
if temp not in searched:
searched[temp] = None
queue.append([ls1[:], dot[:], steps+1])
ls1[dot[0]*3+dot[1]], ls1[(dot[0]-1)*3+dot[1]]=ls1[(dot[0]-1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
dot[0] -= 1
else:
break
if steps == 81:
print(-1)
else:
print(steps)
the improved program has no problem running on the C language network, but there are two timeouts on the Blue Bridge Cup official website. I hope someone with talent can point out the maze.
Reference link:
C language network - Jiugong rearrangement problem solution