Write in front

Friends, we meet again ~ this article has been delayed again and again, and finally finished. This article talks about several true topics of investigating DFS and BFS in the Blue Bridge Cup. You can take a look at the previous two articles, which are very detailed about search. [10000 words] preparation for Blue Bridge Cup algorithm competition (I) -- search topic (I) (C + +) as well as Preparation for Blue Bridge Cup algorithm competition (I) -- search topic (II) (C + +) .

Well, no more nonsense. Enter today's study~

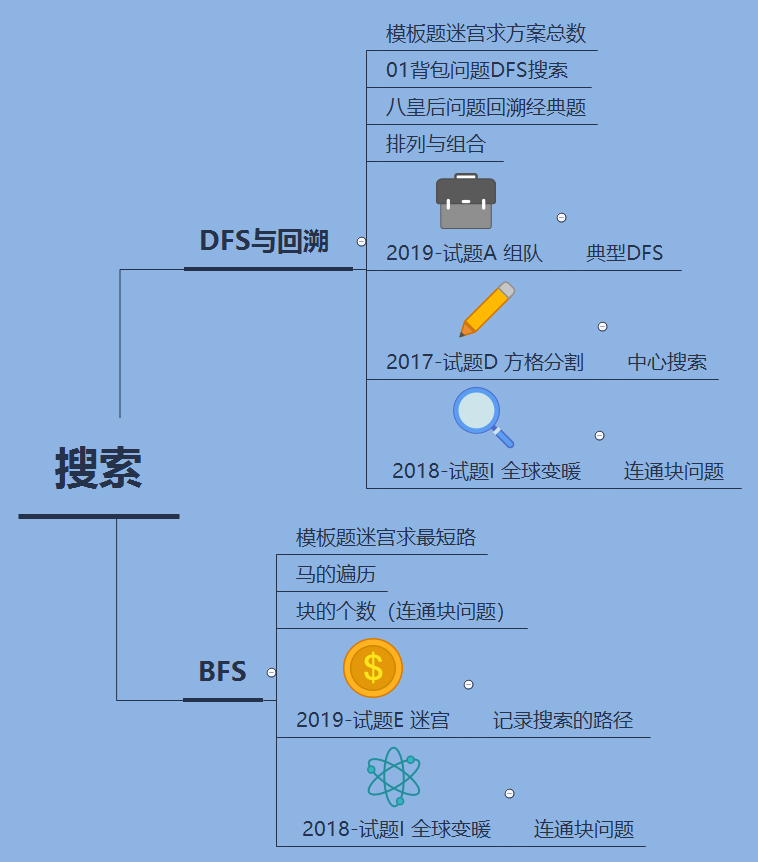
1, Summary of search ideas

This is Luogu's summary of DFS and BFS search. It is precisely because of the characteristics of these two search algorithms that they are more efficient than violent enumeration. They can deal with problems with small data scale. Some large data scale need pruning optimization or find other efficient algorithms.

DFS	BFS
Total number of suitable schemes	It is suitable for solving the shortest path and connectivity problems
Using recursion	Using queue 1
Exploratory search	Carpet search
Go down a road to the black	Always w try the state closest to the initial state first

You can do the questions according to the list I wrote. Oh ~ see if you have mastered DFS and BFS.

2, Blue Bridge Cup (search algorithm)

1. 2017 test question D grid segmentation

Title Link

Topic analysis
First of all, we have to consider the problem of how to make the shape of the two parts cut exactly the same.
These two parts must be about centrosymmetry. If such a rule is found, the idea of this problem will be clear.

Starting from the center point (3,3), we conduct DFS search in four directions: up, down, left and right. When we reach the boundary, it indicates that a segmentation scheme is formed. Then go back to find the next segmentation scheme. Of course, there are some details to pay attention to.

• When a point (x, y) is searched, its centrosymmetric point (6 - x, 6 - y) cannot be searched. Therefore, two marks are required, i.e. [1] [maze - 6]. (indicates that the point has been visited)

Why is the symmetry point (6 - x, 6 - y)? Let's draw the following picture and have a look~

• Since the topic says that rotational symmetry belongs to the same cutting method, a segmentation scheme rotates clockwise around the center point to obtain the same scheme as the original scheme. So we divide the ans after DFS by 4.

AC code

//2017 split grid
#include <iostream>
#include <cstring>
using namespace std;

int maze[7][7];//Represents the point of the grid, maze[x][y] = 1 indicates that the point has been accessed
int dx[4] = {0, -1, 1, 0};
int dy[4] = {-1, 0, 0, 1};//Offset
int ans;

void dfs(int x, int y)
{
    if (x == 0 || x == 6 || y == 0 || y == 6)//Reach boundary ans+1   
    {
        ans++;
        return;
    }
    for (int i = 0; i < 4; i++)//Search in four directions
    {
        int x1 = x + dx[i];
        int y1 = y + dy[i];
        if (maze[x1][y1] != 1)//Not accessed
        {
            maze[x1][y1] = 1;
            maze[6 - x1][6 - y1] = 1;//Set the point and its symmetry point as accessed
            dfs(x1, y1);
            maze[x1][y1] = 0;
            maze[6 - x1][6 - y1] = 0;//Go back and restore the scene
        }
    }
}

int main()
{
    maze[3][3] = 1;//At the beginning, set the center point as accessed.
    dfs(3, 3);
    cout << ans / 4 << endl;//Rotational symmetry belongs to the same segmentation scheme
    return 0;
}

2. 2019 test question group A

Title Link


Topic analysis
This question is a blank filling question. What is the maximum possible sum of scores? Because the amount of data in this question is small, we can calculate it by hand.

In addition, this question is a typical DFS problem. For position 1, it has 20 choices, while for position 2, it has 19 choices except for the player selected in position 1, and so on. Then the idea of DFS is very clear. We start DFS from position 1 and maintain the index currently being selected and the sum of the current scores. When the DFS of positions 1 ~ 5 is completed, maxsum is used to update the maximum sum of scores.
To sum up, there are two solutions to this problem:

• DFS search (accurate)
• Observation + manual calculation (fastest)

Answer 1. DFS

#include <iostream>
using namespace std;

int maxsum;
int maze[20][5];
bool visited[20];

void dfs(int index, int sum)
{
    if (index == 5)//Position 5 has been processed
    {
        maxsum = max(maxsum, sum);//Update the sum of maximum scores
        return;
    }

    for (int i = 0; i < 20; i++)
    {
        if (maze[i][index] != 0 && visited[i]== false)
        {
            visited[i] = true;
            dfs(index + 1, sum + maze[i][index]);
            visited[i] = false;
        }
    }
}

int main()
{
    for (int i = 0; i < 20; i++)
    {
        for (int j = 0; j < 5; j++)
        {
            cin >> maze[i][j];
        }
    }
    dfs(0, 0);
    cout << maxsum;
    return 0;
    //maxsum = 490
}

Answer 2. Observation + manual calculation

It is easy to find out the maximum sum of scores, which will not be discussed in detail here.

3. 2018 - question I global warming

Title Link


Topic analysis

• How to judge whether a piece of land is submerged? If there are four directions of land up, down, left and right, then the land will not be submerged, otherwise it will be submerged.
• Number of islands completely submerged = number of islands before inundation ans1 - number of islands after inundation ans2.
• Find an island through DFS search and mark its land to prevent repeated search. And find land that is not submerged, ans2 + +.

The idea of this problem is not too difficult. You can see the notes of the code for specific details~

AC code

#include <iostream>
using namespace std;

const int N = 1010;
char maze[N][N];
int ans1, ans2;
bool flag;
int n;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};

bool check(int x, int y)
{
    if (maze[x][y] == '.') return false;
    if (x < 0 || x >= n || y < 0 || y >= n) return false;
    return true;
}
void dfs(int x, int y)
{
    // if (maze[x][y] != '#') return;
    int ans = 0;
    if (!flag)//No land was found to meet the conditions
    {        
        for (int i = 0; i < 4; i++)//The purpose is to find out if there are four lands around
        {
            int x1 = x + dx[i];
            int y1 = y + dy[i];
            if (check(x1, y1))
            {
                ans++;
            }
        }
    }
    if (ans == 4)
    {
        ans2++;
        flag = true;//Find the land that meets the conditions, and set the flag to true
    }
    maze[x][y] = '*';//Set the visited land to * to prevent repeated visits
    for (int i = 0; i < 4; i++)
    {
        int x1 = x + dx[i];
        int y1 = y + dy[i];
        if (check(x1, y1) && maze[x1][y1] != '*')
        {
            dfs(x1, y1);
        }
    }

}//One dfs can find a connecting block, that is, an island

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> maze[i];
    }

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (maze[i][j] == '#'/ / search only when it is land
            {
                ans1++;//dfs gets several islands several times
                dfs(i, j);
                flag = false;//Remember to restore the flag after DFS completes an island
            }
        }
    }
    cout << ans1 - ans2 << endl;
    return 0; 
}

Of course, this problem can also be realized by BFS. Small partners can do it to deepen their understanding of DFS and BFS.

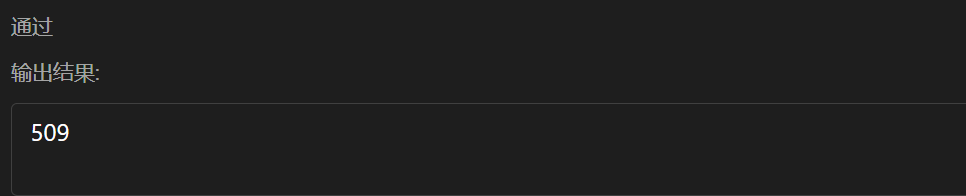
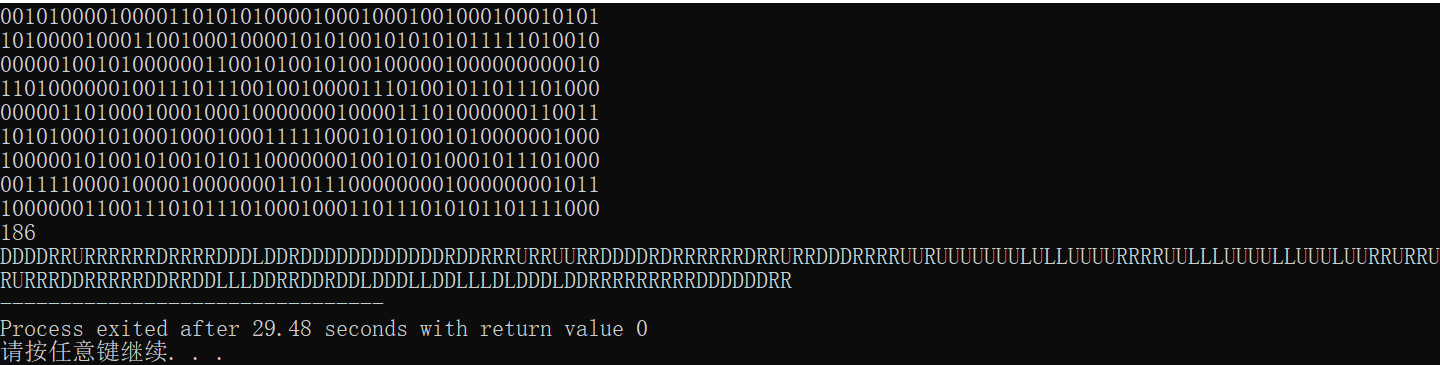
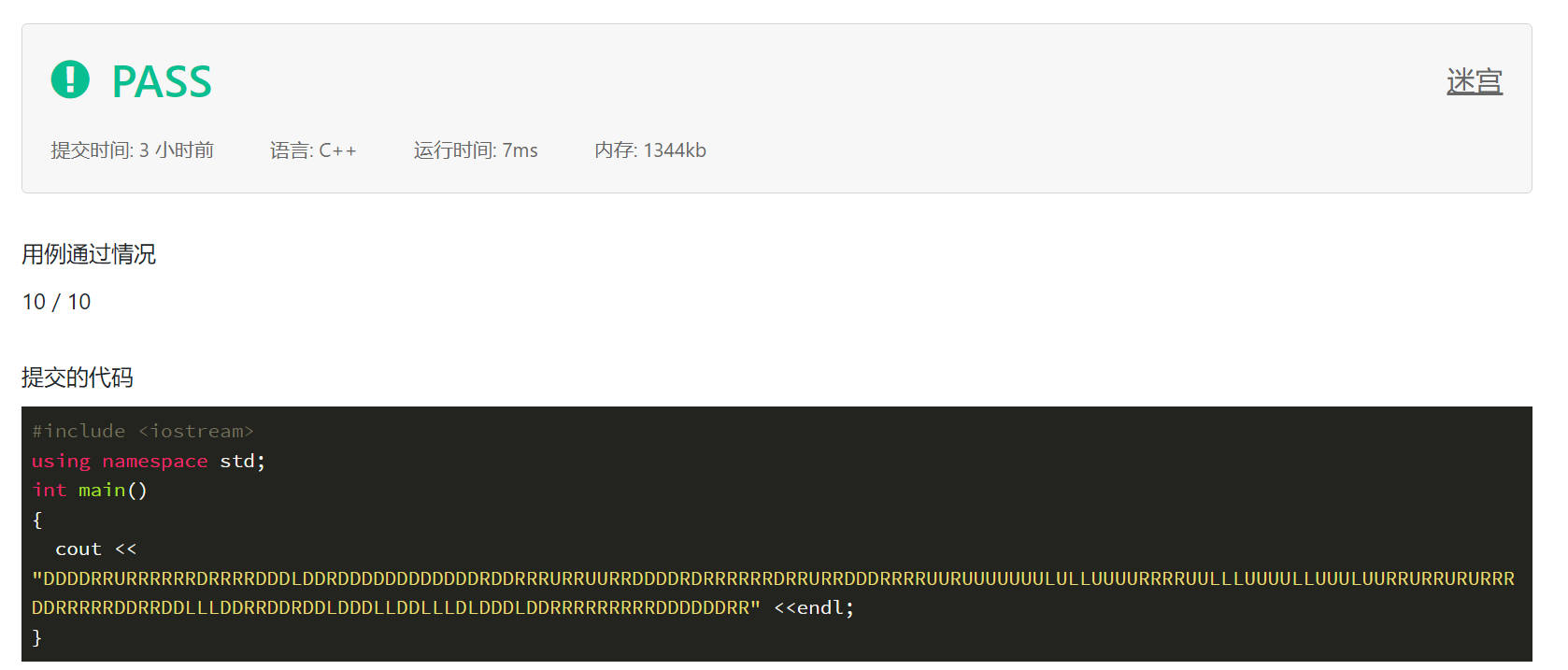
4. 2019 test question E maze

Title Link


Topic analysis
This question is similar to Preparation for Blue Bridge Cup algorithm competition (I) -- search topic (II) (C + +) The shortest path problem in the maze is similar, but this problem also needs to record the search path and output the path with the smallest dictionary order.

How to ensure that the output is the path with the smallest dictionary order? We only need to search according to the order of DLRU in the search process, and the final shortest path must be the path with the smallest dictionary order. To do this, we need to set the direction array.

• int dx[4] = {1, 0, 0, -1};
• int dy[4] = {0, -1, 1, 0};

(1,0) means going down, (0, - 1) means going left, (0,1) means going right and (- 1,0) means going up. EH ~ wait a minute, the thinking partners should have found something wrong. There is something wrong with the direction array. It is clear that (- 1,0) is going down. How can it be up? I'm sorry for these people. Come on. Don't panic. I'll draw a picture for you.

After looking at this picture, my friends should understand that we can't use the traditional direction array to represent this problem. This is a pit of this problem. To be honest, I got stuck here at the beginning.

Set a structure, which stores the coordinates and steps of the point and records the path to the point.

struct node
{
    int x;
    int y;
    int step;
    string ans;
}

In the process of search, record the path to the point. We can set a DIC array to represent DLRU. When a point is queued, node ans = temp. ans + dic[i];.

Then set the template directly in other places~

AC code

#include <iostream>
#include <queue>
#include <string>

using namespace std;
//DLRU
// int dx[4] = {0, -1, 1, 0};
// int dy[4] = {-1, 0, 0, 1};
int dx[4] = {1, 0, 0, -1};
int dy[4] = {0, -1, 1, 0};
bool inq[55][55];
char maze[55][55];
char dic[4] = {'D', 'L', 'R', 'U'};

struct node
{
    int x;
    int y;
    int step;
    string ans;
}s, t, Node;

bool check(int x, int y)
{
    if (x < 0 || x >= 30 || y < 0 || y >= 50) return false;
    if (inq[x][y]) return false; 
    if (maze[x][y] == '1') return false;
    return true;
}

void bfs()
{
    queue<node> q;
    q.push(s);
    inq[s.x][s.y] = true;
    while (!q.empty())
    {
        node temp = q.front();
        q.pop();
        if (temp.x == t.x && temp.y == t.y)
        {
            cout << temp.step << endl << temp.ans;
            return;
        }
        for (int i = 0; i < 4; i++)
        {
            int x1 = temp.x + dx[i];
            int y1 = temp.y + dy[i];
            if (check(x1, y1))
            {
                Node.x = x1;
                Node.y = y1;//I began to forget to assign values to X and y of Node, and I couldn't get results.
                Node.step = temp.step + 1;
                Node.ans = temp.ans + dic[i];
                q.push(Node);
                inq[x1][y1] = true;
            }
        } 
    }
}

int main()
{
    for (int i = 0; i < 30; i++)
    {
        
        for (int j = 0; j < 50; j++)
        {
           maze[i][j] = getchar();

        }
        getchar();//Consumption and carriage return
    }
    s.x = 0, s.y = 0, s.step = 0, s.ans = "";
    t.x = 29, t.y = 49;
    bfs();
    return 0;
}
//186
//DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRD//DDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDD//LLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

Write it at the back

The explanation of search will come to an end. Next, I will write several articles on dynamic planning. Last year, my friends also found that the Blue Bridge Cup has strengthened the examination of DP thought, and DP is also the focus of our preparation as well as search. Little friends can look forward to it. The next article will be finished in three days

It's not easy to create. Let's pay attention to it with one key and three times~