In this paper, Java language is used to describe the data structure and algorithm, which can be used in work and interviews. That is to sum up the common data structure, and the corresponding implementation methods in Java, in order to sum up the theory and practice step by step.
Common Data Structures
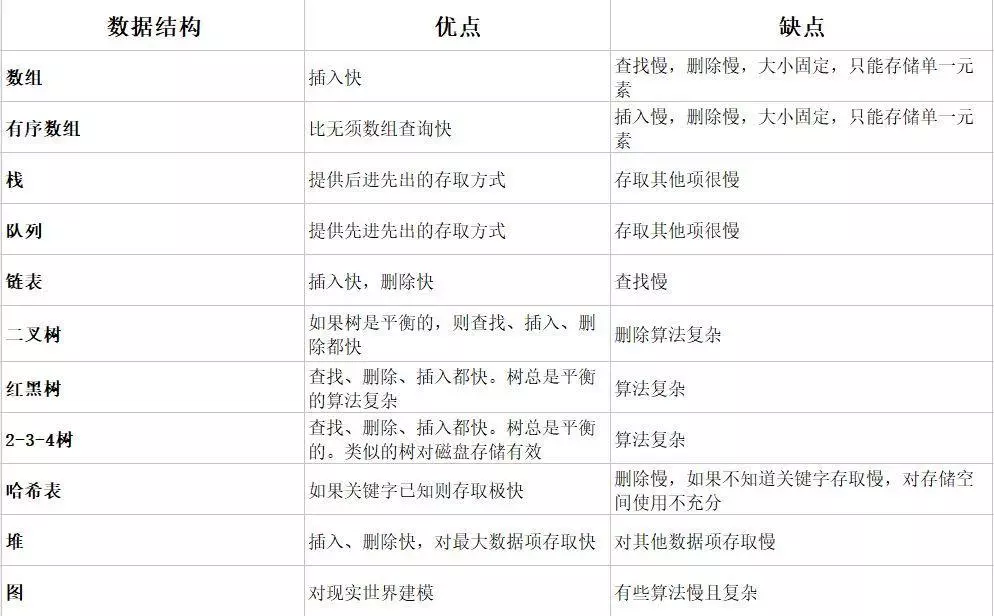
array
An array is a set of elements of the same data type arranged in a certain order, and it is a continuous memory space. The advantage of arrays is that both get and set operation times are O(1); the disadvantage is that both add and remove operation times are O(N).
In Java, Array is an array. In addition, Array List uses Array as its implementation basis. Compared with general Array, the biggest advantage of Array List is that we don't need to consider crossing the boundaries when adding elements. When elements exceed the array capacity, it automatically expands the guaranteed capacity.
The main difference between Vector and Array List is that there is one more thread security, but the efficiency is lower. Today, the java.util.concurrent package provides many thread-safe collection classes (such as LinkedBlockingQueue), so you don't need to use Vector anymore.
int[] ints = new int[10]; ints[0] = 5;//set int a = ints[2];//get int len = ints.length;//Array length
linked list
Link list is a discontinuous and non-sequential structure. The logical order of data elements is realized by the order of pointer links in the list, which consists of a series of nodes. The advantage of linked list is that both add and remove operation time are O(1); the disadvantage is that both get and set operation time are O(N), and additional space is needed to store items pointing to other data addresses.
The lookup operation is O(N) for unsorted arrays and linked list times.
In Java, LinkedList uses linked lists as its basic implementation.
LinkedList<String> linkedList = new LinkedList<>();
linkedList.add("addd");//add
linkedList.set(0,"s");//set, you must first ensure that the linkedList already has the 0th element
String s = linkedList.get(0);//get
linkedList.contains("s");//lookup
linkedList.remove("s");//deletequeue
Queue is a special linear table. It only allows deletion at the front end of the table, and insertion at the back end of the table, which is called FIFO.
In Java, LinkedList implements Deque, which can be used as a two-way queue (or, naturally, a one-way queue). In addition, PriorityQueue implements a priority queue, that is, each element of the queue has priority, and the elements are sorted according to priority.
Deque<Integer> integerDeque = new LinkedList<>(); //The difference between entering the team at the end is that if it fails //The add method throws an IllegalStateException exception, and the offer method returns false integerDeque.offer(122); integerDeque.add(122); //The difference is if you fail. //The remove method throws a NoSuchElementException exception, and the poll method returns false int head = integerDeque.poll();//Returns the first element and deletes it from the queue head = integerDeque.remove();//Returns the first element and deletes it from the queue //The difference is if you fail. // The element method throws a NoSuchElementException exception, and the peek method returns null. head = integerDeque.peek();//Return the first element without deleting it head = integerDeque.element();//Return the first element without deleting it
Stack
Stack, also known as stack, is a linear table with limited operations. The limitation is that insertion and deletion operations are allowed only at one end of the table. This end is called the top of the stack, and the other end is called the bottom of the stack. It embodies the characteristics of LIFO.
In Java, Stack implements this feature, but Stack also inherits Vector, so it has two features: thread safety line and inefficiency. In the latest JDK8, Deque is recommended to implement stack, such as:
Deque<Integer> stack = new ArrayDeque<Integer>(); stack.push(12);//Tail stacking stack.push(16);//Tail stacking int tail = stack.pop();//Tail out of the stack and delete the element tail = stack.peek();//Tail out of stack, do not delete this element
aggregate
Collection refers to the collection of concrete or abstract objects with a specific nature. These objects are called the elements of the set. Their main characteristic is that the elements are not repeatable.
In Java, HashSet embodies this data structure, and HashSet is built on the basis of MashMap. LinkedHashSet inherits HashSet, uses HashCode to determine the location in the collection, and uses linked list to determine the location, so there is order. TreeSet implements the SortedSet interface, which is an ordered set (built on top of TreeMap), so the lookup operation is faster (log(N)) than the normal Hashset; the insertion operation is slower (log(N)) because the order is maintained.
HashSet<Integer> integerHashSet = new HashSet<>(); integerHashSet.add(12121);//Add to integerHashSet.contains(121);//Does it include integerHashSet.size();//Collection size integerHashSet.isEmpty();//Is it empty?
Hash table
Hash table, also known as hash table, is a data structure accessed according to key value. It accesses records by mapping key code values to a location in the table to speed up the search. This mapping function is called hash function.
HashMap implements hash table in Java, and Hashtable has one more thread security than it does, but its performance is low due to the use of global locks, so now Concurrent HashMap is generally used to implement thread-safe HashMap (similarly, the above data structures are almost right in the latest java.util.concurrent package). The corresponding high-performance thread-safe classes. TreeMap implements the SortMap interface, which can sort the records it saves by keys. LinkedHashMap retains the order in which elements are inserted.
WeakHashMap is an improved HashMap, which implements a "weak reference" to the key. If a key is no longer referenced externally, the key can be reclaimed by GC without the need for us to delete it manually.
HashMap<Integer,String> hashMap = new HashMap<>(); hashMap.put(1,"asdsa");//Add to hashMap.get(1);//Get hashMap.size();//Number of elements
tree
A tree is a finite set of n (n > 0) nodes, in which:
-
Each element is called a node.
-
There is a specific node called the root node or tree root.
-
The other data elements except the root node are divided into m (m > 0) disjoint combinations T1, T2,... Tm-1, in which each set Ti (1<=i<=m) is itself a tree, called subtree of the original tree.
Trees are widely used in the computer world, such as red and black trees in operating systems, B + trees in databases, grammar trees in compilers, heaps in memory management (essentially trees), Huffman coding in information theory, and so on. TreeSet and TreeMap use trees to arrange in Java. Orders (Binary Search improves retrieval speed), but programmers usually need to define a tree class and implement related properties, without an API.
Now we use Java to implement various common trees.
Binary Tree
Binary tree is a basic and important data structure. Each node has at most two subtrees. Binary tree has left and right subtrees. At the first level, there are at most 2^(i-1) nodes (i starts from 1); and at most 2 ^ (k) - 1 nodes for a binary tree whose depth is K. For any binary tree, if its terminal node is n0, the degree is 2. If the node number is n2, then n0=n2+1.
The properties of binary trees:
-
In the non-empty binary tree, the total number of nodes in the first layer does not exceed 2 ^ (i-1), I >= 1;
-
The binary tree with depth h has at most 2^h-1 nodes (h > = 1) and at least h nodes.
-
For any binary tree, if the number of leaf nodes is N0 and the total number of nodes with degree 2 is N2, then N0=N2+1;
-
The depth of a complete binary tree with n nodes is log2(n+1).
-
If the nodes of a complete binary tree with N nodes are stored sequentially, the relationships between them are as follows: if I is the node number, then if I > 1, the parent node number is I/2; if 2I <= N, the left son (i.e., the root node of the left subtree) number is 2I; if 2I > N, there is no left son; if 2I+1 <= N, then the father node number is I/2; if 2I > N, there is no left son; and if 2I+1 <= N, there is no left son. The node number of his right son is 2I+1; if 2I+1 > N, there is no right son.
-
Given N nodes, different binary trees of h(N) can be constructed, in which h(N) is the N-th term of the Cattleland number and h(n)=C(2*n, n)/(n+1).
-
There are I branches, I is the sum of the road lengths of all branches, J is the sum of the road lengths of leaves J=I+2i.
Full Binary Tree and Complete Binary Tree
Full binary tree: Except that there are no sub-nodes in the last layer, all nodes on each layer have two sub-nodes.
Complete binary tree: If the depth of the binary tree is h, the number of nodes in all other layers (1 to (h-1) reaches the maximum, and all nodes in the H layer are continuously concentrated on the left side, which is the complete binary tree.
Full binary tree is a special case of complete binary tree.
Binary search tree
Binary search tree, also known as Binary Sort Tree or Binary Search Tree. A binary sorting tree is either an empty tree or a binary tree with the following properties:
-
If the left subtree is not empty, the value of all nodes in the left subtree is less than that of its root node.
-
If the right subtree is not empty, the value of all nodes in the right subtree is greater than or equal to the value of its root node.
-
The left and right subtrees are also binary sort trees.
-
There are no nodes with equal keys.
The nature of binary search tree: If the binary search tree is traversed in middle order, an ordered sequence can be obtained. The time complexity of binary search tree: It is the same as binary search. The time complexity of insertion and search is O(logn), but in the worst case there will still be O(n) time complexity. The reason is that the tree is not balanced when inserting and deleting elements. What we are pursuing is that in the worst case there is still a better time complexity, which is the original intention of balanced binary tree design.
Binary lookup trees can be expressed as follows:
public class BST<Key extends Comparable<Key>, Value> {
private Node root; //Root node
private class Node {
private Key key; //Sorting interval
private Value val; //Corresponding values
private Node left, right; //Left subtree, right subtree
private int size; //The tree rooted on this node contains the number of nodes
public Node(Key key, Value val, int size) {
this.key = key;
this.val = val;
this.size = size;
}
}
public BST() {}
public int size() {//Get the number of nodes in the binary tree
return size(root);
}
private int size(Node x) {Get the number of tree containing nodes rooted on this node
if (x == null) return 0;
else return x.size;
}
}Find:
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {//Find key in tree rooted by x node
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) return get(x.left, key);//Recursive left subtree lookup
else if (cmp > 0) return get(x.right, key);//Recursive right subtree search
else return x.val;//Eureka
}Insert:
public void put(Key key, Value val) {
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {In order to x Search in trees with roots at nodes key,val
if (x == null) return new Node(key, val, 1);
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = put(x.left, key, val);//Recursive left subtree insertion
else if (cmp > 0) x.right = put(x.right, key, val);//Recursive right subtree insertion
else x.val = val;
x.size = 1 + size(x.left) + size(x.right);
return x;
}Delete:)
public Key min() {
return min(root).key;
}
private Node min(Node x) {
if (x.left == null) return x;
else return min(x.left);
}
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node x) {//Delete the minimum subtree with x as the root node
if (x.left == null) return x.right;
x.left = deleteMin(x.left);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = delete(x.left, key);//Remove left subtree recursively
else if (cmp > 0) x.right = delete(x.right, key);//Remove right subtree recursively
else { //This node is the node to be deleted.
if (x.right == null) return x.left;//Without the right subtree, hang the left subtree on the parent node of the original node
if (x.left == null) return x.right;//There is no left subtree. Hang the right subtree on the parent node of the original node.
Node t = x;//Replacing the deleted node with the smallest node in the right subtree still guarantees the orderliness of the tree.
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.size = size(x.left) + size(x.right) + 1;
return x;
} balanced binary tree
Balanced binary tree, also known as AVL tree, has the following properties: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and the left and right subtrees are both a balanced binary tree. Its appearance is to solve the problem that the unbalanced binary search tree leads to the degradation of the search efficiency to a linear one, because the balance of the tree is maintained when deleting and inserting, so that the search time is kept at O(logn), which is more stable than the binary search tree.
The ode of ALLTree is composed of the ode of BST plus the private int height; the Node height attribute can be used to judge whether the tree is balanced or not.
The key to maintaining tree balance is rotation. For a balanced node, since there are at most two sons at any node, it is easy to see that the height difference between the two subtrees of this node is 2 when the height is unbalanced. This unbalance occurs in the following four cases:
-
The height of the left subtree 3 nodes of 6 nodes is 2 larger than that of the right subtree 7 nodes, and the height of the left subtree 1 node of the left subtree 3 nodes is larger than that of the right subtree 4 nodes, which becomes the left left left subtree.
-
The height of the left subtree 2 nodes of 6 nodes is 2 larger than that of the right subtree 7 nodes, and the height of the left subtree 1 node of the left subtree 2 nodes is less than that of the right subtree 4 nodes.
-
The left subtree 1 node height of 2 nodes is 2 smaller than the right subtree 5 nodes, and the left subtree 3 node height of the right subtree 5 nodes is higher than the right subtree 6 nodes, which becomes the right left.
-
The left subtree 1 node height of 2 nodes is 2 less than the right subtree 4 nodes, and the left subtree 3 node height of the right subtree 4 nodes is less than the right subtree 6 nodes, which becomes the right right subtree.
As can be seen from Figure 2, 1 and 4 are symmetrical. The rotation algorithms in these two cases are identical. It only needs one rotation to achieve the goal. We call them single rotation. Two and three cases are also symmetrical, and the rotation algorithms in these two cases are the same, requiring two rotations, which we call double rotation.
Single rotation is directed at the left and right situations, which are symmetrical. As long as the left and left situations are solved, the right and right situations will work well. Figure 3 is the solution for left-left case. Node k2 does not satisfy the balance characteristic, because its left subtree K1 is two layers deeper than the right subtree Z, and the deeper one in the K1 subtree is the left subtree X subtree of k1, so it belongs to the left-left case.
In order to restore the balance of the tree, we turn K1 into the root node of the tree. Because K2 is larger than k1, K2 is placed on the right subtree of k1, whereas Y is larger than K1 and smaller than K2 in the right subtree of k1, we put Y on the left subtree of k2, which not only satisfies the nature of the binary search tree, but also satisfies the nature of the balanced binary tree.
This operation only needs a part of the pointer change. As a result, we get another binary search tree, which is an AVL tree, because X moves up one layer, Y stays on the original level, Z moves down one layer. The new height of the whole tree is the same as that of the left subtree which was not inserted before. The insertion operation makes the X height longer. Therefore, since the height of the subtree remains unchanged, the path to the root node does not need to continue to rotate. Code:
private int height(Node t){
return t == null ? -1 : t.height;
}
//Left left circumstance single rotation
private Node rotateWithLeftChild(Node k2){
Node k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k1.size = k2.size;
k2.size = size(k2.right)+size(k2.left)+1;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1; //Return to the new root.
}
//Right-right single rotation
private Node rotateWithRightChild(Node k2){
Node k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
k1.size = k2.size;
k2.size = size(k2.right)+size(k2.left)+1;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.right), k2.height) + 1;
return k1; //Return to the new root.
} Double rotation is aimed at both right and left cases. Single rotation can not make it reach a balanced state. It has to go through two rotations. Similarly, the two situations are symmetrical. As long as the situation of right and left is solved, the right and left will be easy to handle. Fig. 4 is the solution of left-right situation. The node k3 does not satisfy the balance characteristic, because its left subtree K1 is two layers deeper than the right subtree Z, and the deeper one in the K1 subtree is the right subtree k2 subtree of k1, so it belongs to left-right situation.
In order to restore the balance of the tree, we need to do two steps. The first step is to take k1 as the root and rotate right and right once. After rotation, it becomes left and left. So the second step is to rotate left and left again. Finally, we get a balanced binary tree with k2 as the root. Code:
//Left and right situation
private Node doubleWithLeftChild(Node k3){
try{
k3.left = rotateWithRightChild(k3.left);
}catch(NullPointerException e){
System.out.println("k.left.right For:"+k3.left.right);
throw e;
}
return rotateWithLeftChild(k3);
}
//Right-left situation
private Node doubleWithRightChild(Node k3){
try{
k3.right = rotateWithLeftChild(k3.right);
}catch(NullPointerException e){
System.out.println("k.right.left For:"+k3.right.left);
throw e;
}
return rotateWithRightChild(k3);
} AVL lookup operation is the same as BST. The deletion and insertion operations of AVL need to check whether the balance is balanced on the basis of BST. If the balance is not balanced, the rotation operation should be used to maintain the balance.
private Node balance(Node x) {
if (balanceFactor(x) < -1) {//Right high
if (balanceFactor(x.right) > 0) {//Right left
x.right = rotateWithLeftChild(x.right);
}
x = rotateWithRightChild(x);
}
else if (balanceFactor(x) > 1) {//Left high
if (balanceFactor(x.left) < 0) {//About
x.left = rotateWithRightChild(x.left);
}
x = rotateWithLeftChild(x);
}
return x;
}
private int balanceFactor(Node x) {
return height(x.left) - height(x.right);
}heap
The heap is a complete binary tree. In this tree, all parent nodes satisfy the heap of larger than or equal to their child nodes, and all parent nodes satisfy the heap of smaller than or equal to their child nodes. Although the heap is a tree, it is usually stored in an array. The parent-child relationship between the parent and child nodes is determined by array subscripts. The following small root heap and the array that stores it:
Values: 7, 8, 9, 12, 13, 11
Array Index: 0, 1, 2, 3, 4, 5
How to calculate the index of its parent node and left and right child nodes by an index of a node in an array?
public int left(int i) {
return (i + 1) * 2 - 1;
}
public int right(int i) {
return (i + 1) * 2;
}
public int parent(int i) {
//i is the root node
if (i == 0) {
return -1;
}
return (i - 1) / 2;
}Maintain the nature of the big pile:
public void heapify(T[] a, int i, int heapLength) {
int l = left(i);
int r = right(i);
int largest = -1;
//Find the root node and its left and right sub-nodes, the maximum of the three elements
if (l < heapLength && a[i].compareTo(a[l]) < 0) {
largest = l;
} else {
largest = i;
}
if (r < heapLength && a[largest].compareTo(a[r]) < 0) {
largest = r;
}
//If the element at i is not the largest, the element at i is exchanged with the element at the maximum, so that the element at i becomes the largest.
if (i != largest) {
T temp = a[i];
a[i] = a[largest];
a[largest] = temp;
//After exchanging elements, the tree rooted by a[i] may not satisfy the large root heap property, so the method is called recursively.
heapify(a, largest, heapLength);
}
}Tectonic Reactor:
public void buildHeap(T[] a, int heapLength) {
//Looking back and forth, the element at the lengthParent is the first element with child nodes, so starting with it, the heap is maintained.
int lengthParent = parent(heapLength - 1);
for(int i = lengthParent; i >= 0; i--){
heapify(a, i, heapLength);
}
}Use of heap: heap sorting, priority queue. In addition, because the adjustment cost is small, it is also suitable for real-time type sorting and change.