This paper is a collection of notes after learning the basic sorting algorithm, which is not entirely original. Personal learning ability is limited. The pictures are made by myself. There may be errors in words and pictures. If found, I hope to point out.
Since some leaders have conducted in-depth analysis of various algorithms, this blog is only to record, sort out and share my notes and process of self-study algorithms. I hope to communicate with algorithm learners. Please watch the officials.

Bubble sorting

Compare the size of two adjacent numbers from one end of the sequence, and exchange the positions of the two numbers according to the results. In this process, the data is like a bubble, floating from one end to the other.

The following is an illustration:





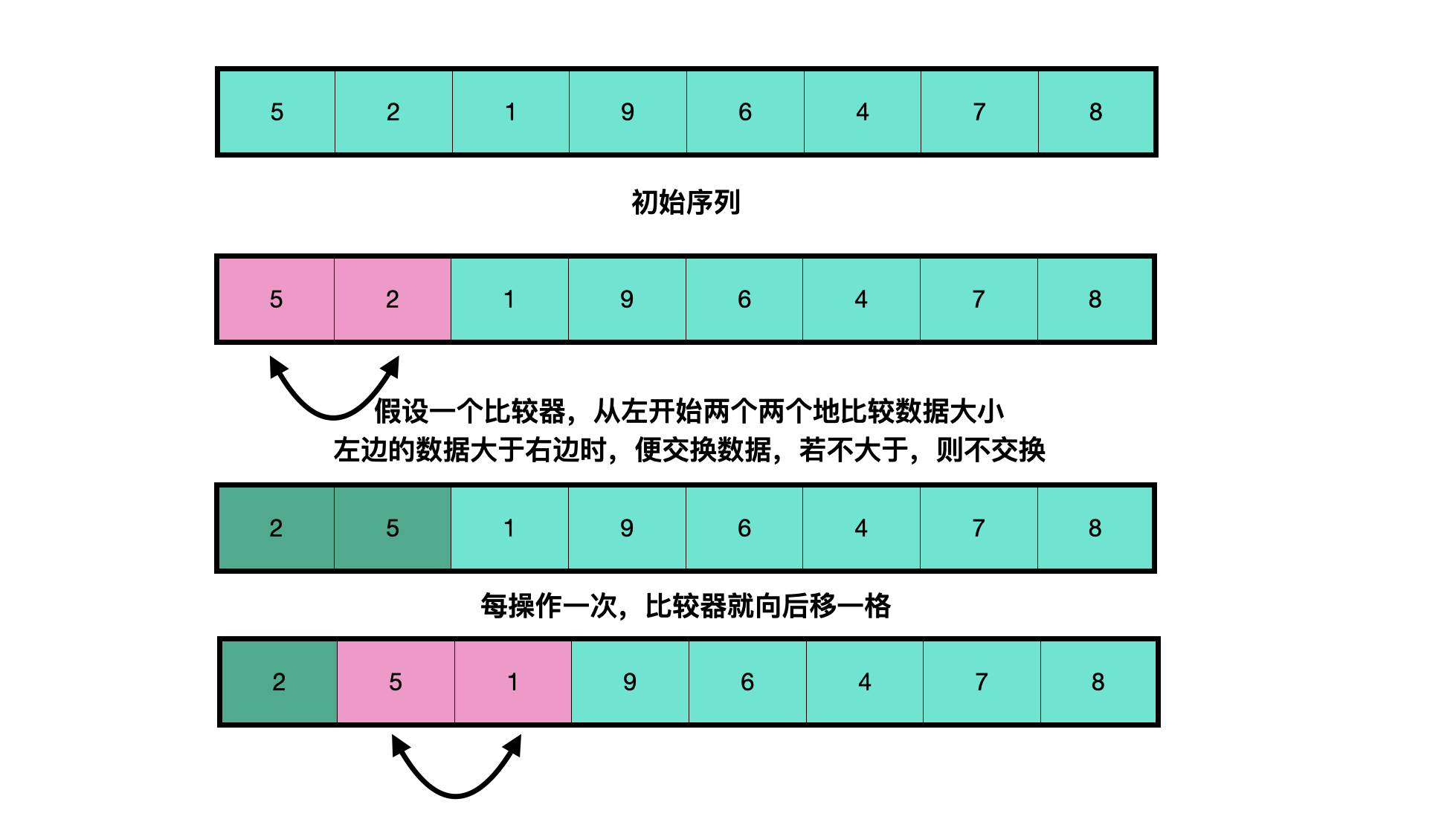
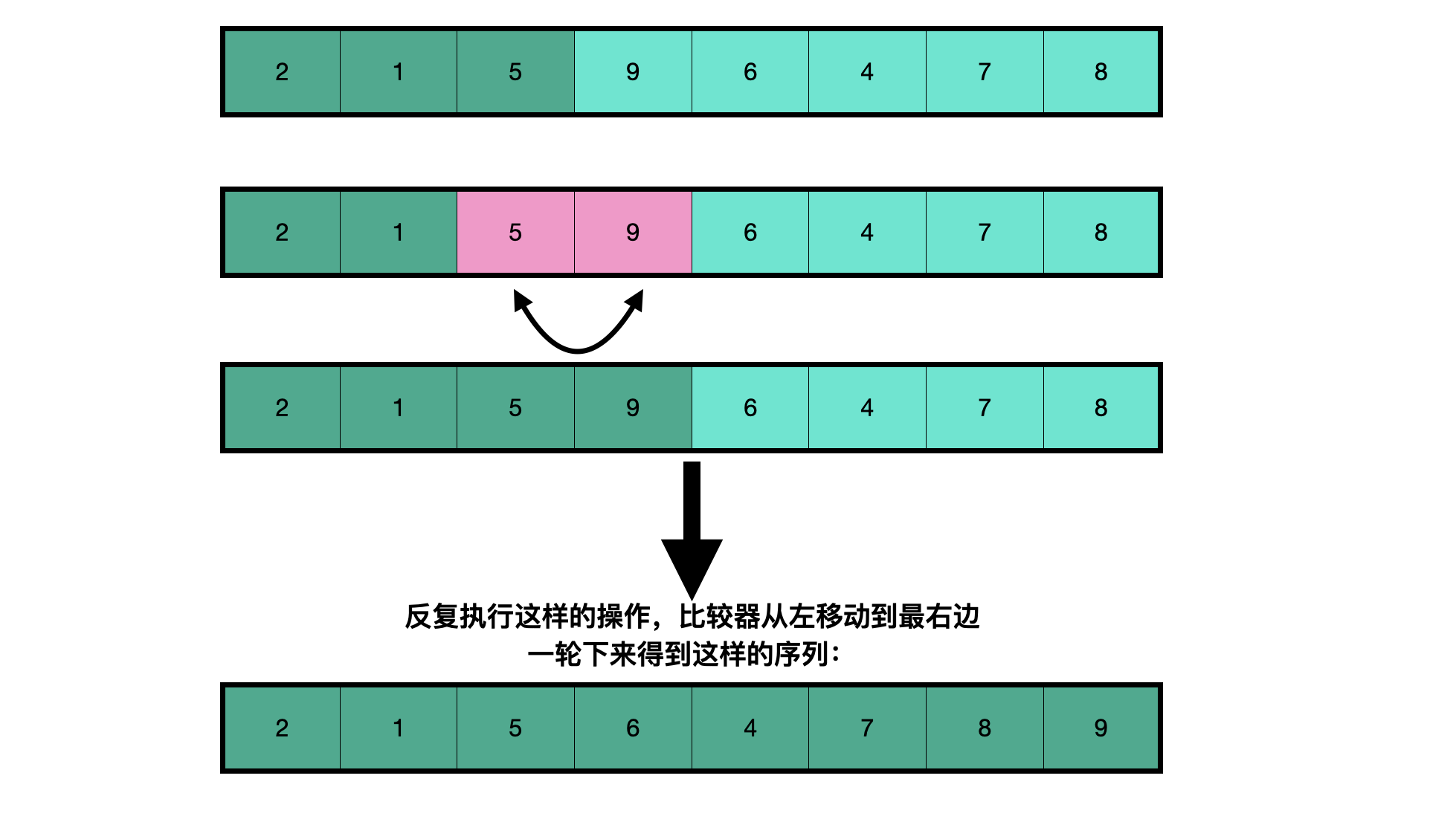
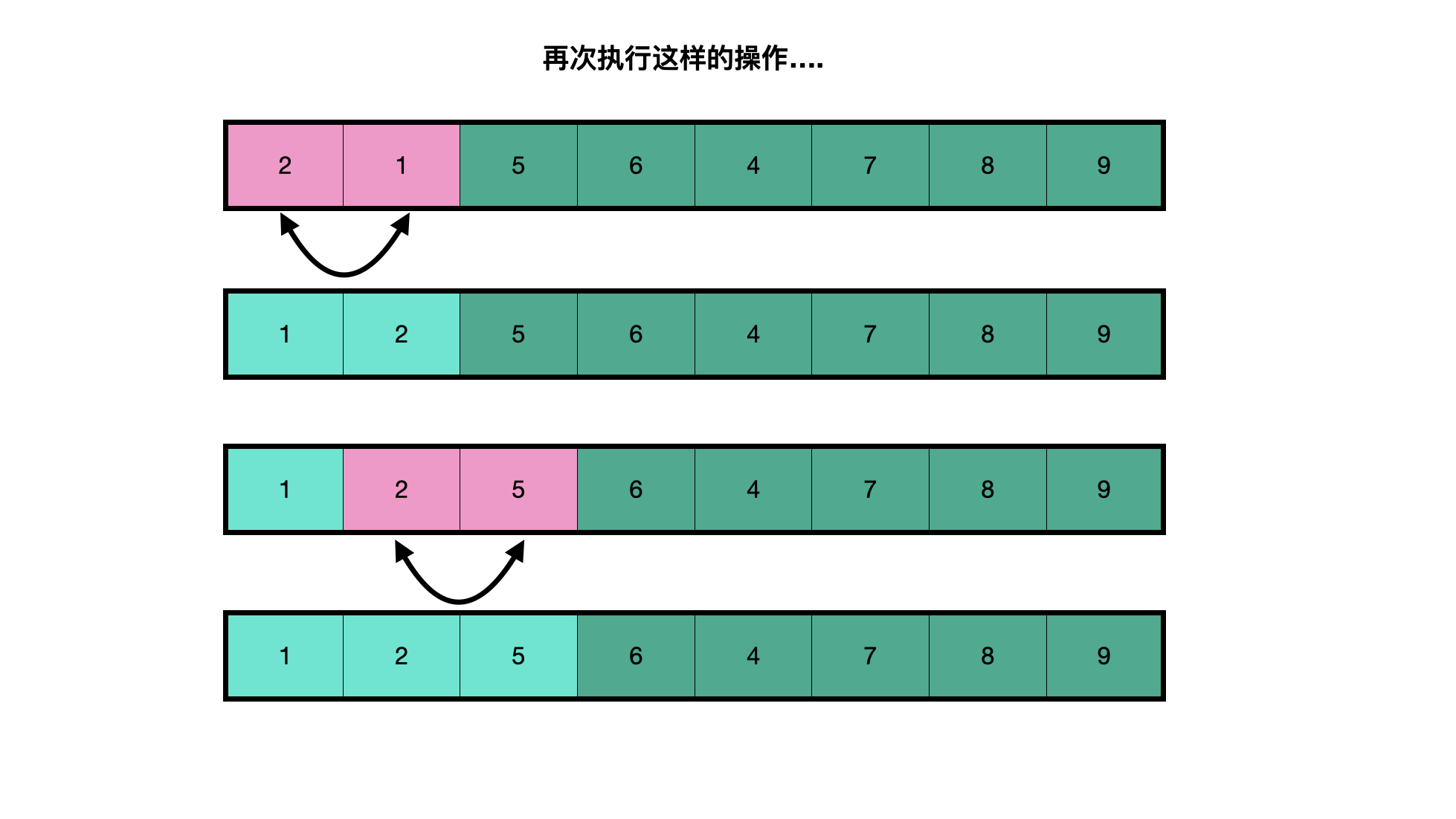
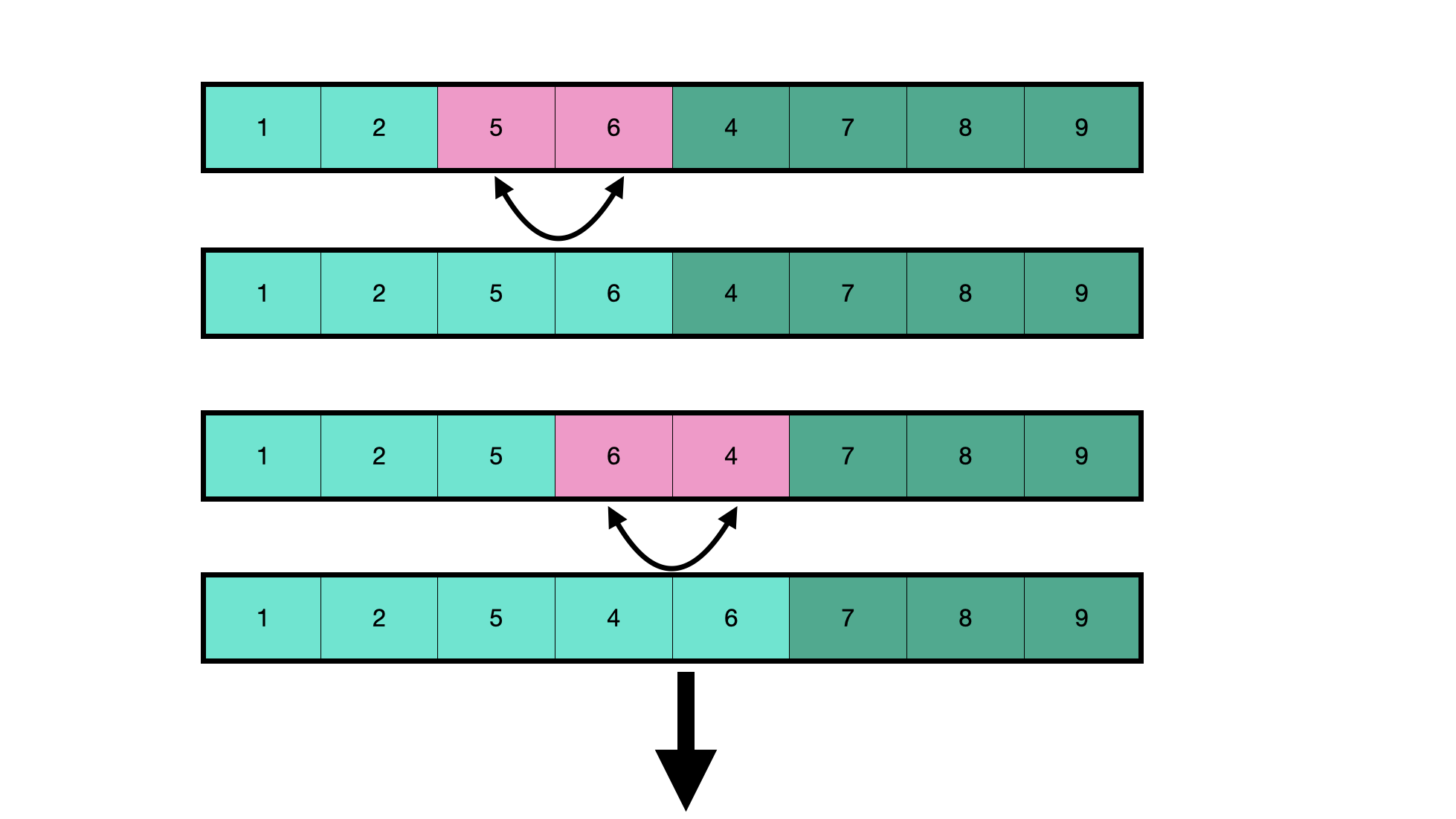
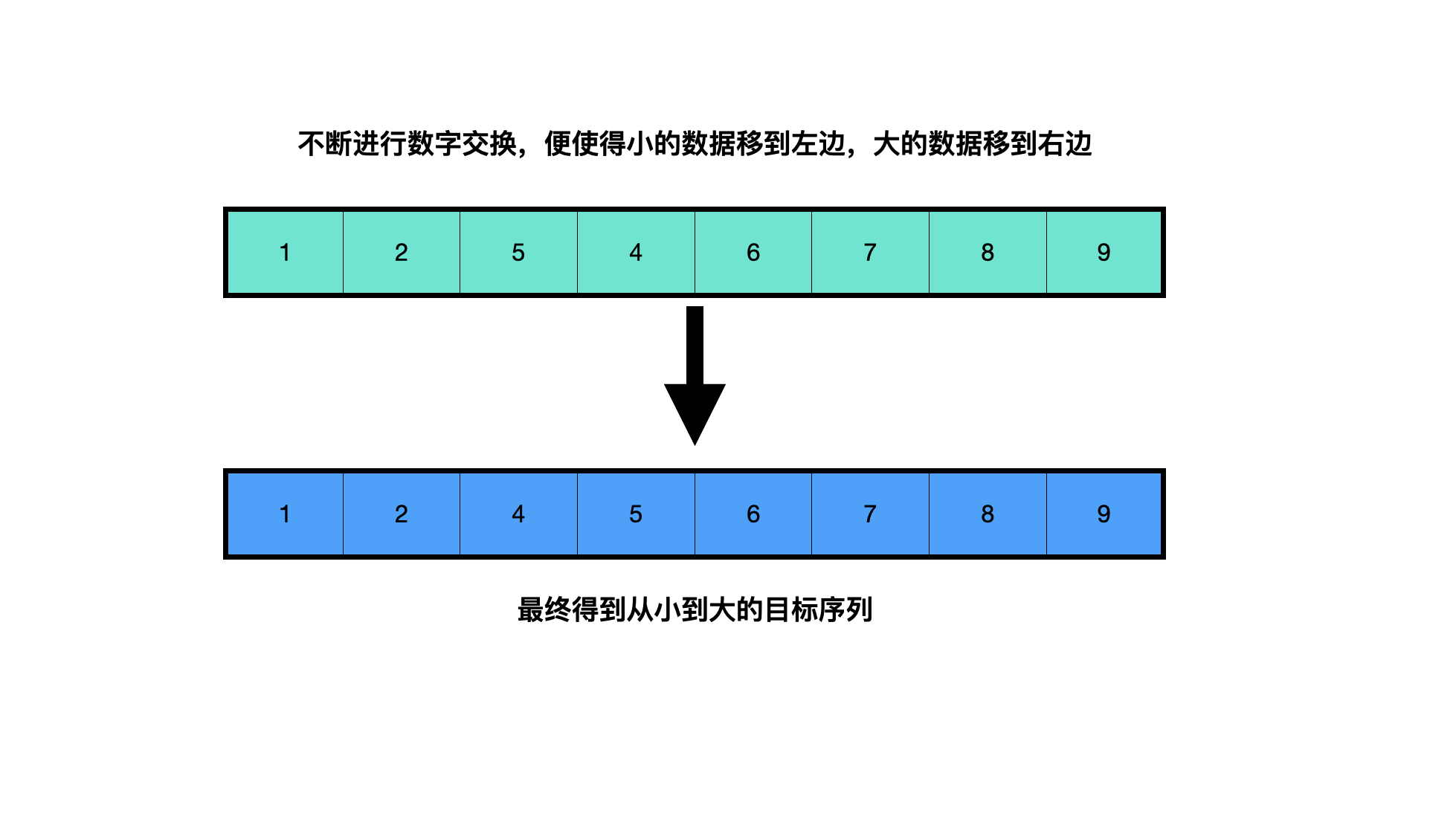
In the process of learning, the thought is easy to understand. You can write the following code:

public class BubbleSort {
        public static void BubbleSort (int []A) {
        for (int i = 0; i < A.length; i++) {
            for (int j = 0; j < A.length - 1; j++) {
                if (A[j+1] < A[j]) {
                    Swap.swap(A,j,j+1);
                }
            }
        }
    }
}

The definition of Swap is:

public class Swap {
    public static void swap(int[] A,int i,int t){
        int temp=0;
        temp=A[i];
        A[i]=A[t];
        A[t]=temp;
    }
}

If the number of data is n, it can be seen that the first round needs to be compared n-1 times, the second round needs to be compared n-2 times... The N-1 round needs to be compared once. Therefore, the total number of comparisons is (n - 1) + (n - 2) +... + 1 ≈ n2/2. The comparison times are fixed and independent of the arrangement order of the input data. The number of exchanges is related to the arrangement order of the input data. In extreme thought, if the input data is just arranged in the target order, there is no need for any exchange. On the contrary, data exchange is required for each comparison. Therefore, the time complexity is O(n2).

Find sort

Find the minimum value linearly from the data to be sorted (when sorting from small to large, find the maximum value from large to small), exchange its position with the leftmost data position in the unordered data, and the data after exchange is regarded as sorted.

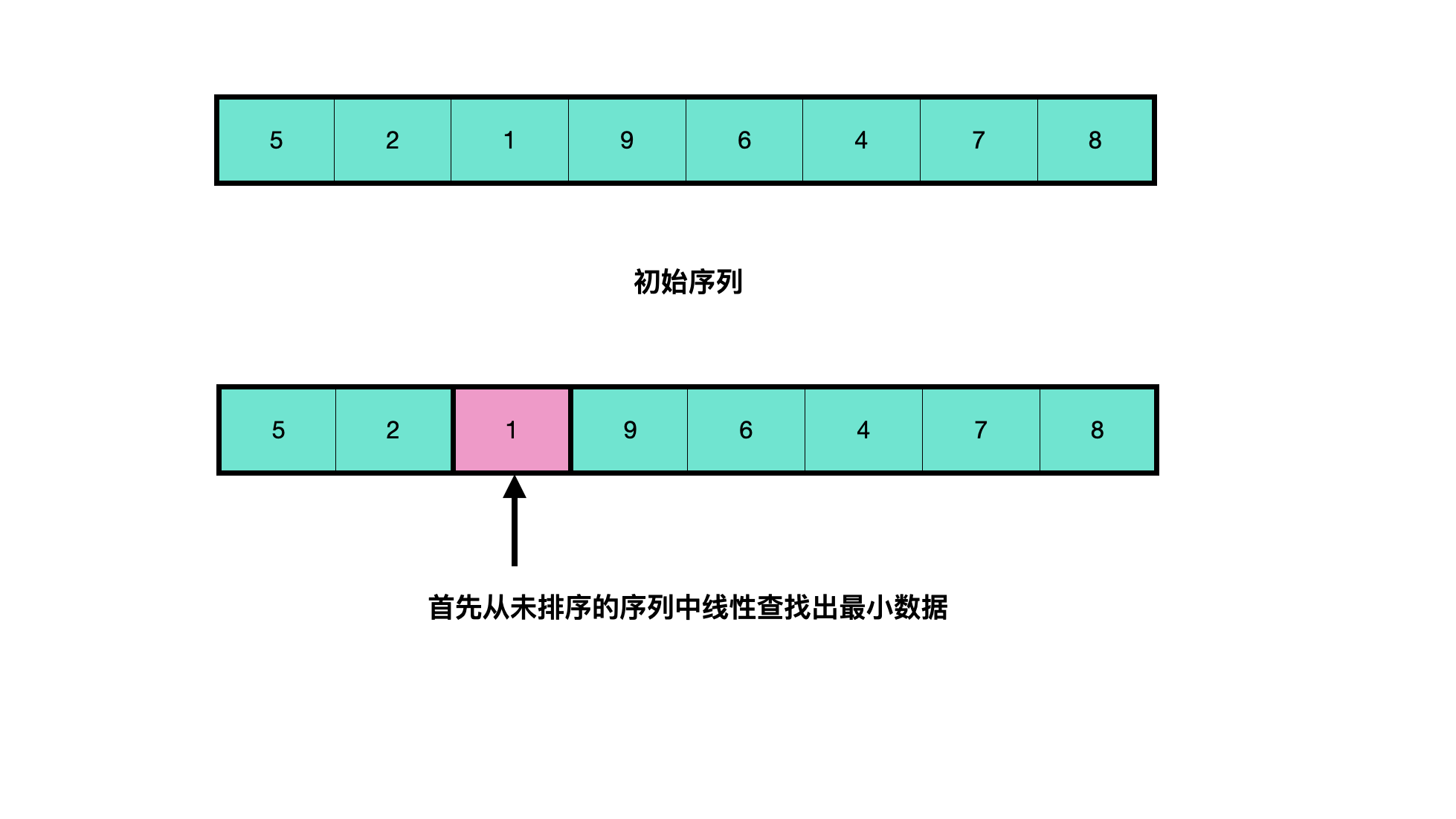
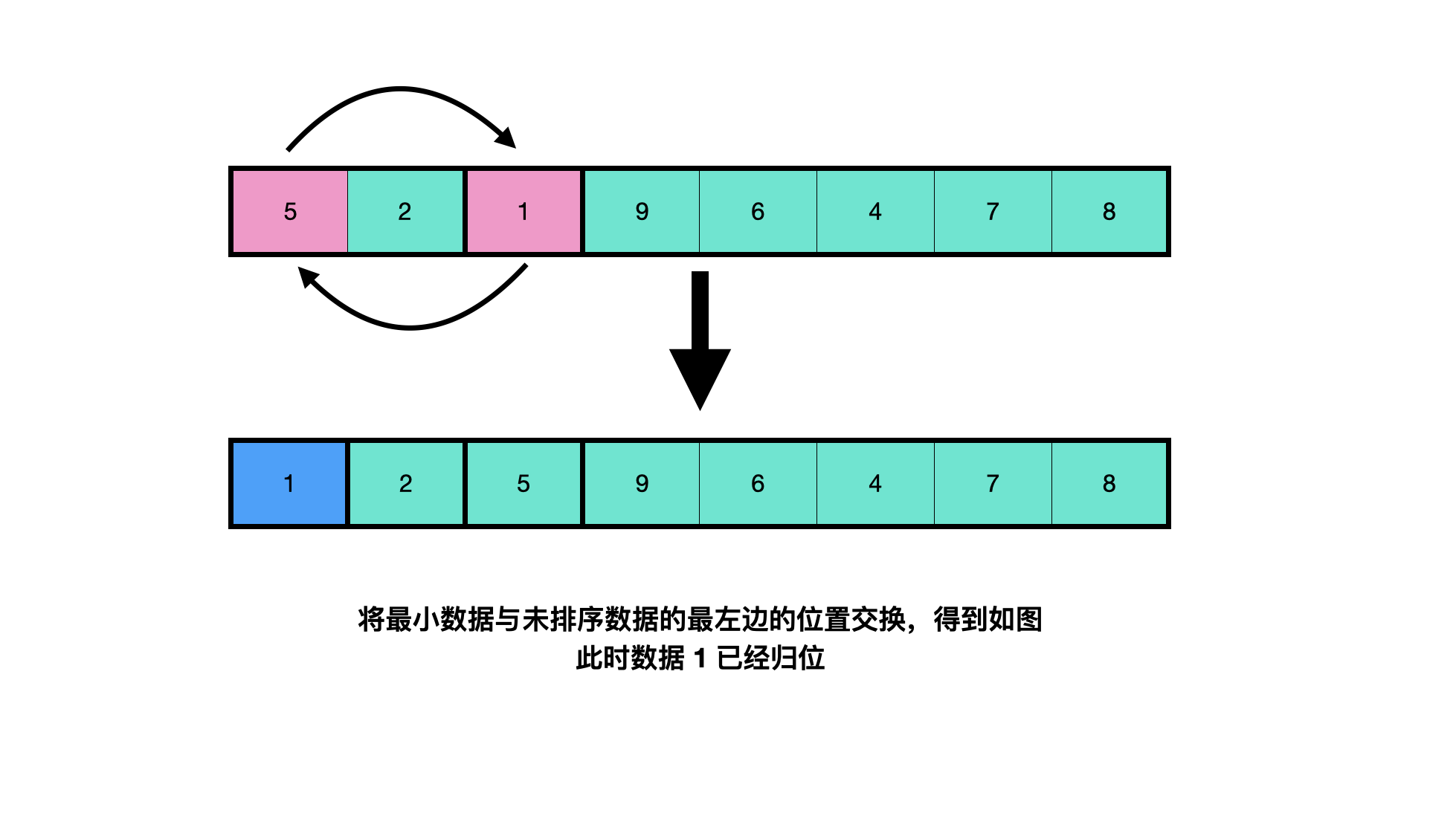
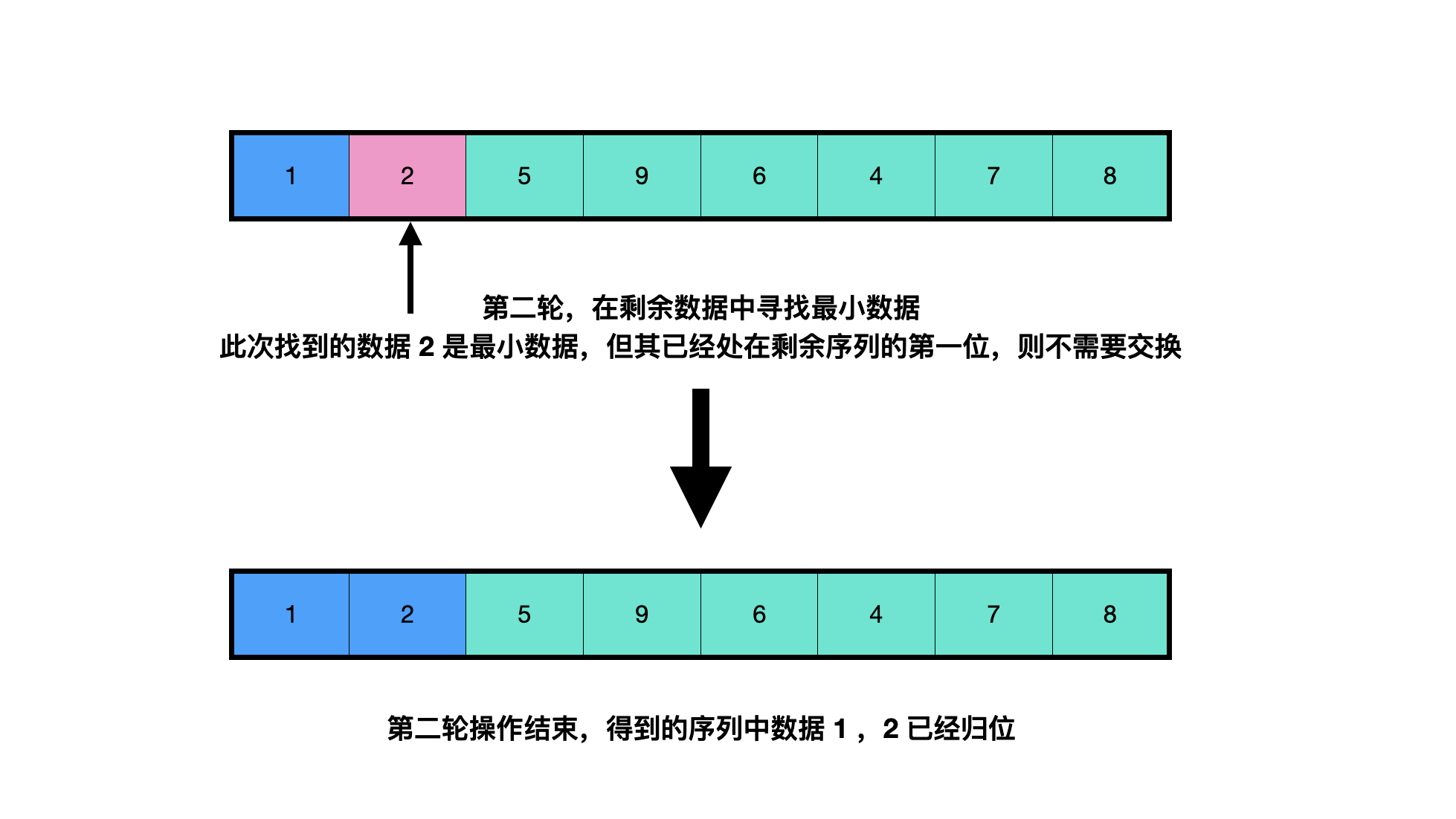
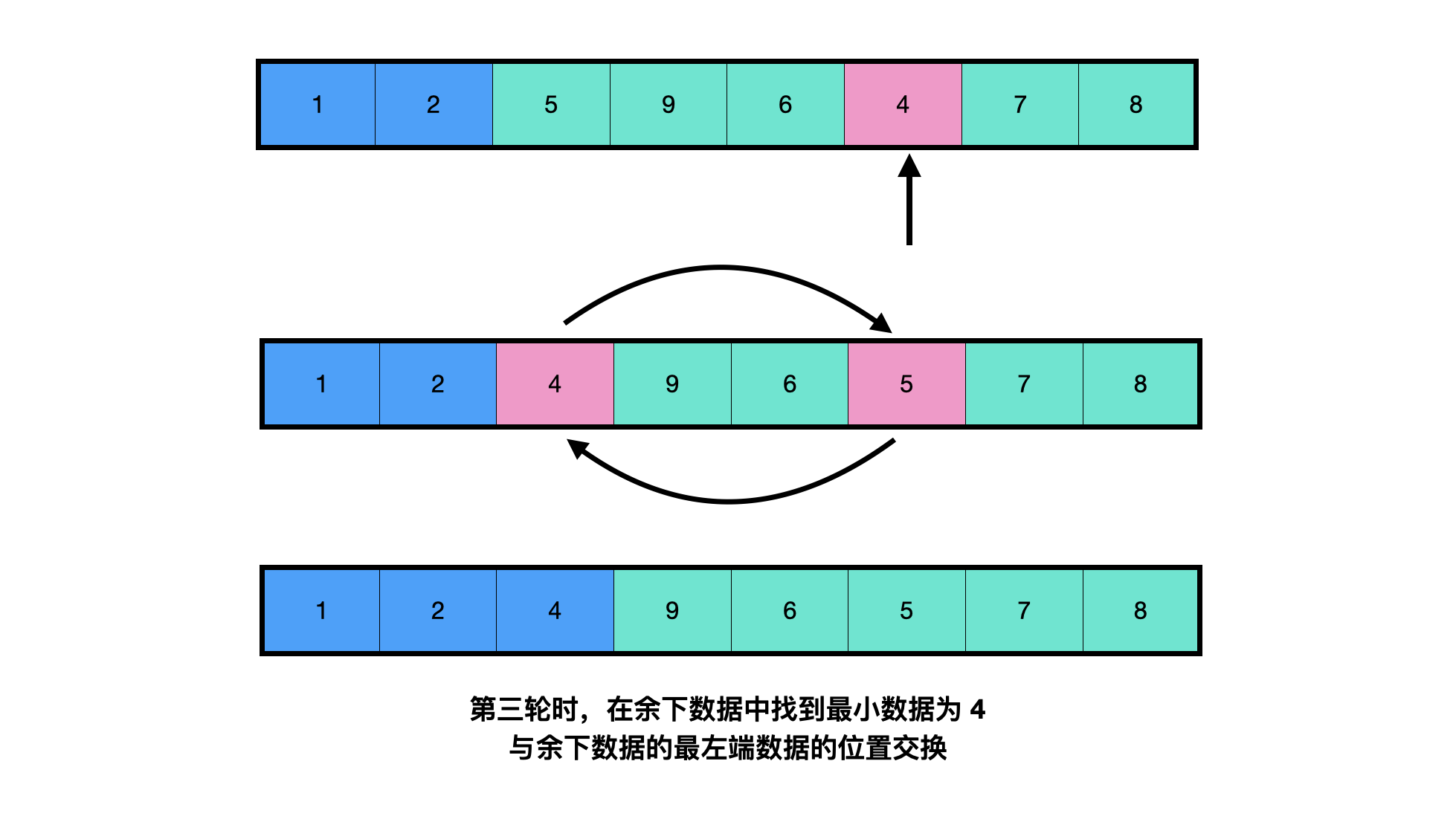
The code is as follows (from small to large):

public class SelectionSort {
    public static void selection(int[] A){
        int key=0, temp=0;
        for(int I=0;i<A.length-1;i++){
            key=i;  //Record the first position of unordered data, and start from here to find the minimum value
            for (int j=i+1;j<A.length;j++){
                if(A[key]>A[j]){		//Find minimum
                    key=j;			//Record the subscript of the minimum value in key
                }
            }
            if(i!=key)
			Swap.swap(A, i, key);	//If the key value changes, the data position is exchanged, and swap refers to the definition in bubble
        }
    }
}

Select sorting and use linear search. You need to compare (n-1)+(n-2) +... + 1 ≈ n2/2 times. The number of exchanges is related to the input data. If the input data is just in the target order, it does not need to be exchanged. On the contrary, it needs to be exchanged at most n-1 times. The complexity is O(n2).

Insert sort

Insertion sorting (taking sorting from small to large as an example) is an algorithm for comparing and sorting data from left. When sorting, the array can be regarded as the left (returned part) and the right (not returned part). Start with the first data on the left of the non homing part, compare it with the data of the homing part on the left. If it is less than, exchange the position with it, continue to compare to the left, and if it is greater than, end the comparison.

Simply put, it is to take out the data from the unordered (not returned) part in turn, and find a suitable position for it to insert in the returned part.

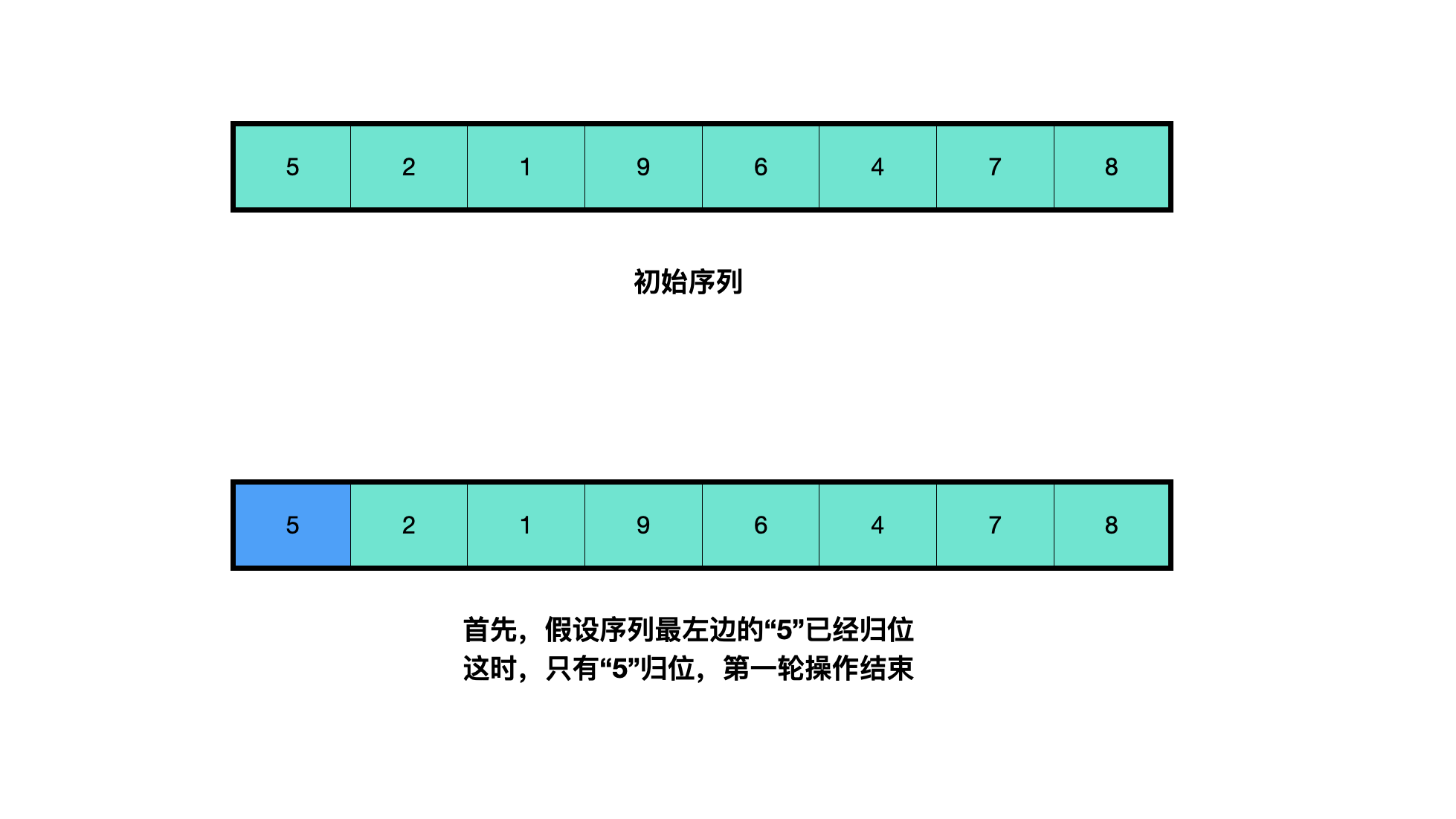
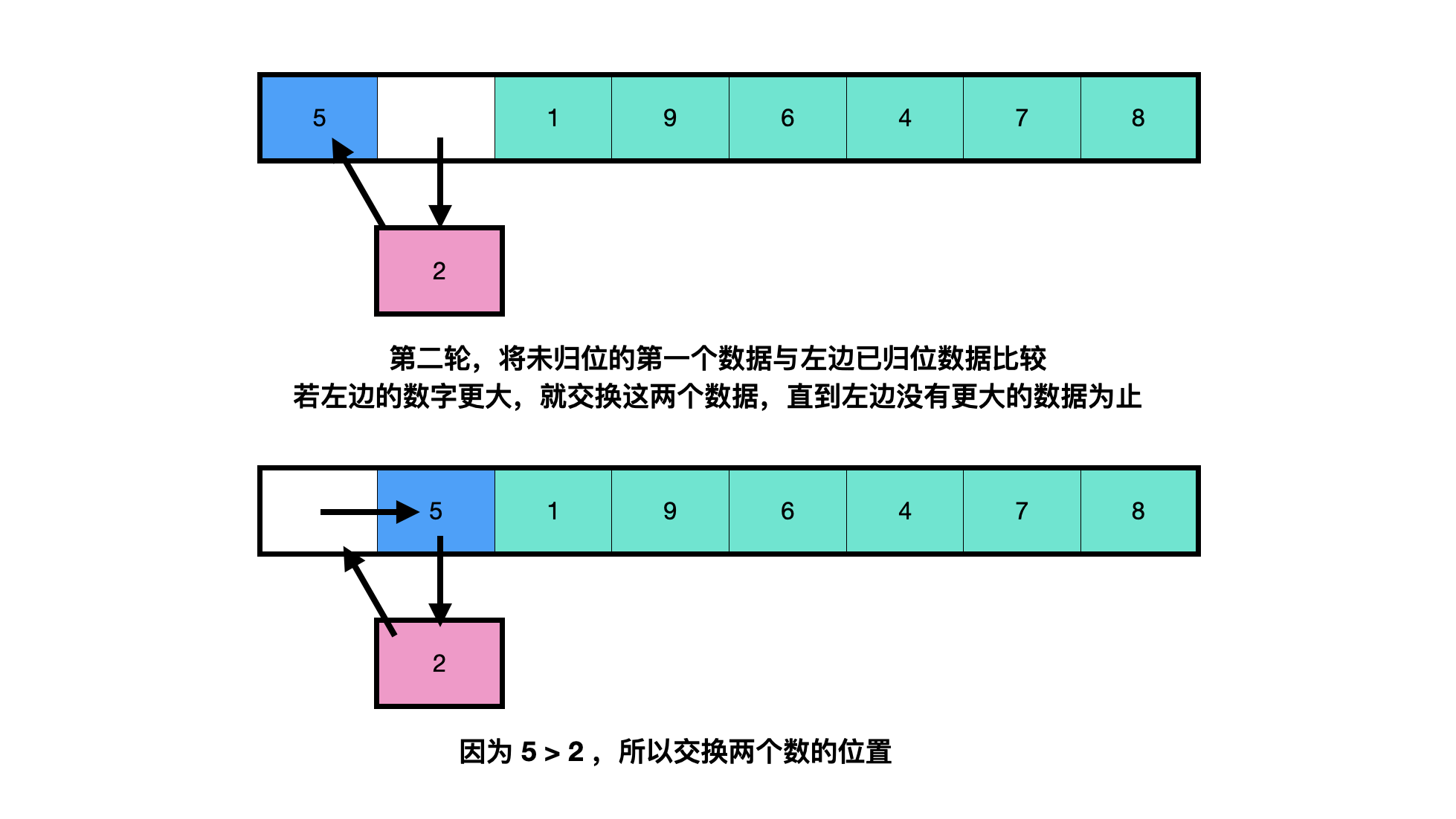
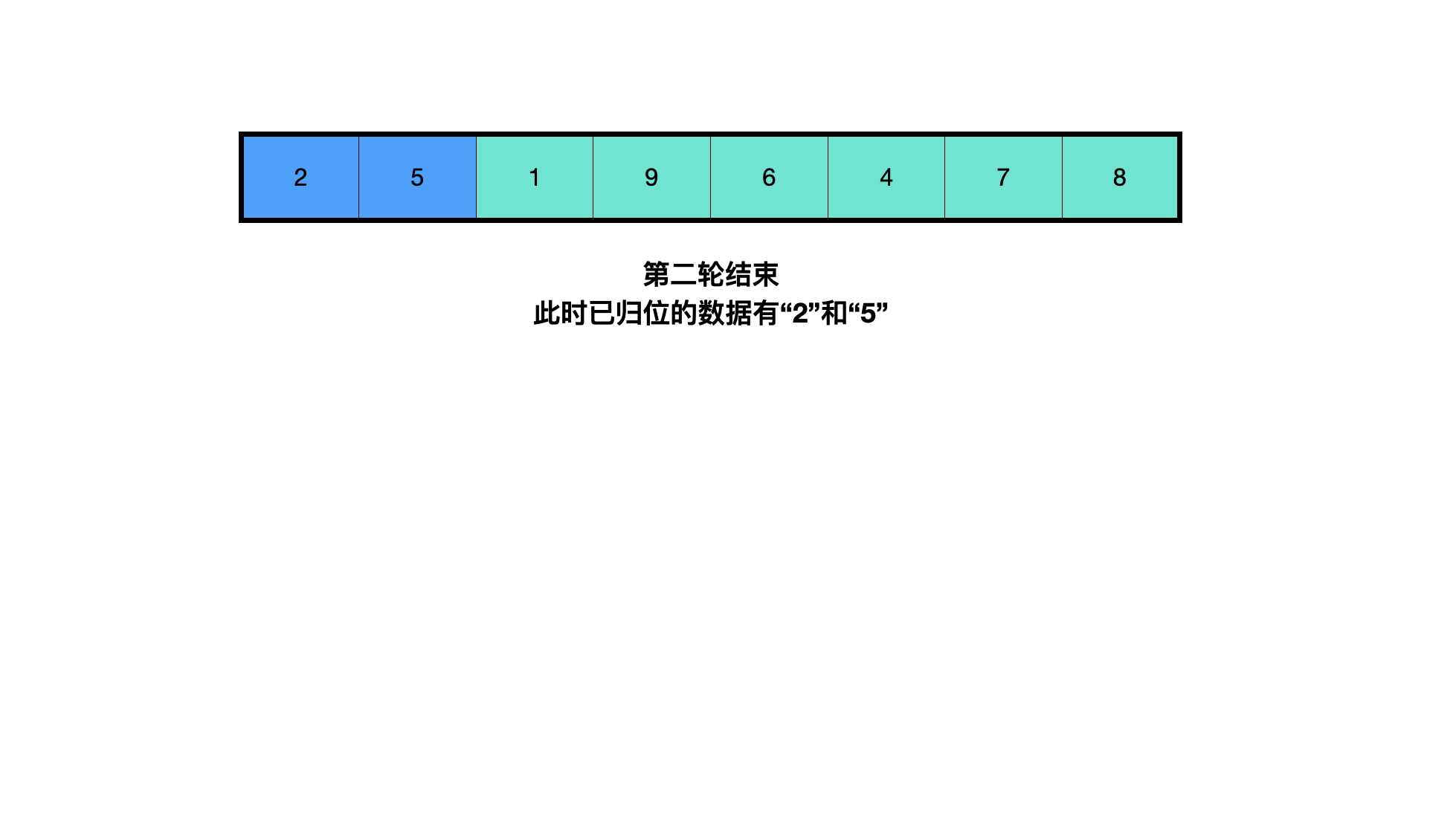
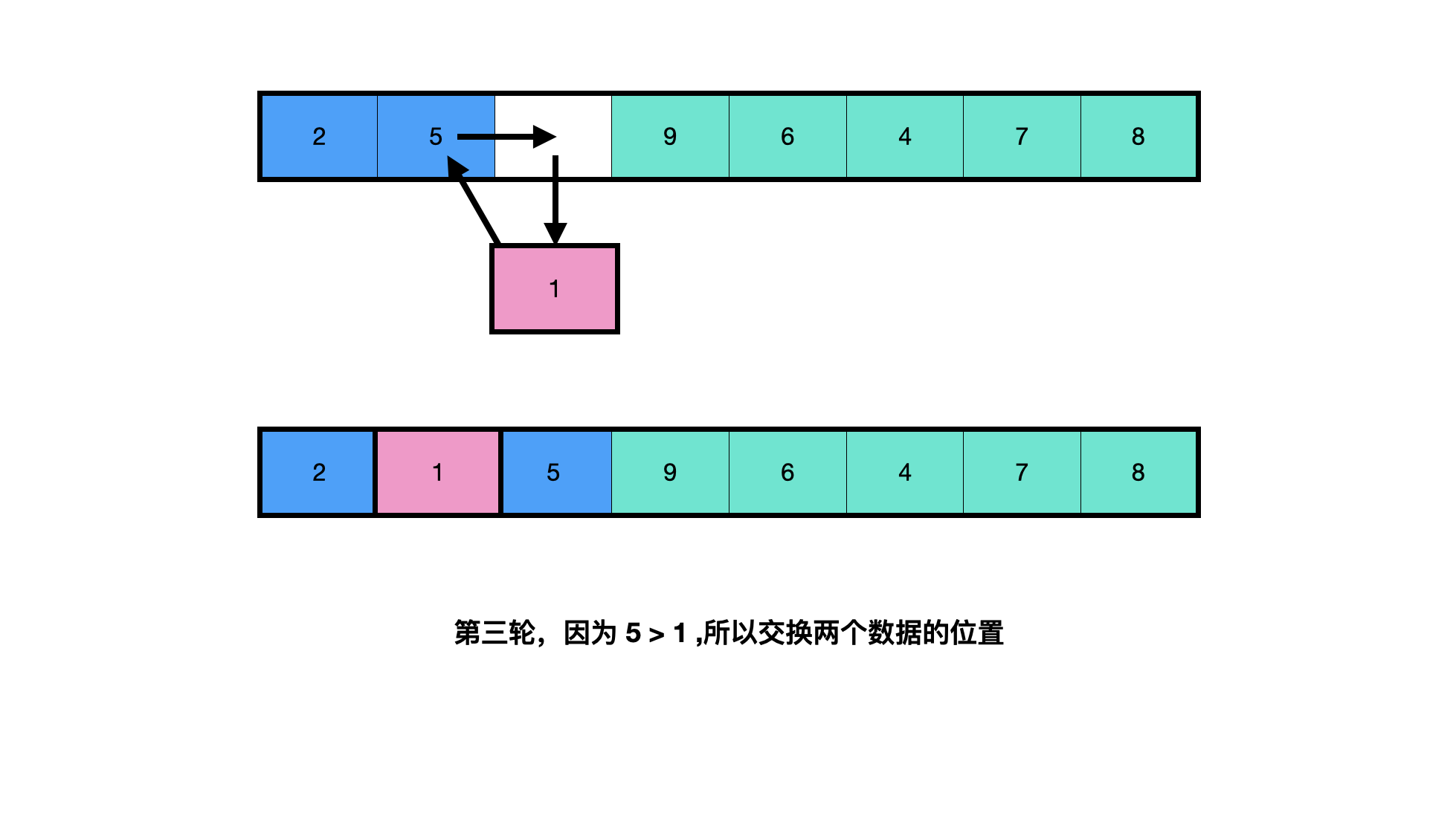
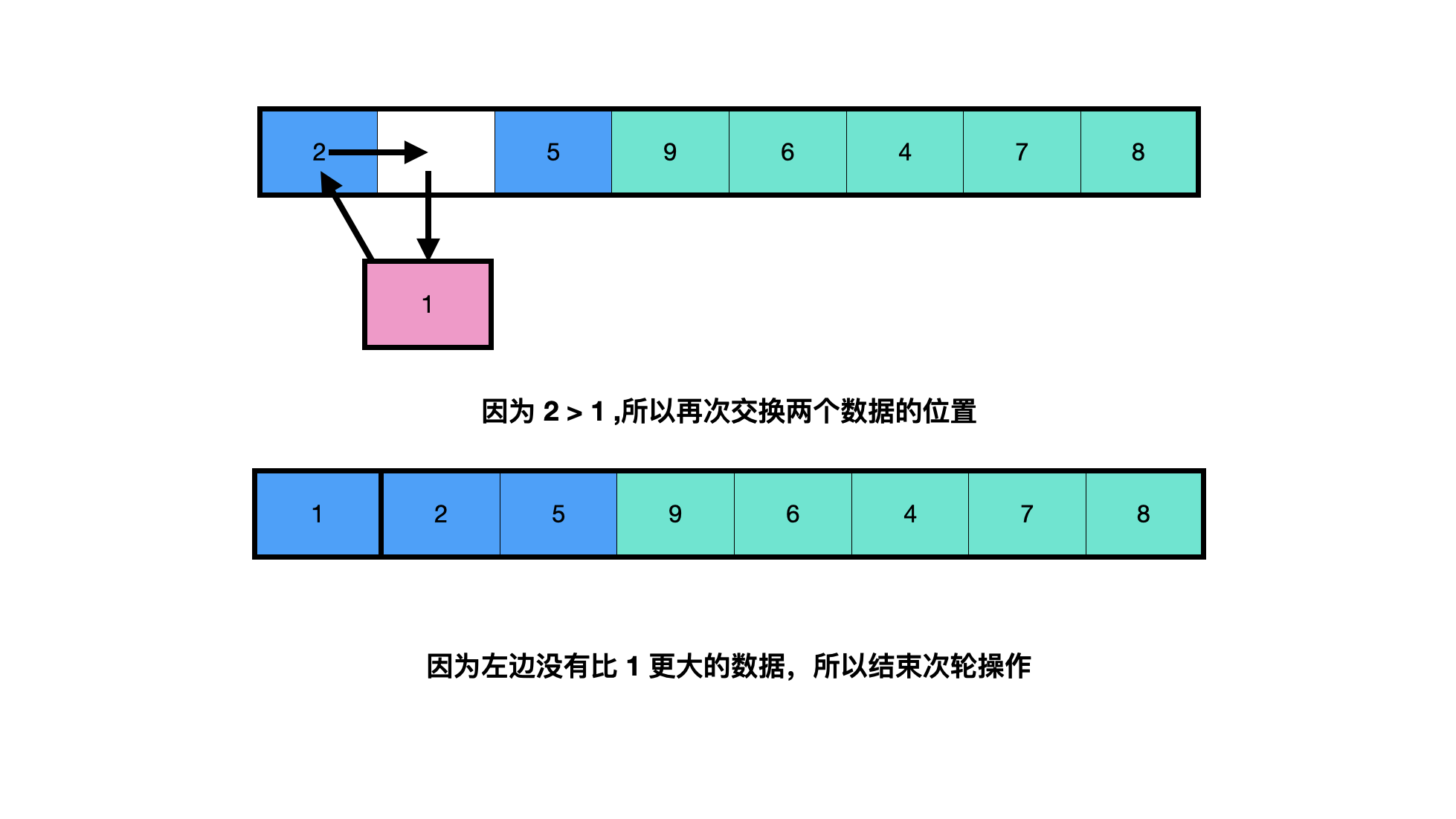
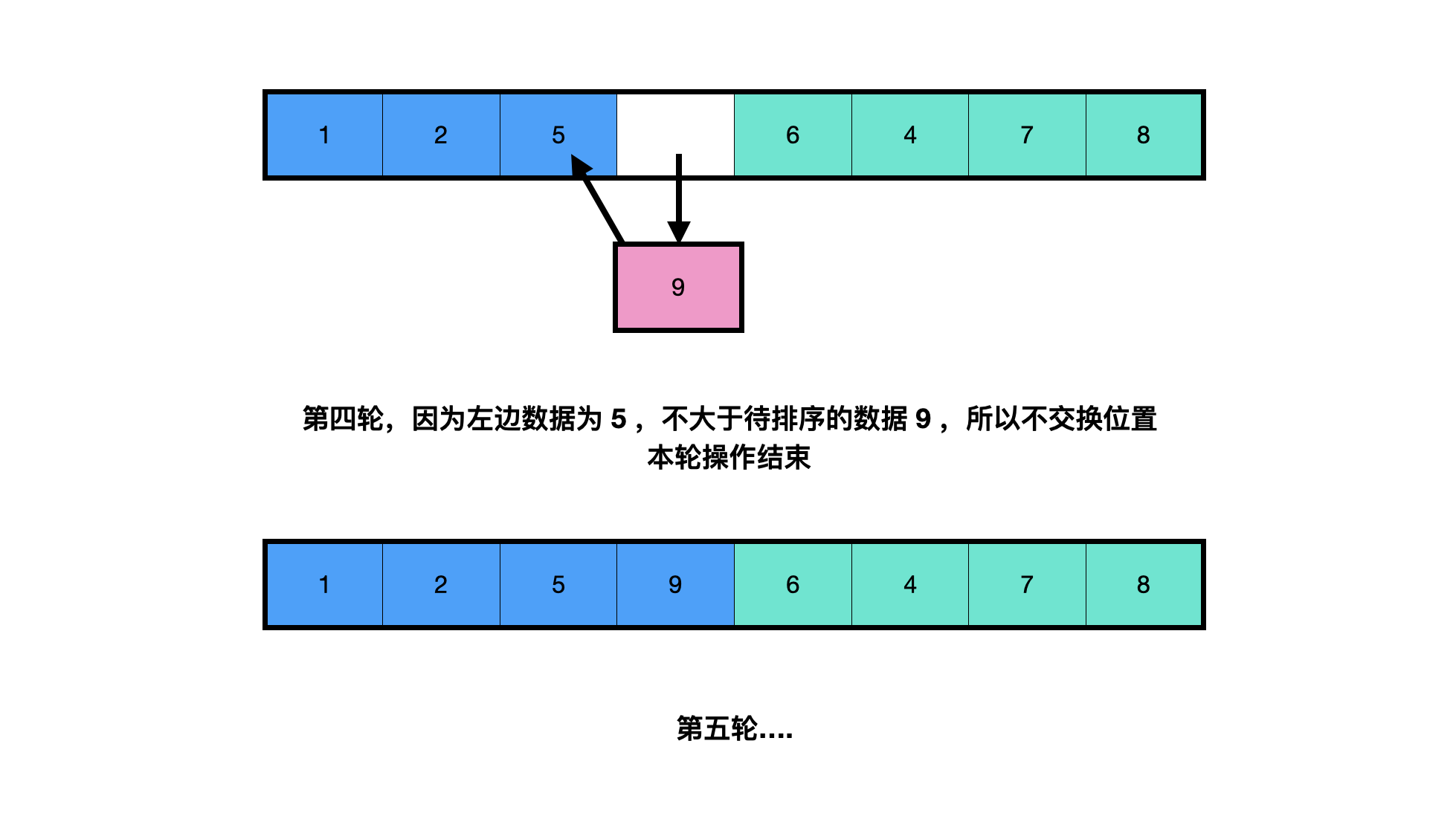
public class InsertionSort {
    public static void InsertionSort(int[] A) {
        int key = 0, flag = 0;
        for (int i = 1; i < A.length; i++) {
            key = A[i];                 //Store the number of exchanges in the key
            flag = i - 1;               //flag is a "pointer" to find a suitable position for the data to be exchanged in the homing part (i-1 is the rightmost data of the homing part)
            while (flag >= 0 && A[flag] > key) {//When the data pointed to by the pointer is greater than the key
                A[flag + 1] = A[flag];//Exchange data
                A[flag] = key;    //Reassign key
                flag--;               //Move the pointer to the left to prepare for the next comparison
            }
        }
    }
}

To insert sorting, you need to take out the data of the unordered part in turn and compare it with the data on the left (the returned part). If the data on the left is smaller during comparison, you don't need to compare again and end this round of operation directly. However, if the data extracted each time is smaller than all the data in the left (returned) part, it is a bad situation. Then n-1 operations are required when fetching data for the nth time. The time complexity is O(n2).

Merge sort

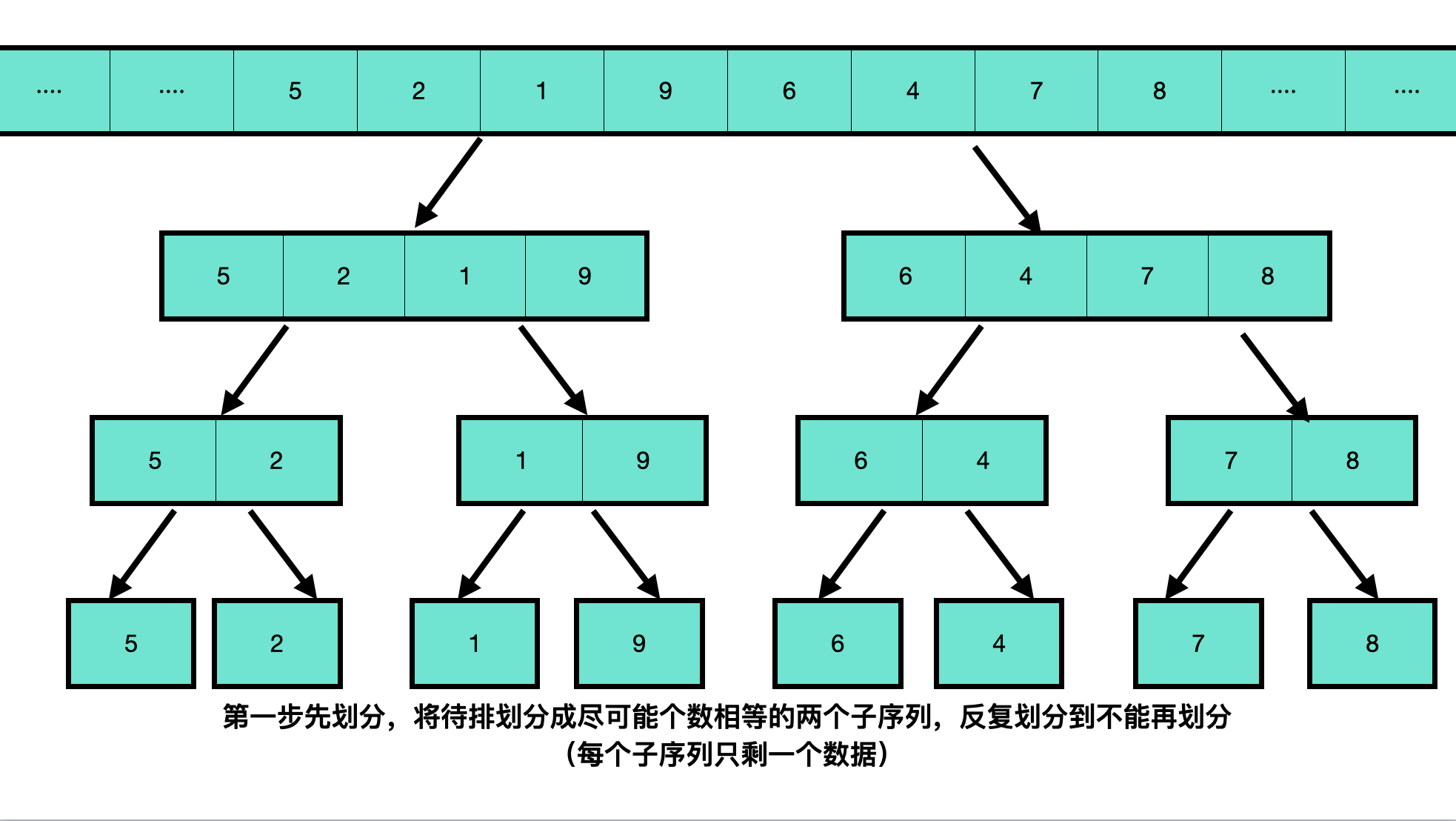
Merge sort divides the sequence to be sorted into two halves of equal length as far as possible. It ends when each subsequence has only one data. From the smallest subsequence, it is merged step by step into an ordered larger subsequence, and then merged into an ordered original sequence.

The division process is shown in the figure:

Consolidation process:

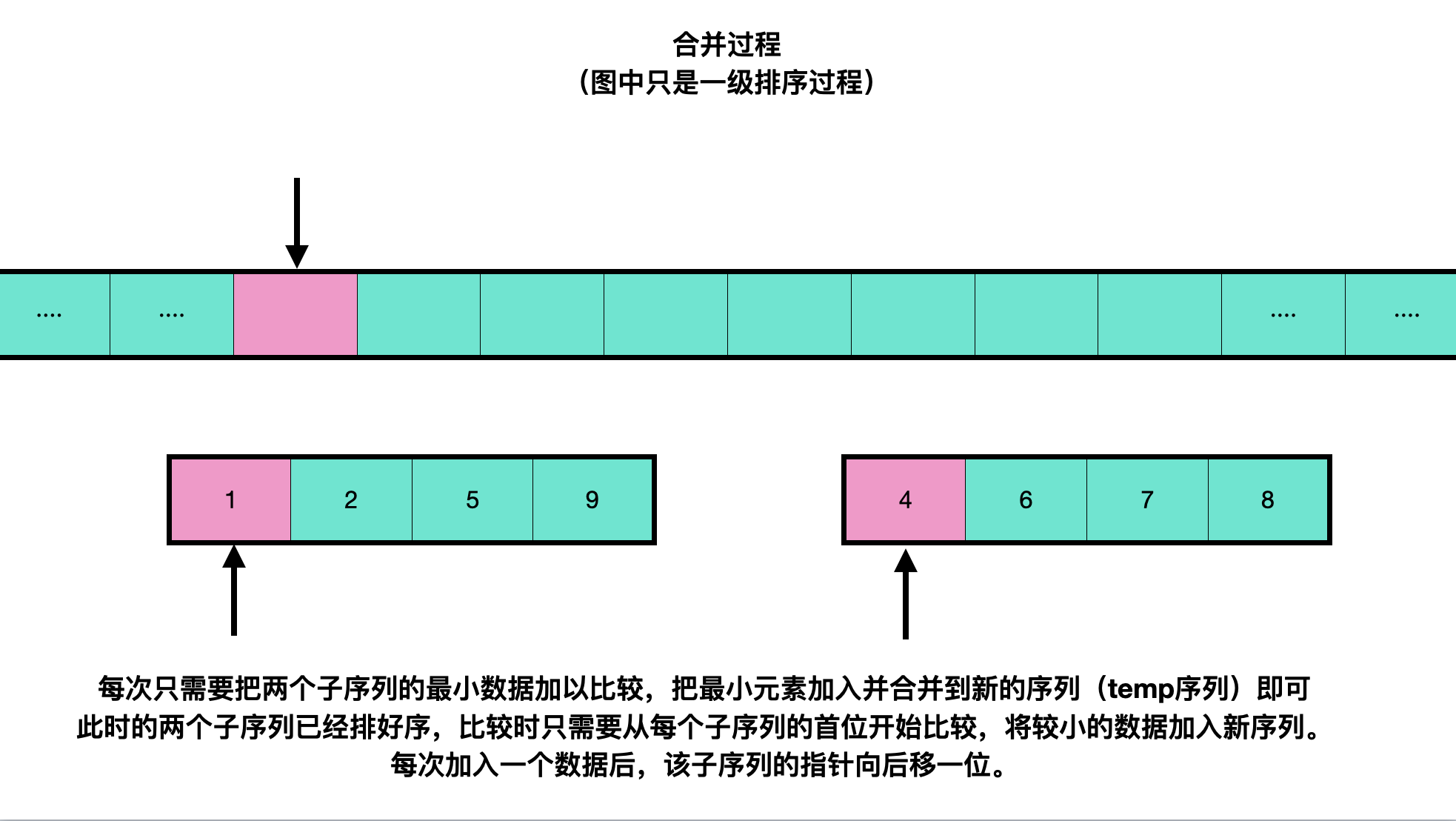
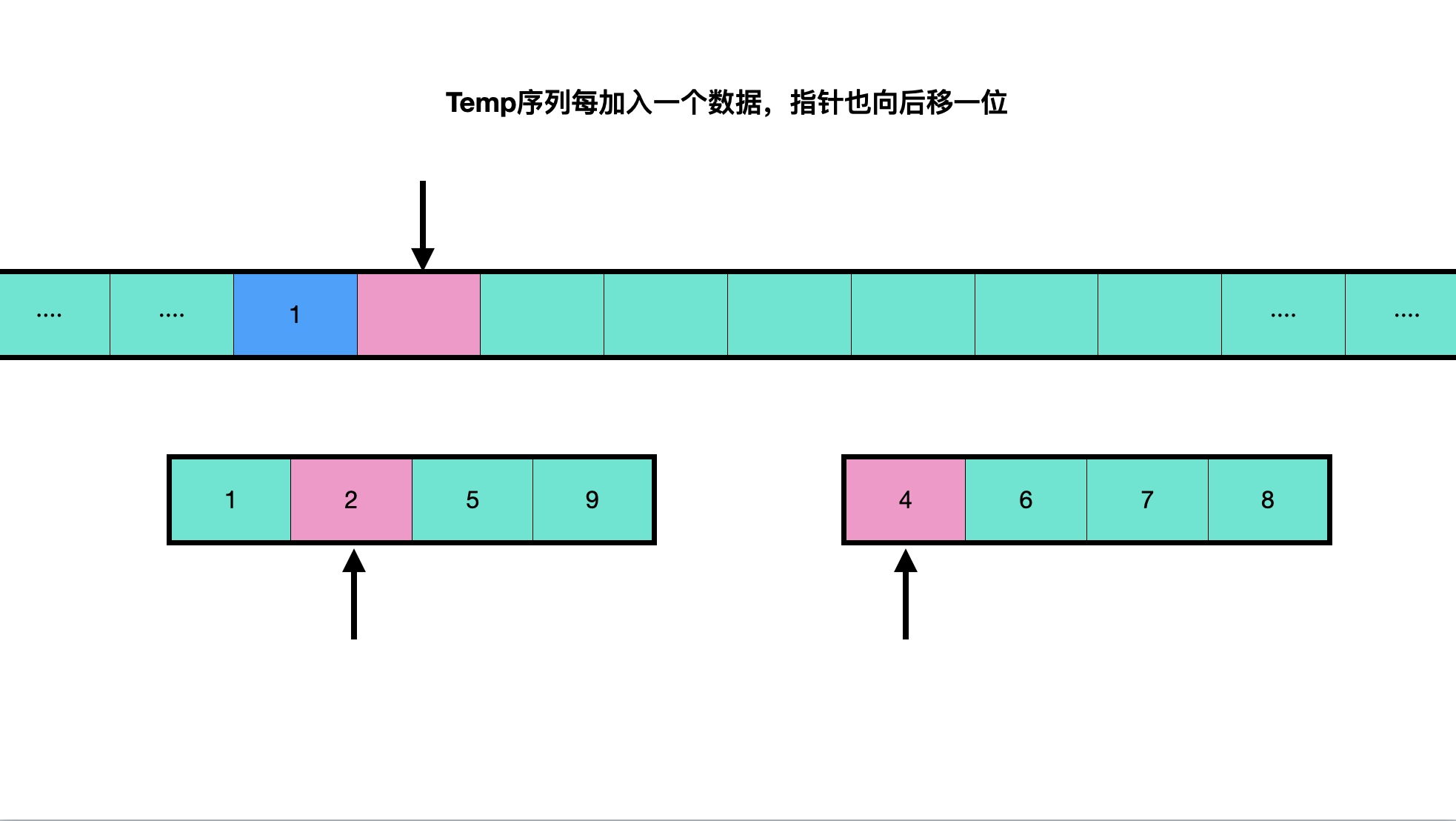
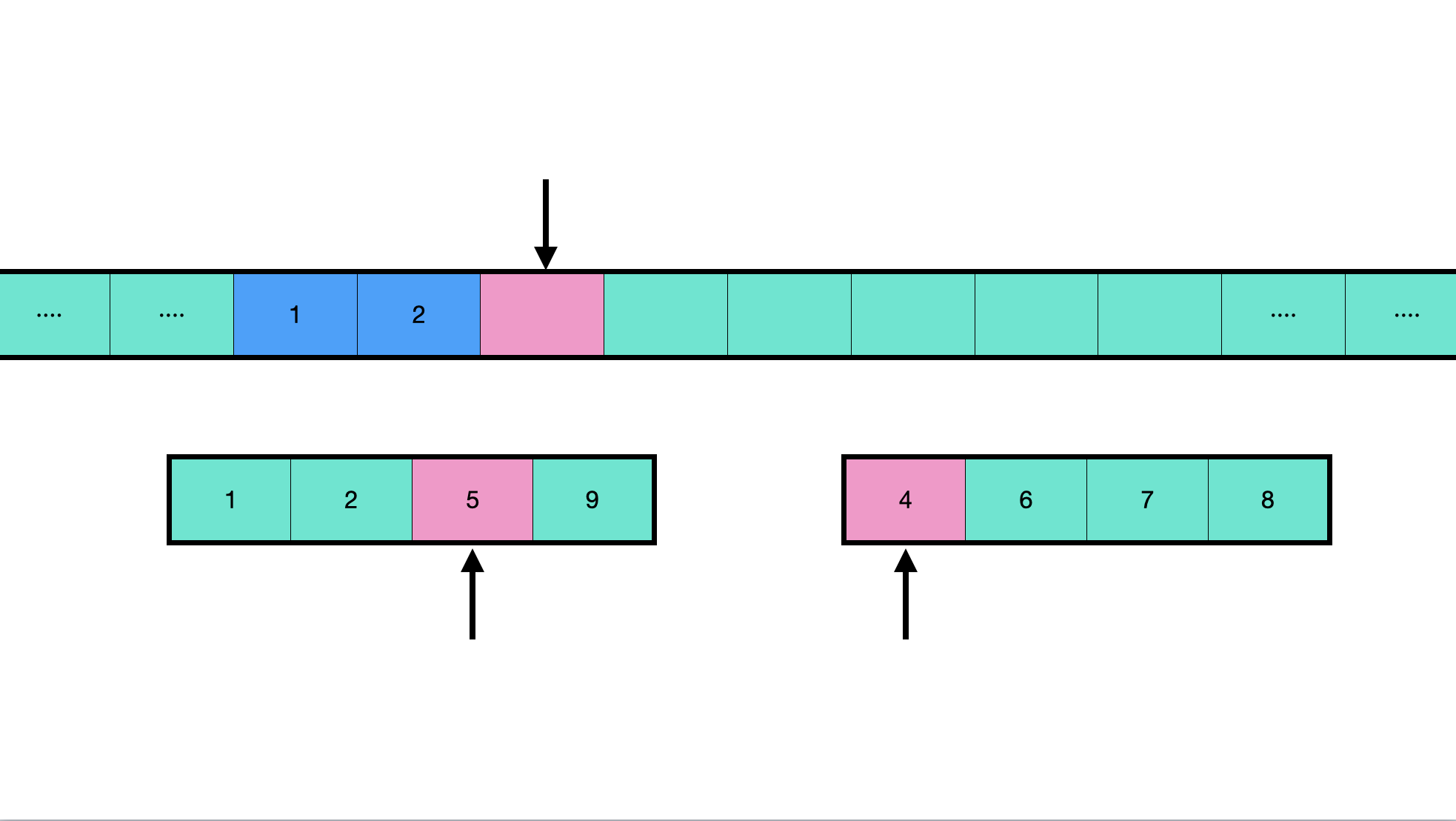
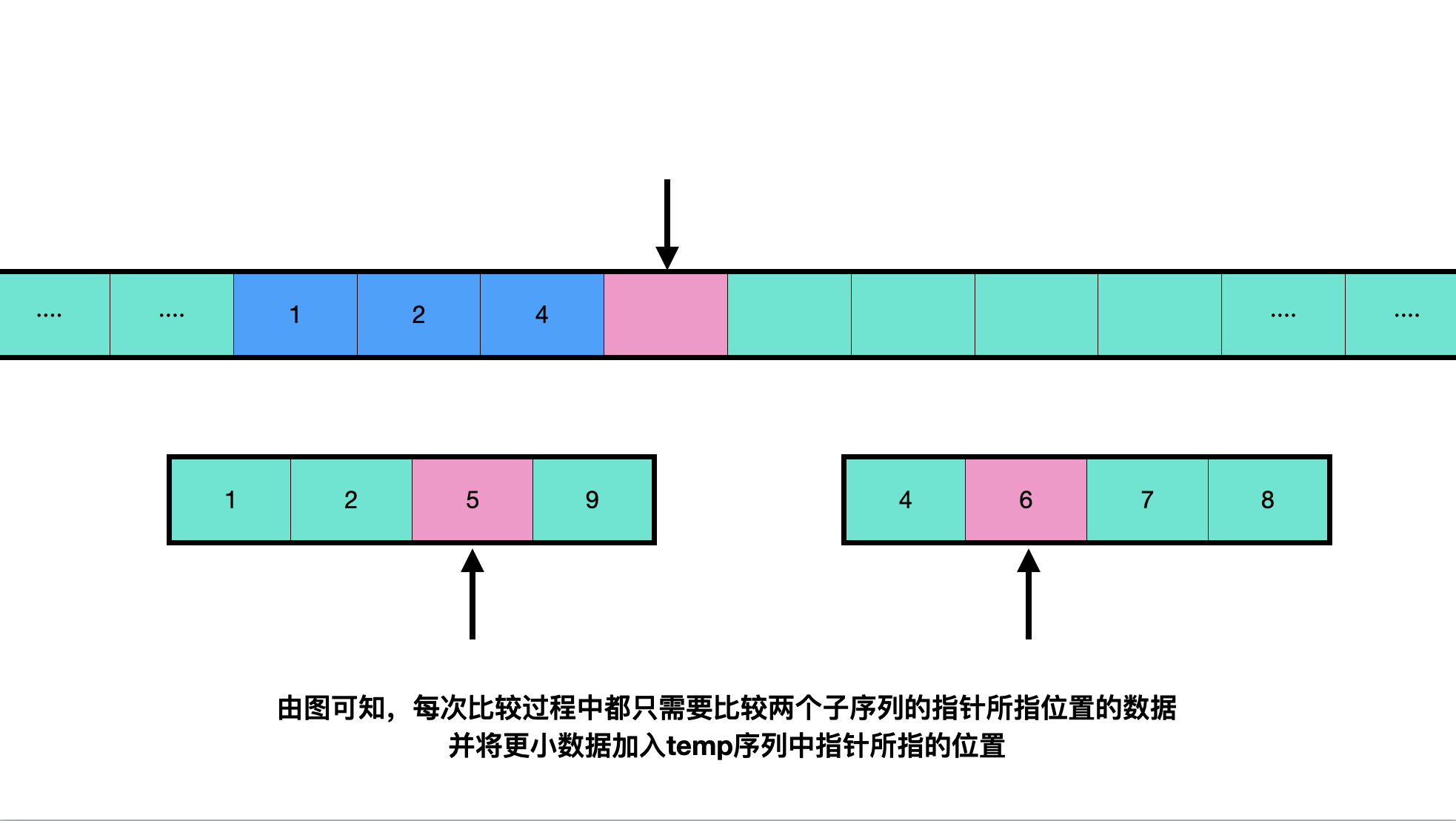
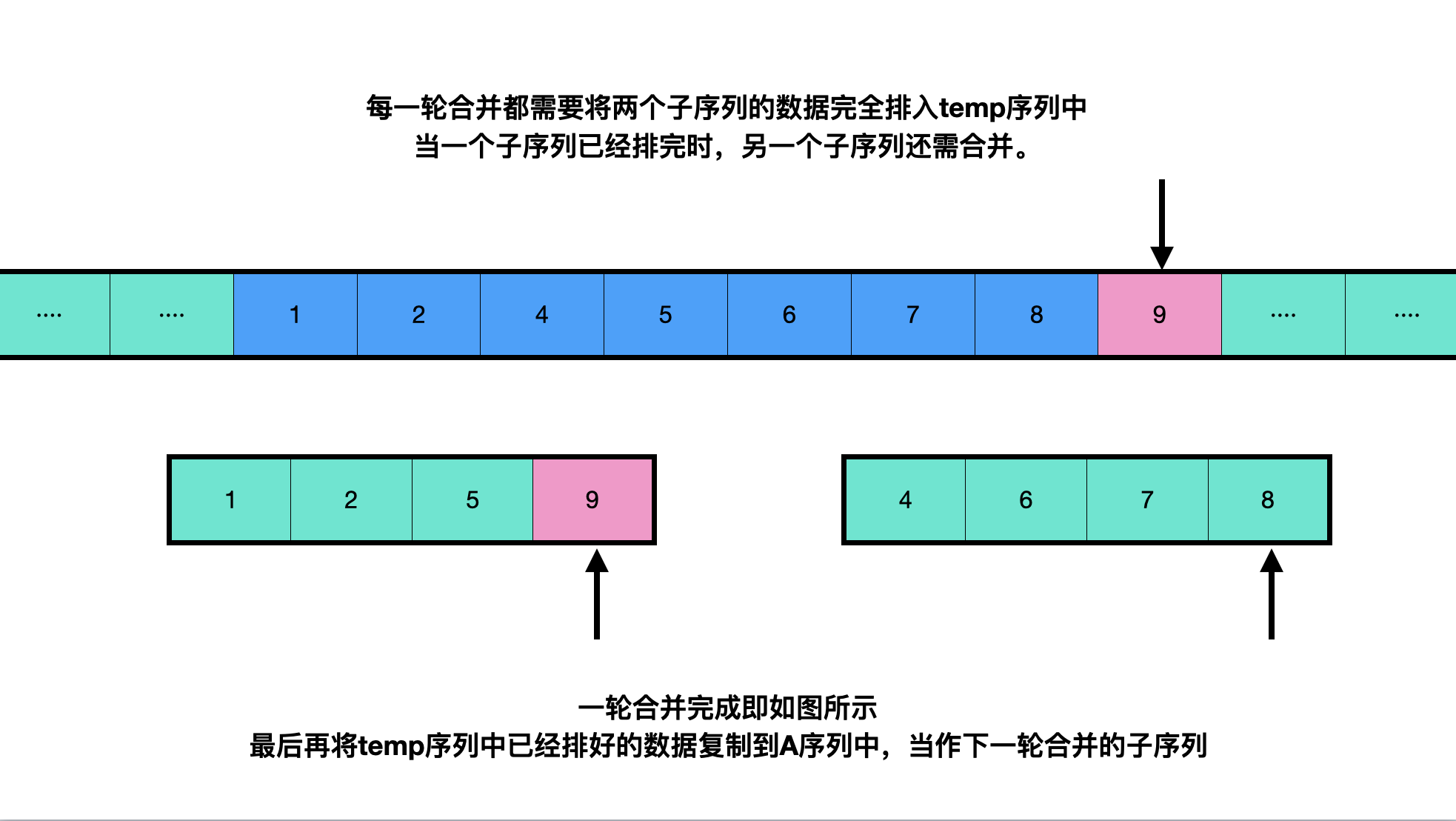
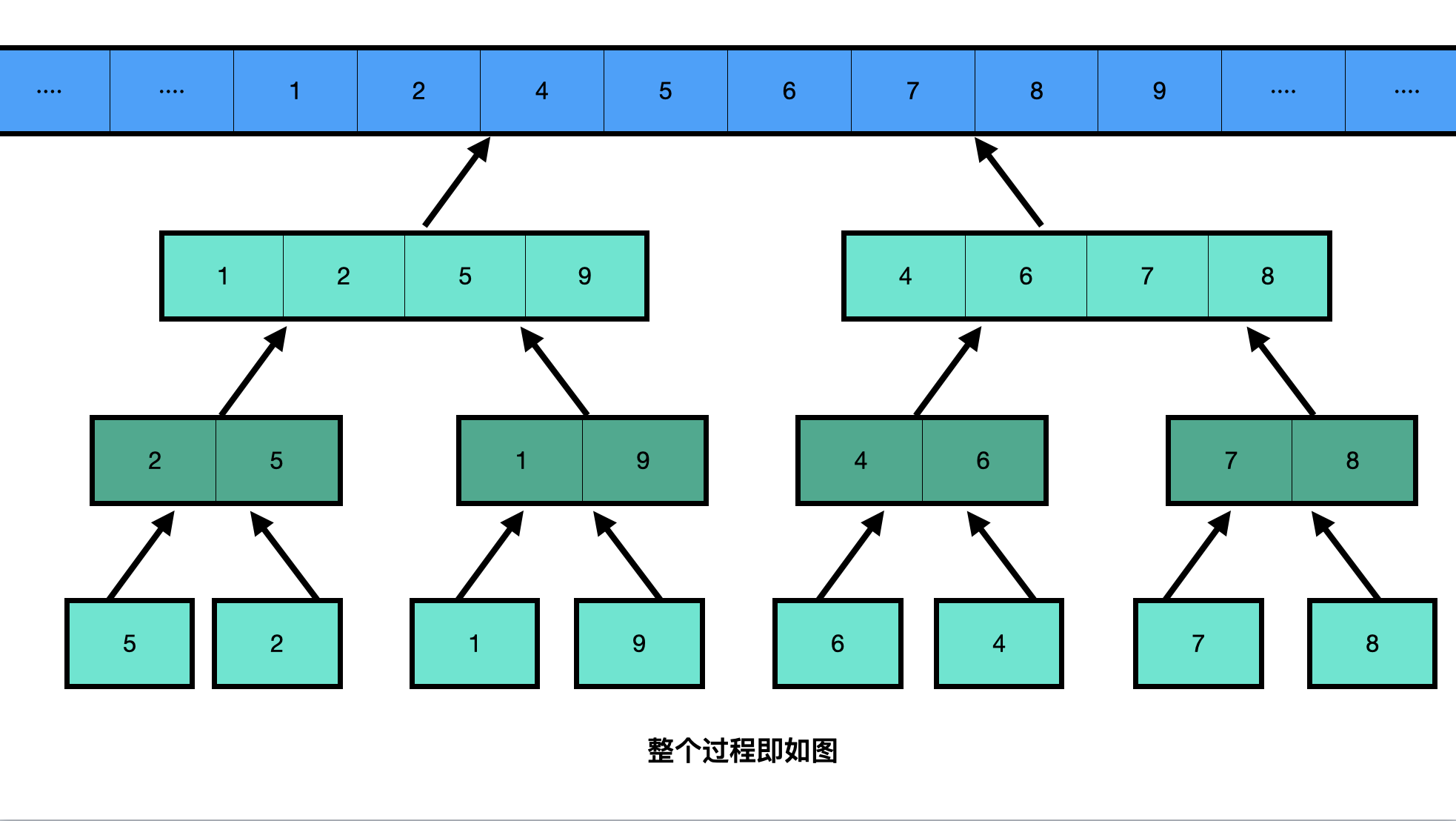
The code is as follows (from small to large):

public class MergeSort {
    public static void merge(int[] A,int left,int right,int[] temp){//A: Sort array, temp: additional array for temporarily storing data;
        if(right-left>1){
            //divide
            int m=left+(right-left)/2;//Divide it into two half arrays with equal number of elements as far as possible; m is the maximum subscript of the first half array ()
            int p=left,q=m,i=left;//p is the "pointer" (subscript) of the first half array, q is the "pointer" (subscript) of the second half array, and i is the "pointer" (subscript) of the additional array;
            //
            merge(A, left, m, temp);//Call recursive solution (divide the array and then merge) the first half
            merge(A, m, right, temp);//second half
            //merge
            while (p<m||q<right){//When the left and right half arrays have unconsolidated data in any array
                if(q>=right||p<m&&A[p]<=A[q])//Compare the size of the subscript data corresponding to the left and right half arrays in turn, and copy the small into the additional array;
                

For the merge sort process, the number of data in the sub sequences divided in each step is n, so the running time of each row is O(n). The sequence with length n can be divided into log2n times. Therefore, it can be known that the time complexity is O(nlogn).

thank

Finally, I would like to thank my classmates and friends who helped me in my study and writing process.
There may be mistakes in the content of the new blog for the first time. I hope readers and visitors can put forward it and let me correct it. Thank you for reading.