BZOJ questions

On this topic, Jin commemorates the first step of blogger's sprint to provincial election

 

Take a look, isn't this the bare minimum cut?

Min cut = = max flow;

Then 5 minutes code ISAP;

Hand it in... TLE... Muddle

And then a wave of optimization constants without eggs

(go to 1e6 fucking points, 3e6 sides!!!)

 

Asked Du Niang, only then knew this question graph is "the plan";

The minimum cut and maximum flow of a planar graph can be solved by transforming it into the shortest running path of a dual graph

So what is a dual graph?

Generally speaking, the dual graph is to change the points of the original graph into faces (areas surrounded by edges) and faces into points, while undirected edges connect the faces of the original graph;

As shown in the following figure, the blue one is the original, the red one is the dual, and the green one is the shortest path of the dual (the edge of s-t is deleted from the smallest ring) (also the minimum cut of the original);

 

 

 

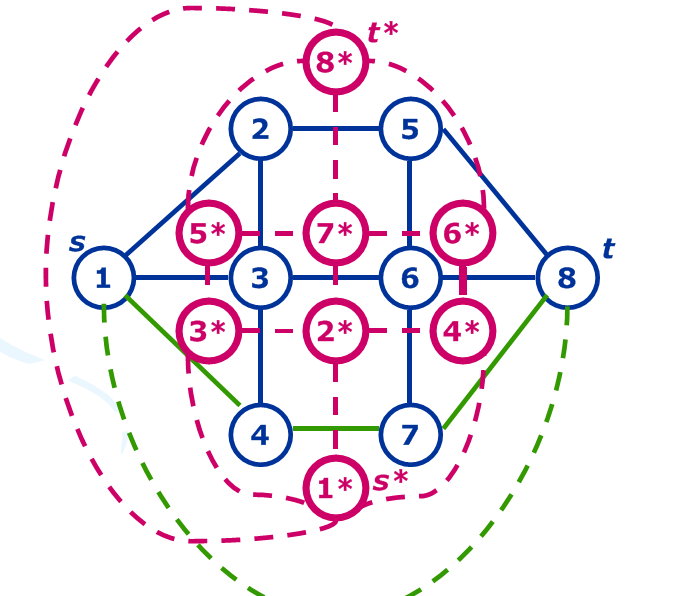
If you don't understand, please refer to—— Weekly winter Dalao<On the application of the maximum and minimum theorem in the competition of Informatics

Note: in the plan, there is an infinite surface outside;

Then you can run SPFA happily;

 

So, with this AC problem is not very simple

No, no, no, except for the construction drawings that can make you dizzy;

There is also a very, very pit in this question, not one of them!! (I checked 3 Days)

That is:

N = = 1 | M = = 1 | ah!! (MMP out of data)

 

AC Code:

 

 

#include<bits/stdc++.h>
using namespace std;
int dis[2000100],used[2000100],point[6000100];  // 2e6 points, 6e6 edges
int cnt;
queue<int>q;
struct edge{
    int u,v,next;
}e[6000100];
inline int read(){  // It's said that it's easy to read without speeding up TLE
    int x=0;
    char ch=getchar();
    while(ch>'9'||ch<'0') ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return x;
}
inline void ad(int x,int y,int z){
    e[++cnt].u=y;
    e[cnt].v=z;
    e[cnt].next=point[x];
    point[x]=cnt;
}
inline void add(int x,int y,int z){  // Boundless laziness...
    ad(x,y,z);
    ad(y,x,z);
}
int spfa(int s,int t){  // SPFA A board
    memset(dis,0x3f,sizeof(dis));
    q.push(s);
    used[s]=1;
    dis[s]=0;
    while(!q.empty()){
        s=q.front();
        q.pop();
        used[s]=0;
        for(int i=point[s];i;i=e[i].next)
            if(dis[e[i].u]>dis[s]+e[i].v){
                dis[e[i].u]=dis[s]+e[i].v;
                if(!used[e[i].u]){
                    used[e[i].u]=1;
                    q.push(e[i].u);
                }
            }
    }
    return dis[t];
}
int main(){
    int n,m,x,s=0;
    n=read(),m=read();
    if(n==1||m==1){  // Special judgment is very important!
        s=0x3fffffff;
        for(int i=1;i<max(n,m);i++){
            x=read();
            s=min(s,x);
        }
        printf("%d\n",s);
        return 0;
    }
    int t=2*(n-1)*(m-1)+1;  // t:End 
    for(int i=1;i<=n*(m-1);i++){
        x=read();
        add(min(2*i,t),max(0,2*(i-m)+1),x);  // Lateral edge
    }
    for(int i=1;i<=(n-1)*m;i++){
        x=read();
        s++;
        if(i%m!=0&&i%m!=1) s++,add(s-1,s,x);  // Longitudinal edge
        else if(i%m==0) add(s,0,x);
        else add(t,s,x);
    }
    for(int i=1;i<=(m-1)*(n-1);i++){
        x=read();
        add(2*i-1,2*i,x);  // Oblique edge
    }
    printf("%d\n",spfa(0,t));
    return 0;
}

 

 

By The_Seventh

2017-12-24  11:19:04