bzoj 1913 signaling signal coverage

Description

Input

The first line of input contains a positive integer n representing the total number of houses.Next, there are n rows representing the location of each house.For i = 1, 2,.., n, the coordinates of the ith house are represented by a pair of integers xi and yi separated by a space.
Output

The output file contains a real number indicating how many houses are covered by the signal on average, and the absolute error between the output and the exact value should not exceed 0.01.
Sample Input

4
0 2
4 4
0 0
2 0
Sample Output

3.500
HINT

3.5, 3.50, 3.500,...Any of the outputs are correct.In addition, 3.49, 3.51,
3.499999,...And so on are also acceptable outputs.
[Data Range]
100% of the data guarantees that for i = 1, 2,.., n, the coordinates of the ith house (xi, yi) are integers and
- 1,000,000 < xi, yi < 1,000,000. Any three houses are not in the same straight line, and no four houses are
On the same circle;
40% of data, n < 100;
70% of data, n < 500;
100% of data, 3 < n < 1,500.

Topic: n points on a plane, randomly select 3 points to form a circle. Ask how many points you want in the circle and on the circle.The data is guaranteed to have no 4-point circle, 3-point line and focus.

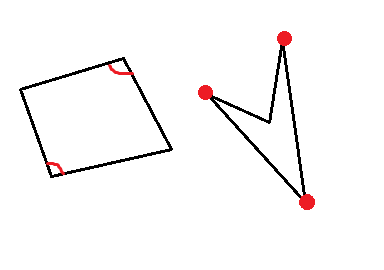
Ideas:
Considering a quadrilateral, a convex quadrilateral contributes 2 to the answer and a concave quadrilateral contributes 1 to the answer.Since there is no four-point common circle (no square), at least one corner in a convex quadrilateral must be blunt, then the blunt point and the circle formed by its two adjacent points, if they contain one remaining point, then the circle formed by the remaining three points must also contain the blunt point, and the other two circles will contribute.So a convex quadrilateral contributes 2 to the answer.In a concave quadrilateral, only a circle formed by three points outside can contain one point inside.So a concave quadrilateral contributes 1 to the answer.
If the number of concave quadrilateral is a and the number of convex quadrilateral is b, then b=C(n, 4) - a.How do we calculate a concave-convex quadrilateral?Consider enumerating the middle point X of a concave quadrilateral, with the middle point as the origin. As long as the other three points found form a triangle that does not contain the origin, it is a set of convex quadrilateral.So we enumerate a point p[i], and set x-p[i] as the right-most edge from X. It is easy to see that if only two points remain on the same side of the line x-p[i], it is a convex quadrilateral.So when x and p[i] are fixed, the number of convex quadrilateral is the logarithm of points that meet the criteria.Polar ordering enumerates two edges whose polar difference is just less than pi, so the point between them and the point on one of them (excluding the middle point) satisfy the criteria.
We are glad to find that the vast majority of points between the two states x-p[i] and x-p[i+1] are duplicated when enumerating in the order of polar angles.Then the time complexity of the enumeration is O(n).Magical!!!
The final expectation is (a+2*b)/C(n,3).

Hot chicken I was naive at first to cross by row pole, but the origin is not necessarily in the lower left corner, so sorting can be conflicting.It was after the God of membranes that we discovered atan2, a magical function of returning azimuth.

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#define LL long long 
using namespace std;

LL A, B, n;

struct Node{
    LL x, y;
    double angel;
}a[1510], p[1510];

LL operator*(Node a, Node b){
    return a.x*b.y - a.y*b.x;
}

Node operator-(Node a, Node b){
    return (Node){a.x-b.x, a.y-b.y};
}

double get_angel(Node a){
    return atan2(a.y, a.x);//atan2 function sorted by azimuth 
}

bool operator<(Node a, Node b){
    return a.angel < b.angel;
}

/*bool operator<(Node aa, Node bb){
    return ((aa - p[0]) * (bb - p[0])) > 0.0;
}*/WA

LL C(int m, int n){//Number of combinations 
    LL rt = 1;
    for(int i=1; i<=n; i++)
        rt *= m-i+1;
    for(int i=1; i<=n; i++)
        rt /= i;
    return rt;
}

LL solve(int x){
    LL tot = C(n-1, 3);//C(n-1,3) triangles/quadrilateral can be found when n-1 points are removed from the enumeration point 
    int top = 0;
    for(int i=1; i<=n; i++){
        if(i != x) p[++top] = a[i];
        else p[0] = a[i];//origin 
    }
    for(int i=1; i<=top; i++) p[i].angel = get_angel(p[i] - p[0]);
    sort(p+1,p+top+1);
    int R=2, t=0;
    for(int i=1; i<=top; i++){
        while((p[i]-p[0]) * (p[R]-p[0]) >= 0){//Fixed x-p[i] to ensure that all p[R] are on one side
        //So the triangle of any two p[R] and p[i] does not contain x, i t is a convex quadrilateral (no three-point collinearity) 
            R = R % top + 1; t++;
            if(R == i) break;//Avoid duplication because i is to be enumerated once 
        }
        tot -= C(t, 2);//Has C(t, 2) convex quadrilateral 
        t--;//Move one point at a time after sorting and run to x-p[i] to remove (no three points collinear), the other t-1 points must be satisfied 
    }
    return tot;
}

int main(){
    scanf("%lld", &n);
    if(n == 3){ puts("3.00"); return 0; }
    for(int i=1; i<=n; i++)
        scanf("%lld%lld", &a[i].x, &a[i].y);
    for(int i=1; i<=n; i++) 
        A += solve(i);
    B = C(n, 4) - A;
    double ans = 2*B+A;//Total contribution 
    ans /= C(n, 3);//C(n, 3) circles 
    printf("%0.6lf", ans+3.0);//Each circle originally contains three points 
    return 0;
}