Binary search tree

The concept of binary search tree and its illustration

Binary search tree, also known as binary sort tree, is either an empty tree or a binary tree with the following properties:

• If its left subtree is not empty, the value of all nodes on the left subtree is less than that of the root node
• If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of the root node
• Its left and right subtrees are also binary search trees

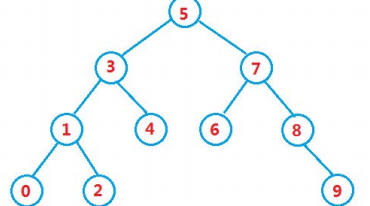
All its nodes are printed out as ordered sequences through medium order traversal.

Search tree operation

First, the search tree is a special tree. We have to define its structure first
And initialize it

template<class K>
struct BSTreeNode
{
	K _key;
	BSTreeNode* _left;
	BSTreeNode* _right;

	BSTreeNode(K& key)
		:key(_key), _left(nullptr), right(nullptr)
	{}
};

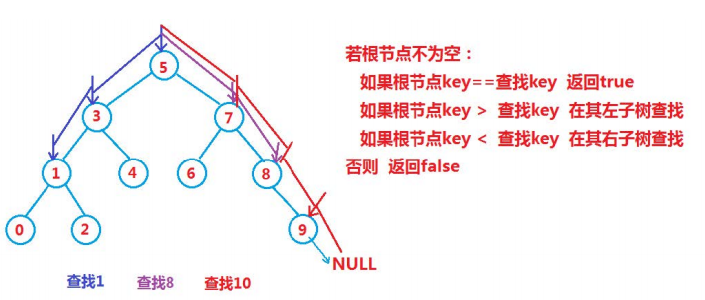
lookup

The search is relatively simple, because the search tree is ordered and the key value can be judged directly.

Node* Find(K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}

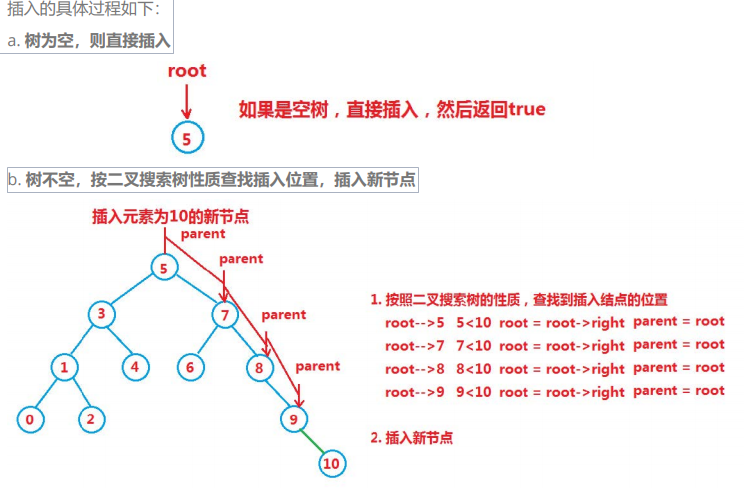
insert

Here, we first pass in the inserted key value and push it to the type through the template.
If the incoming tree is empty, we need to insert the currently inserted node
When we are not, we need to constantly judge the size until we find the current corresponding position to insert it

bool Insert(K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
				return false;
		}
		Node* newnode = new Node(key);
		if (parent->_key>key)
		{
			parent->_left = newnode;
		}
		else if (parent->_key < key)
		{
			parent->_right = newnode;
		}
		return true;
	}

delete

Deletion here is the most important and frequently tested.
Case A: delete the node and make the parent node of the deleted node point to the left child node of the deleted node
Case B: delete the node and make the parent node of the deleted node point to the right child node of the deleted node
Case C: find the first node in the middle order in its right subtree (with the smallest key), fill its value into the deleted node, and then deal with the deletion of the node

First find the corresponding deleted node and save the location of the previous node, and then make the previous node point to the leaf of the deleted node or delete the replaced node by deleting or replacing the node.

bool Erase(K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else if (cur == parent->left)
					{
						parent->_left = cur->_left;
					}
					else if (cur == parent->_right)
					{
						parent->_right = cur->_left;
					}
				}
				else
				{
					Node* newparent = cur;
					Node* submin = cur->_right;
					while (submin->_left)
					{
						newparent = submin;
						submin = submin->_left;
					}
					cur->_key = submin->_left;
					if (submin == newparent->_left)
					{
						newparent->_left = submin->_right;
					}
					else if (submin == newparent->_right)
					{
						newparent - _right = submin->_right;
					}
					delete submin；
				}
				return true;
			}
		}
		return false;
	}

performance analysis

Application of binary search tree

1. K model: in K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched.
2. KV model: each key has its corresponding Value value, that is, the key Value pair of < key, Value >. This method is very common in real life: for example, an English Chinese dictionary is the corresponding relationship between English and Chinese. The corresponding Chinese can be quickly found through English, and the English word and its corresponding Chinese < word, Chinese > constitute a key Value pair; Another example is to count the number of words. After successful statistics, the number of occurrences of a given word can be quickly found. The word and its number of occurrences are < word, count > to form a key Value pair.

And binary search tree

The difference here is that each KEY value is bound with value.
When we find the key, we find the value corresponding to the value

template<class K, class V> 
struct BSTNode 
 { 
BSTNode(const K& key = K(), const V& value = V()) 
        : _pLeft(nullptr) , _pRight(nullptr), _key(key), _Value(value)     {} 
BSTNode<T>* _pLeft; 
BSTNode<T>* _pRight; 
K _key; 
V _value 
 };

Here you need to make some modifications to the constructor and add the value.

When inserting, you also need to pass in key and value. Of course, the search tree is also arranged by key instead of value. It can be found or deleted only by binding