Binary search tree
The concept of binary search tree
Binary search tree is also called binary sort tree (because the data is ordered in the middle order). It is either an empty tree or a binary tree with the following properties.
- If its left subtree is not empty, the values of all nodes on the left subtree are less than those of the root node
- If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
- Its left and right subtrees are also binary search trees
That is, in each subtree, the value in the left subtree is less than the root, and the value in the right subtree is greater than the root.
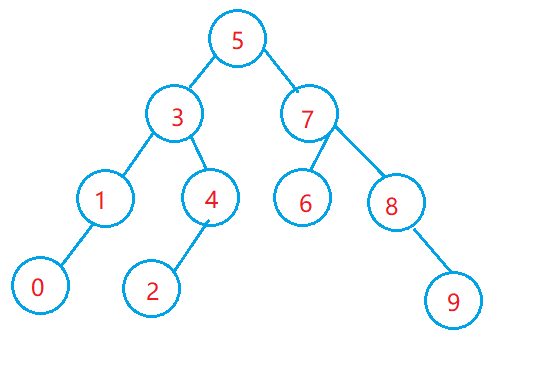
For example, int a[]={5,3,4,1,7,8,2,6,0,9};
Its time complexity is extreme O ( n ) O(n) O(n).
Only when the shape of the tree is close to a complete binary tree or a full binary tree can it be achieved l o g ( n ) log(n) log(n).
Therefore, in practice, there is no way to ensure the efficiency of search binary tree in extreme cases, so it is necessary to further explore the feature extension of search Binary Tree: AVLTree red black tree
They put forward requirements for the left and right height of the search binary tree, which is very close to the complete binary tree, and their efficiency can be achieved O ( n ) O(n) O(n).
The above is generally used for searching in memory. When the data is on disk (external search), it further requires the tree height, and further derives B tree and B + tree. B tree series belongs to multi fork balanced tree.
Time complexity of addition, deletion, query and modification O ( n ) O(n) O(n).
Binary search tree operation
definition
#include<iostream>
#include<string>
using namespace std;
template <typename K>
struct BSTreeNode
{
public:
BSTreeNode* _left;
BSTreeNode* _right;
BSTreeNode(K key)
:_left(nullptr),
_right(nullptr),
_key(key)
{ }
K _key;
};
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
//For deep and shallow copies, the copy structure operator = needs to be implemented
private:
Node* _root;
};
Non recursive version
insert
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
//For deep and shallow copies, the copy structure operator = needs to be implemented
bool Insert(const K& key)
{
if( _root == nullptr )
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while( cur )
{
if( cur->_key < key )
{
parent = cur;
cur = cur->_right;
}
else if( cur ->_key > key )
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(key);
if( parent ->_key < key )
{
parent ->_right = cur;
}
else parent ->_left = cur;
return true;
}
private:
Node* _root;
};
Middle order traversal
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
//For deep and shallow copies, the copy structure operator = needs to be implemented
bool Insert(const K& key)
{
if( _root == nullptr )
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while( cur )
{
if( cur->_key < key )
{
parent = cur;
cur = cur->_right;
}
else if( cur ->_key > key )
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(key);
if( parent ->_key < key )
{
parent ->_right = cur;
}
else parent ->_left = cur;
return true;
}
void _InOrder(Node* root){
if(root == nullptr) return;
_InOrder(root->_left);
cout<<root->_key<<endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root;
};
int main()
{
BSTree<int>t;
int a[]={5,3,4,1,7,8,2,6,0,9};
for(auto e :a)
{
t.Insert(e);
}
t.InOrder();
return 0;
}
lookup
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
//Involving deep and shallow copies, it is necessary to implement copy construction, operator = and so on
bool Insert(const K& key)
{
if( _root == nullptr )
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while( cur )
{
if( cur->_key < key )
{
parent = cur;
cur = cur->_right;
}
else if( cur ->_key > key )
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(key);
if( parent ->_key < key )
{
parent ->_right = cur;
}
else parent ->_left = cur;
return true;
}
Node* Find(const K& key)
{
Node* cur =_root;
while(cur){
if( key >cur -> _key ) cur = cur -> _right;
else if( key < cur-> _key) cur = cur ->_left;
else return cur;
}
return nullptr;
}
void _InOrder(Node* root){
if(root == nullptr) return;
_InOrder(root->_left);
cout<<root->_key<<endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root;
};
delete
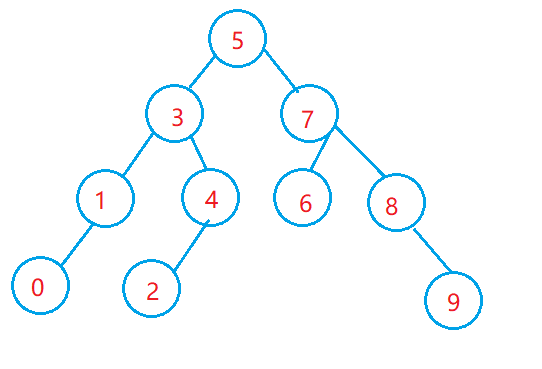
Delete a node with a value equal to key and analyze it by case.
- 6, 9, 0... To be deleted is very easy to handle. Features: leaf nodes.
- Delete the current node and set the child node corresponding to the father as the wild pointer.
- The node to be deleted is 8,1... OK. Features: only one child
- Delete the current node, give the child to the father of the current node and replace him.
- To delete is 5, 7. Features: two children.
- Solution: replace to delete.
- Go to the child to find a node whose value can replace its own position and delete it by itself.
- The largest node of the left subtree - the rightmost node of the left subtree is the largest
- The smallest node of the right subtree - the leftmost node of the right subtree is the smallest
- After these two nodes are replaced, they both conform to feature 1 or feature 2 and can be deleted directly.
- Further analysis, the processing of feature 1 can be processed by the method of feature 2. Therefore, only feature 2 and feature 3 are processed.
For the case of deleting feature 2, consider the details in the following figure
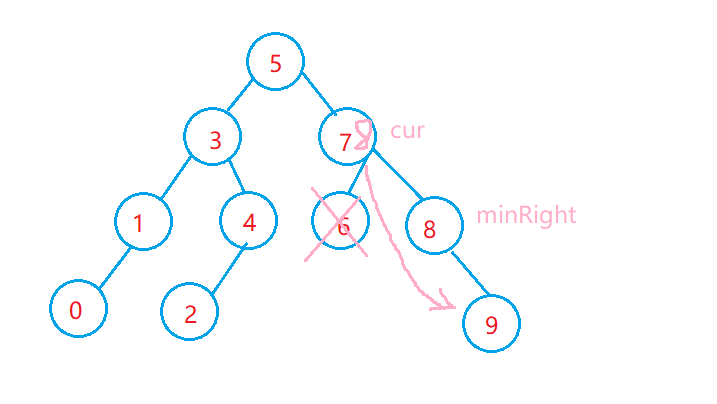
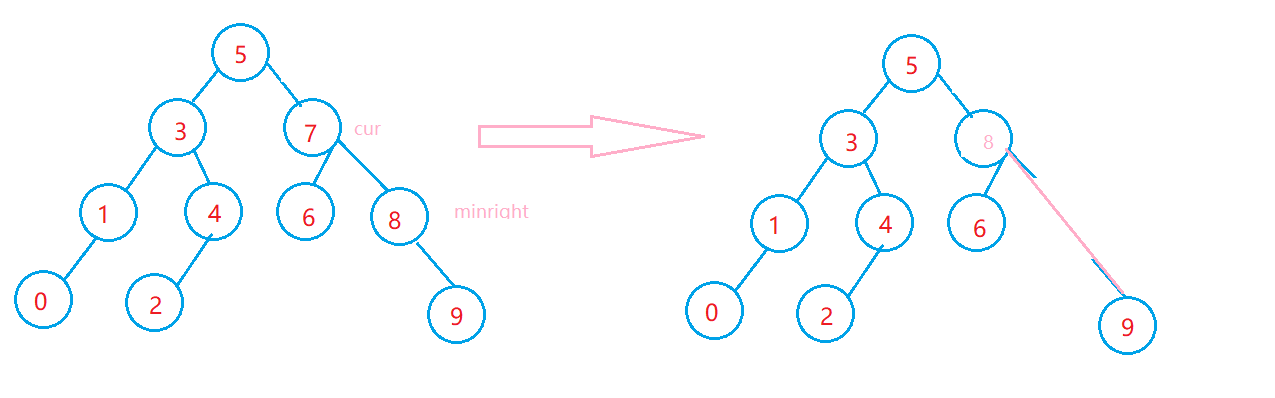
Non recursive version:
Note that only when the left subtree is empty or the right subtree is empty, the father is empty.
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
//For deep and shallow copies, the copy structure operator = needs to be implemented
bool Insert(const K& key)
{
if( _root == nullptr )
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while( cur )
{
if( cur->_key < key )
{
parent = cur;
cur = cur->_right;
}
else if( cur ->_key > key )
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(key);
if( parent ->_key < key )
{
parent ->_right = cur;
}
else parent ->_left = cur;
return true;
}
Node* Find(const K& key)
{
Node* cur =_root;
while(cur){
if( key >cur -> _key ) cur = cur -> _right;
else if( key < cur-> _key) cur = cur ->_left;
else return cur;
}
return nullptr;
}
void _InOrder(Node* root){
if(root == nullptr) return;
_InOrder(root->_left);
cout<<root->_key<<endl;
_InOrder(root->_right);
}
bool Erase(const K& key){
Node* parent = nullptr;
Node* cur = _root;
while( cur )
{
if( cur -> _key <key)
{
parent = cur;
cur =cur ->_right;
}
else if(cur -> _key > key)
{
parent =cur ;
cur =cur ->_left;
}
else{
//Found, ready to delete
//Left blank or right blank, give the other child to the father
if(_cur->_left == nullptr)
{
if( _cur == _root){
_root = _cur ->_right;
}
else{
if( parent ->_left ==cur)
{
parent->_left = cur ->_right;
}
else{
parent ->_right =cur ->_right;
}
delete _cur;
}
else if(_cur -->_right == nullptr)
{
if( _cur == _root){
_root = _cur -> _left;
}
else{
if( parent -> _left == cur)
{
parent ->_left =cur ->_left;
}
else{
parent ->_right=cur->_left;
}
}
delete _cur;
}
else{//The left and right are not empty, and the replacement method is used to delete
//Suppose that the minimum node of the right subtree is specified to replace
Node* minParent = cur;
Node* minRight = cur -> _right;
while(minRight -> _left) {minParent = minRight;minRight = minRight ->_left;}
cur->_key = minRight ->_key;//Save the value of the replacement node
//Delete replaced node
if(minParent -> _left == minRight){
minParent ->_left =minRight ->_right;
}
else minParent ->_right = minRight ->_right;
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root;
};
Recursive version of feature 3:
else{//The left and right are not empty, and the replacement method is used to delete
//Suppose that the minimum node of the right subtree is specified to replace
Node* minRight = cur -> _right;
while(minRight -> _left) minRight = minRight ->_left;
K mi =minRight ->_key;
//If you recursively call yourself to delete the replacement node, you will go to the case where the left is empty
this->Erase(mi);
cur->_key=mi;
}
#include"BinarySearchTree.h"
int main()
{
BSTree<int>t;
int a[]={5,3,4,1,7,8,2,6,0,9};
for(auto e :a)
{
t.Insert(e);
}
t.InOrder();
t.Erase(8);
t.InOrder();
t.Erase(5);
t.InOrder();
for(auto e: a){
t.Erase(e);
t.Inorder();
}
return 0;
}
Recursive version
In general, the recursive version sets another layer for the simplicity of the interface, so that the external call is more consistent with the encapsulation.
If you don't want to clear the details of the recursive version, draw the function recursive expansion diagram.
lookup
_ FindR lookup:
private:
Node* _FindR(Node* root , const K& key)
{
if(root == nullptr ) return nullptr;
if(root -> _key < key) return _FindR(root-> _right ,key);
else if( root-> _key > key) return _FindR(root -> _left ,key);
else return root;
}
public:
Node* FindR(const K& key){
return _FindR( _root,key);
}
insert
Is there any way to link the inserted node with the father?
- One way is to add a parent to the function parameter
- Or use Find to Find the father when it reaches the recursive boundary
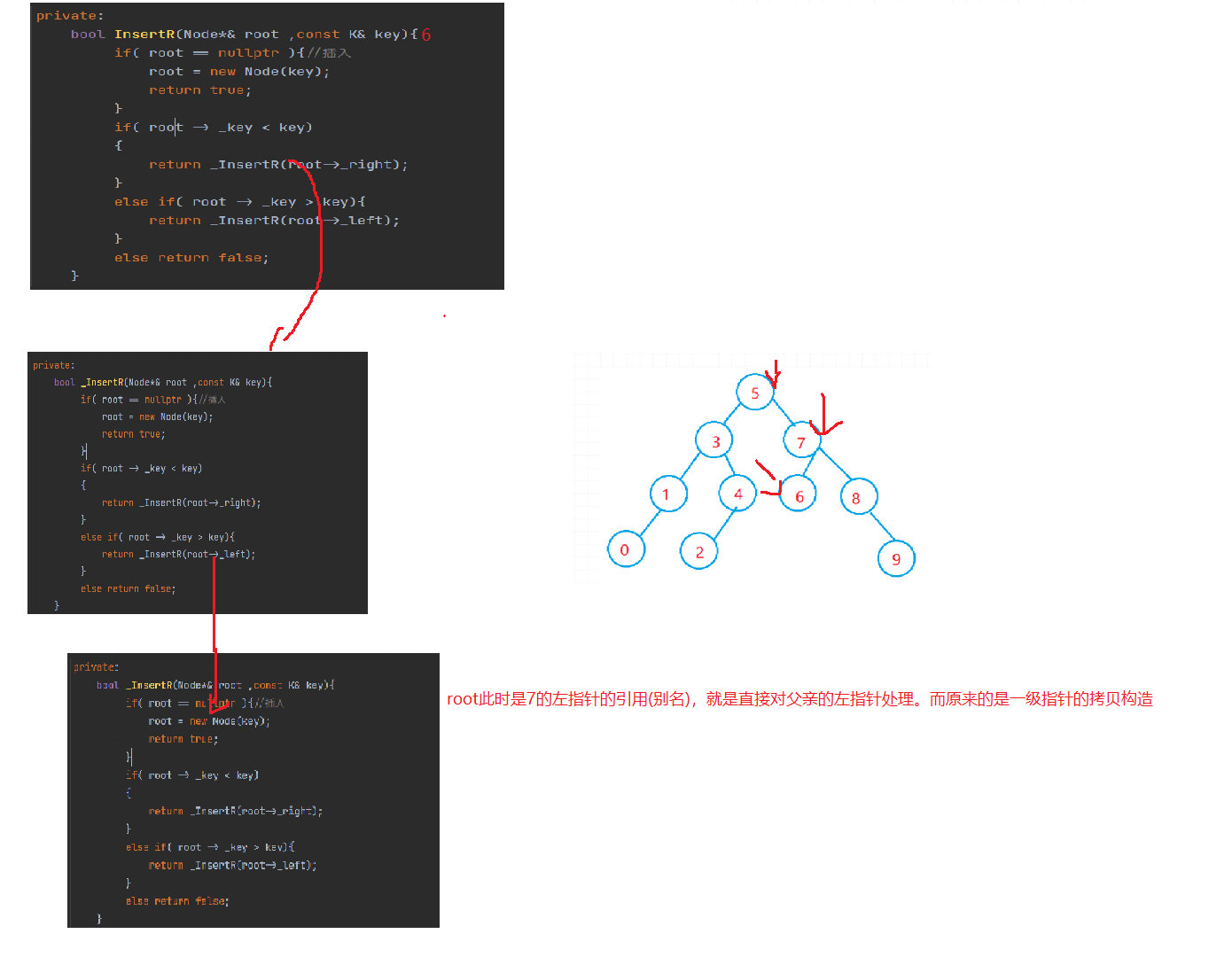
- Change the Node* root in the parameter to a reference (better)
private:
bool _InsertR(Node*& root ,const K& key){
if( root == nullptr ){//insert
root = new Node(key);
return true;
}
if( root -> _key < key)
{
return _InsertR(root->_right);
}
else if( root -> _key > key){
return _InsertR(root->_left);
}
else return false;
}
public:
bool InsertR( const K& key){
return _InsertR(_root,key);
}
delete
Recursive version:
For feature 3, recursion can find the case of feature 1 / 2, use their processing methods, and then assign values.
Because the reference is passed, the function parameters are not copied, so they want to be modified directly on the original drawing.
For feature 3, references do not work. One approach is to use the naive approach of feature 3 in the non recursive version.
private:
bool _EraseR(Node* &root,const K& key)
{
if( root ==nullptr ) return false;
if( root-> _key < key){
return _EraseR( root->_right,key);
}
else if( root -> _key > key){
return _EraseR( root-> _left,key);
}
else {
//Feature 1 and feature 2
if(root ->_left==nullptr )
{
Node* tmp = root;
root = root -> _right;
delete tmp;
return true;
}
else if(root ->_right == nullptr)
{
Node* tmp =root;
root = root ->_left;
delete tmp;
return true;
}
//Feature 3
else{
Node* minParent = root;
Node* minRight = root -> _right;
while(minRight -> _left) {minParent = minRight;minRight = minRight ->_left;}
root->_key = minRight ->_key;//Save the value of the replacement node
//Delete replaced node
if(minParent -> _left == minRight){
minParent ->_left =minRight ->_right;
}
else minParent ->_right = minRight ->_right;
delete minRight;
}
return true;
}
}
public:
bool EraseR(const K&key){
return _EraseR(root,key);
}
Another way is to use recursive processing of feature 3 in non recursion.
private:
bool _EraseR(Node* &root,const K& key)
{
if( root ==nullptr ) return false;
if( root-> _key < key){
return _EraseR( root->_right,key);
}
else if( root -> _key > key){
return _EraseR( root-> _left,key);
}
else {
//Feature 1 and feature 2
if(root ->_left==nullptr )
{
Node* tmp = root;
root = root -> _right;
delete tmp;
return true;
}
else if(root ->_right == nullptr)
{
Node* tmp =root;
root = root ->_left;
delete tmp;
return true;
}
//Feature 3
else{
Node* MinRight = root ->_right;
while(MinRight ->_left) MinRight= MinRight->_left;
K min = MinRight-> _key;
//Convert to delete Min in the right subtree of root
_EraseR(root->right,min);
root-> _key =min;
}
return true;
}
}
public:
bool EraseR(const K&key){
return _EraseR(root,key);
}
Default member function of class
Deconstruction
#include<iostream>
#include<string>
using namespace std;
template <typename K>
struct BSTreeNode
{
public:
BSTreeNode* _left;
BSTreeNode* _right;
BSTreeNode(K key)
:_left(nullptr),
_right(nullptr),
_key(key)
{ }
K _key;
};
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
~BSTree(){
_Destroy(_root);
_root=nullptr;
}
private:
void _Destroy(Node* root){
if(root == nullptr) return;
if(root->_left ) _Destroy(root->_left);
if(root->_right) _Destroy(root->_right);
delete root;
}
private:
Node* _root;
};
copy construction
First copy the root, then the left subtree, and then the right subtree.
#include<iostream>
#include<string>
using namespace std;
template <typename K>
struct BSTreeNode
{
public:
BSTreeNode* _left;
BSTreeNode* _right;
BSTreeNode(K key)
:_left(nullptr),
_right(nullptr),
_key(key)
{ }
K _key;
};
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
~BSTree(){
_Destroy(_root);
_root=nullptr;
}
BSTree(const BSTree<K>& t){
_root = _Copy(t._root);
}
private:
void _Destroy(Node* root){
if(root == nullptr) return;
if(root->_left ) _Destroy(root->_left);
if(root->_right) _Destroy(root->_right);
delete root;
}
Node* _Copy(Node* root){
if(root == nullptr) return nullptr;
Node* newnode = new Node(root ->_key);
newnode->_left = _Copy( root ->_left);
newnode->_right = _Copy(root -> _right);
return newnode;
}
private:
Node* _root;
};
operator = assignment
It is suggested that the assignment of operator = should be written in a modern way with the help of copy construction.
#include<iostream>
#include<string>
using namespace std;
template <typename K>
struct BSTreeNode
{
public:
BSTreeNode* _left;
BSTreeNode* _right;
BSTreeNode(K key)
:_left(nullptr),
_right(nullptr),
_key(key)
{ }
K _key;
};
template <typename K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
~BSTree(){
_Destroy(_root);
_root=nullptr;
}
BSTree(const BSTree<K>& t){
_root = _Copy(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root,t._root);
return *this;
}
private:
void _Destroy(Node* root){
if(root == nullptr) return;
if(root->_left ) _Destroy(root->_left);
if(root->_right) _Destroy(root->_right);
delete root;
}
Node* _Copy(Node* root){
if(root == nullptr) return nullptr;
Node* newnode = new Node(root ->_key);
newnode->_left = _Copy( root ->_left);
newnode->_right = _Copy(root -> _right);
return newnode;
}
private:
Node* _root;
};
Application of binary search tree
K model
K model: in the K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched.
The judgment of whether to find is the K model
Key search scenario: entrance guard of dormitory building, scanning and pole lifting system of garage, etc.
For example, for the entrance guard of the dormitory building, the student numbers of the students in the dormitory building can be stored in bstree < string > stunumset
For example, the scanning pole lifting system of the garage records the license plate number of the community owner into the system and puts it into bstree < string > carnumset
The code of the above implementation is the of the K model.
KV model
KV-(key-value)
KV search scenario:
- High speed railway station, buy tickets online, brush ID card to enter the station. Each ticket bought is associated with a person's ID number. The ID number is ID number. The ID number is read by the machine. The identity card number is found by the system. The date and the information of the ticket are read.
- Simple Chinese English Dictionary
- Count the number of occurrences of each word in a text
#include<iostream>
#include<string>
using namespace std;
namespace KV
{
template <typename K,typename V>
struct BSTreeNode
{
public:
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
BSTreeNode(const K& key,const V& value)
:_left(nullptr),
_right(nullptr),
_key(key),
_value(value)
{ }
K _key;
V _value;
};
template <typename K,typename V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
public:
BSTree()
:_root(nullptr)
{ }
//For deep and shallow copies, the copy structure operator = needs to be implemented
~BSTree(){
_Destroy(_root);
_root=nullptr;
}
BSTree(const BSTree<K>& t){
_root = _Copy(t._root);
}
BSTree<K, V>& operator=(BSTree<K, V> t)
{
swap(_root, t._root);
return *this;
}
public:
bool EraseR(const K&key){
return _EraseR(root,key);
}
bool InsertR( const K& key,const V&value){
return _InsertR(_root,key,value);
}
Node* FindR(const K& key){
return _FindR( _root,key);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
bool _InsertR(Node*& root ,const K& key,const V& value){
if( root == nullptr ){//insert
root = new Node(key,value);
return true;
}
if( root -> _key < key)
{
return _InsertR(root->_right);
}
else if( root -> _key > key){
return _InsertR(root->_left);
}
else return false;
}
Node* _FindR(Node* root , const K& key)
{
if(root == nullptr ) return nullptr;
if(root -> _key < key) return _FindR(root-> _right ,key);
else if( root-> _key > key) return _FindR(root -> _left ,key);
else return root;
}
bool _EraseR(Node* &root,const K& key)
{
if( root ==nullptr ) return false;
if( root-> _key < key){
return _EraseR( root->_right,key);
}
else if( root -> _key > key){
return _EraseR( root-> _left,key);
}
else {
//Feature 1 and feature 2
if(root ->_left==nullptr )
{
Node* tmp = root;
root = root -> _right;
delete tmp;
return true;
}
else if(root ->_right == nullptr)
{
Node* tmp =root;
root = root ->_left;
delete tmp;
return true;
}
//Feature 3
else{
Node* MinRight = root ->_right;
while(MinRight ->_left) MinRight= MinRight->_left;
K min = MinRight-> _key;
V value = MinRight->_value;
//Convert to delete Min in the right subtree of root
_EraseR(root->right,min);
root-> _key =min;
root->_value = value;
}
return true;
}
}
void _Destory(Node* root)
{
if (root == NULL)
{
return;
}
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
Node* _Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* copyNode = new Node(root->_key, root->_value);
copyNode->_left = _Copy(root->_left);
copyNode->_right = _Copy(root->_right);
return copyNode;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":"<<root->_value<<endl;
_InOrder(root->_right);
}
private:
Node* _root;
};
}
Simply test an example of a simple dictionary
void TestBSTree()
{
KV::BSTree<string,string> dict;
dict.InsertR("apple","Apple");
dict.InsertR("banana","Banana");
dict.InsertR("candy","candy");
dict.InsertR("duck","duck");
string str;
while(cin>>str){
KV: : BSTreeNode<string,string> *ret = dict.FindR(str);
if(ret == nullptr) {
cout<<"Misspelled words"<<endl;
}
else{
cout<<string<<" Chinese Translation "<<ret->_value<<endl;
}
}
}
Test the example of counting the number of words
void TestBSTree()
{
string arr[]={"aaa","bb","cc","cc","bb","aaa","aaa","aaa","d"};
KV::BSTree<string,int> countTree;
for(const auto& str:arr)
{
//Find the search tree first
//No instructions to insert
auto ret = countTree.FindR(str);
if(ret == nullptr){
coutTree.InsertR(str,1);
}
else{
ret->value ++;
}
}
}