1, Key analysis
1. Insert node
Inserting a node is relatively simple. You only need to judge the key value, replace the corresponding key value, or create a new key value.
// Insert the node (key, value) into the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the binary search tree after inserting a new node
Node* insert(Node *node, Key key, Value value){
if( node == NULL ){
count ++;
return new Node(key, value);
}
if( key == node->key )
node->value = value;
else if( key < node->key )
node->left = insert( node->left , key, value);
else // key > node->key
node->right = insert( node->right, key, value);
return node;
}
2. Delete node
2.1. Delete the latest value
First, the minimum value of BST will only have a right subtree. Similarly, the maximum value of BST will only have left subtree.
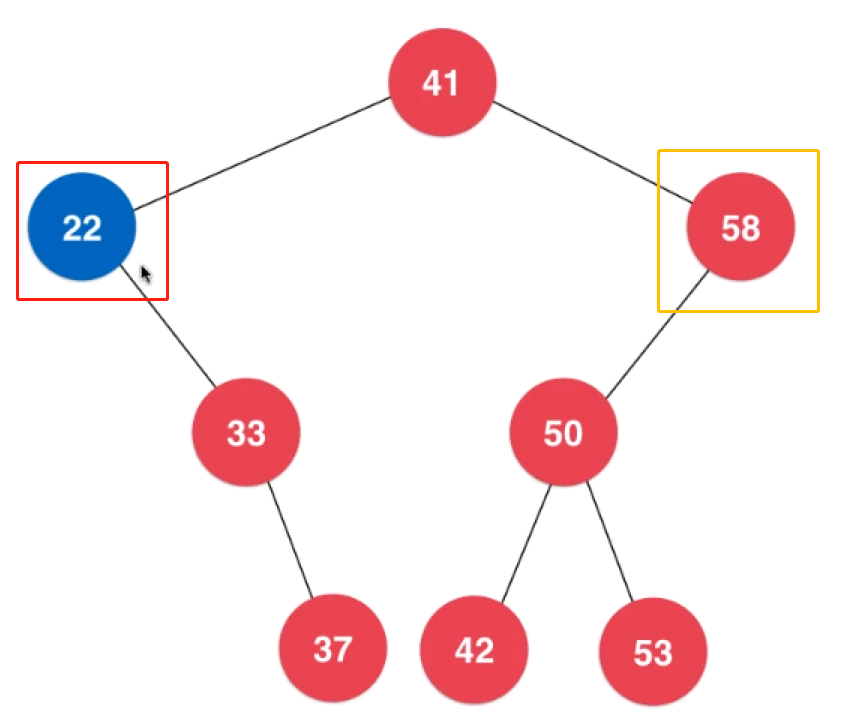
Delete minimum value: just find the minimum value to the left, link its right subtree to the parent node of the minimum value, and then delete the minimum value.
Delete maximum value: just find the maximum value to the right, link its left sub tree to the parent node of the maximum value, and then delete the maximum value.
Similarly, if the right subtree is empty, there is no problem connecting it.
// Delete the smallest node in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* removeMin(Node* node){
if( node->left == NULL ){
Node* rightNode = node->right;
delete node;
count --;
return rightNode;
}
node->left = removeMin(node->left);
return node;
}
// Delete the largest node in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* removeMax(Node* node){
if( node->right == NULL ){
Node* leftNode = node->left;
delete node;
count --;
return leftNode;
}
node->right = removeMax(node->right);
return node;
}
2.2. Delete general nodes
Deleting a general node is divided into several categories
- The node to be deleted has only the right child.
- Only the left child is the node to be deleted.
- There are children on both sides of the deleted node.
For the above three cases, only the last one is slightly complicated.
- Link its right child to its parent node and delete the node
- Link its left child to its parent node and delete the node
- Change the successor node of this node to the current node and delete the location of the original successor node. (the successor node replaces the node position)
The successor node is the smallest node in the right subtree of the node.
Of course, this operation can also be completed with the preamble node.
The preceding node is the largest node in the left subtree of this node (see node 53 in the figure below).
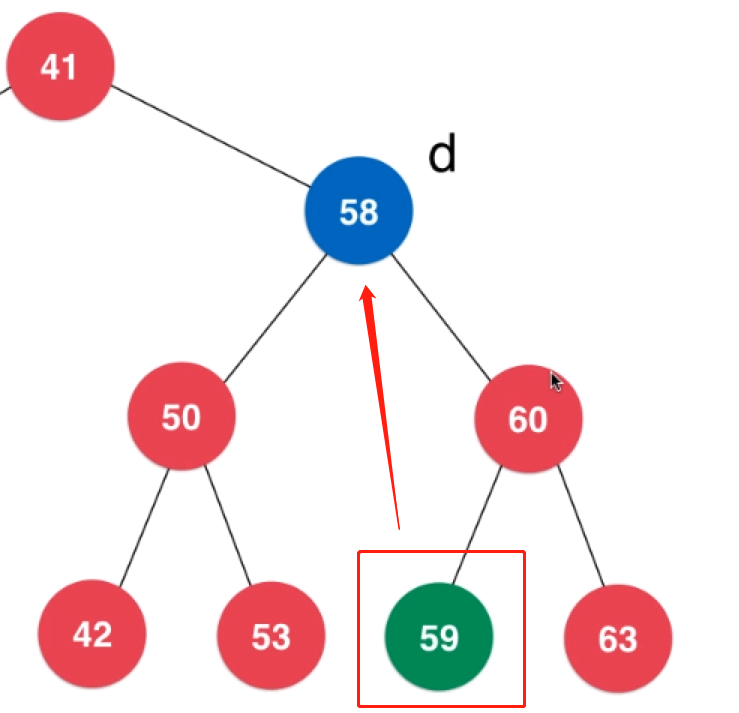
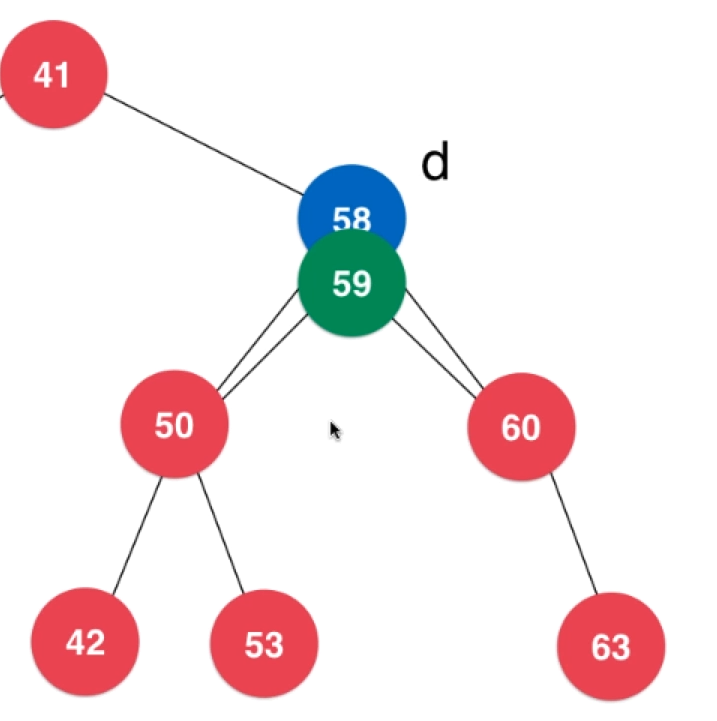
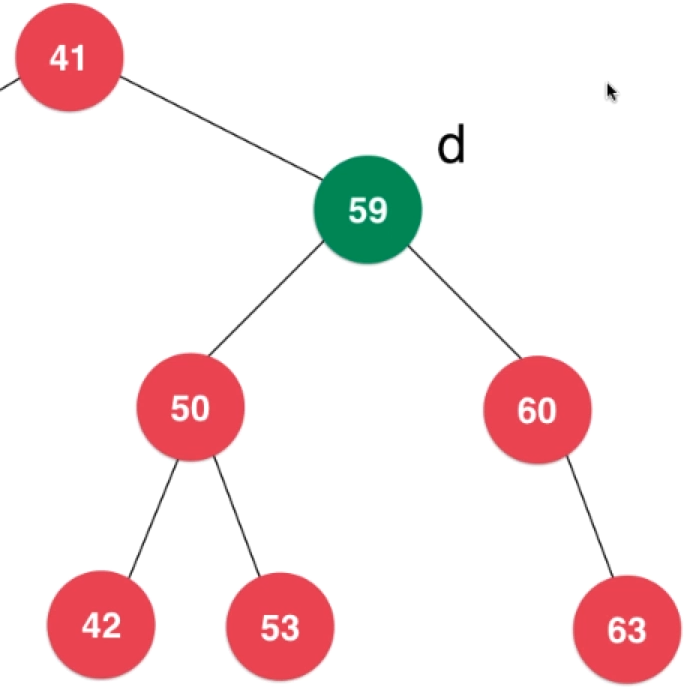
// Delete the node with the key value as the key in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* remove(Node* node, Key key){
if( node == NULL )
return NULL;
if( key < node->key ){
node->left = remove( node->left , key );
return node;
}
else if( key > node->key ){
node->right = remove( node->right, key );
return node;
}
else{ // key == node->key
if( node->left == NULL ){
Node *rightNode = node->right;
delete node;
count --;
return rightNode;
}
if( node->right == NULL ){
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
// node->left != NULL && node->right != NULL
Node *successor = new Node(minimum(node->right));
count ++;
successor->right = removeMin(node->right);
successor->left = node->left;
delete node;
count --;
return successor;
}
}
3. Destructor
Destructor requires the idea of post order traversal.
That is, to delete the current node, the left and right subtrees must be deleted first, otherwise the whole tree cannot be deleted.
The following code is actually a recursive destructor of post order traversal.
// Release all nodes of the binary search tree with node as the root
// Recursive algorithm with subsequent traversal
void destroy(Node* node){
if( node != NULL ){
destroy( node->left );
destroy( node->right );
delete node;
count --;
}
}
2, Complete BST class
The complete code is taken from Mr. bobo's github, and there is a path at the end of the text.
// Binary search tree
template <typename Key, typename Value>
class BST{
private:
// The nodes in the tree are private structures, and the outside world does not need to know the specific implementation of binary search tree nodes
struct Node{
Key key;
Value value;
Node *left;
Node *right;
Node(Key key, Value value){
this->key = key;
this->value = value;
this->left = this->right = NULL;
}
Node(Node *node){
this->key = node->key;
this->value = node->value;
this->left = node->left;
this->right = node->right;
}
};
Node *root; // Root node
int count; // Number of nodes in the tree
public:
// Constructor, which constructs an empty binary search tree by default
BST(){
root = NULL;
count = 0;
}
// Destructor to release all space of binary search tree
~BST(){
destroy( root );
}
// Returns the number of nodes in the binary search tree
int size(){
return count;
}
// Returns whether the binary search tree is empty
bool isEmpty(){
return count == 0;
}
// Insert a new (key, value) data pair into the binary search tree
void insert(Key key, Value value){
root = insert(root, key, value);
}
// Check whether the key exists in the binary search tree
bool contain(Key key){
return contain(root, key);
}
// Search the value corresponding to the key in the binary search tree. If this value does not exist, NULL is returned
Value* search(Key key){
return search( root , key );
}
// Preorder traversal of binary search tree
void preOrder(){
preOrder(root);
}
// Middle order traversal of binary search tree
void inOrder(){
inOrder(root);
}
// Post order traversal of binary search tree
void postOrder(){
postOrder(root);
}
// Sequence traversal of binary search tree
void levelOrder(){
queue<Node*> q;
q.push(root);
while( !q.empty() ){
Node *node = q.front();
q.pop();
cout<<node->key<<endl;
if( node->left )
q.push( node->left );
if( node->right )
q.push( node->right );
}
}
// Find the minimum key value of binary search tree
Key minimum(){
assert( count != 0 );
Node* minNode = minimum( root );
return minNode->key;
}
// Find the maximum key value of the binary search tree
Key maximum(){
assert( count != 0 );
Node* maxNode = maximum(root);
return maxNode->key;
}
// Delete the node with the minimum value from the binary search tree
void removeMin(){
if( root )
root = removeMin( root );
}
// Delete the node with the maximum value from the binary search tree
void removeMax(){
if( root )
root = removeMax( root );
}
// Delete key from search tree
void remove(Key key){
root = remove(root, key);
}
private:
// Insert the node (key, value) into the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the binary search tree after inserting a new node
Node* insert(Node *node, Key key, Value value){
if( node == NULL ){
count ++;
return new Node(key, value);
}
if( key == node->key )
node->value = value;
else if( key < node->key )
node->left = insert( node->left , key, value);
else // key > node->key
node->right = insert( node->right, key, value);
return node;
}
// Check whether the binary search tree with node as the root contains nodes with key value, and use recursive algorithm
bool contain(Node* node, Key key){
if( node == NULL )
return false;
if( key == node->key )
return true;
else if( key < node->key )
return contain( node->left , key );
else // key > node->key
return contain( node->right , key );
}
// Find the value corresponding to the key in the binary search tree with node as the root, and use the recursive algorithm
// If value does not exist, NULL is returned
Value* search(Node* node, Key key){
if( node == NULL )
return NULL;
if( key == node->key )
return &(node->value);
else if( key < node->key )
return search( node->left , key );
else // key > node->key
return search( node->right, key );
}
// The binary search tree with node as the root is traversed in advance, and the recursive algorithm
void preOrder(Node* node){
if( node != NULL ){
cout<<node->key<<endl;
preOrder(node->left);
preOrder(node->right);
}
}
// The binary search tree with node as the root is traversed in middle order, and the recursive algorithm
void inOrder(Node* node){
if( node != NULL ){
inOrder(node->left);
cout<<node->key<<endl;
inOrder(node->right);
}
}
// The binary search tree with node as the root is traversed in order, and the recursive algorithm is used
void postOrder(Node* node){
if( node != NULL ){
postOrder(node->left);
postOrder(node->right);
cout<<node->key<<endl;
}
}
// Release all nodes of the binary search tree with node as the root
// Recursive algorithm with subsequent traversal
void destroy(Node* node){
if( node != NULL ){
destroy( node->left );
destroy( node->right );
delete node;
count --;
}
}
// Returns the node where the minimum key value of the binary search tree with node as the root is located, and the recursive algorithm
Node* minimum(Node* node){
if( node->left == NULL )
return node;
return minimum(node->left);
}
// Returns the node where the maximum key value of the binary search tree with node as the root is located, and the recursive algorithm
Node* maximum(Node* node){
if( node->right == NULL )
return node;
return maximum(node->right);
}
// Delete the smallest node in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* removeMin(Node* node){
if( node->left == NULL ){
Node* rightNode = node->right;
delete node;
count --;
return rightNode;
}
node->left = removeMin(node->left);
return node;
}
// Delete the largest node in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* removeMax(Node* node){
if( node->right == NULL ){
Node* leftNode = node->left;
delete node;
count --;
return leftNode;
}
node->right = removeMax(node->right);
return node;
}
// Delete the node with the key value as the key in the binary search tree with node as the root, and use the recursive algorithm
// Returns the root of the new binary search tree after deleting the node
Node* remove(Node* node, Key key){
if( node == NULL )
return NULL;
if( key < node->key ){
node->left = remove( node->left , key );
return node;
}
else if( key > node->key ){
node->right = remove( node->right, key );
return node;
}
else{ // key == node->key
if( node->left == NULL ){
Node *rightNode = node->right;
delete node;
count --;
return rightNode;
}
if( node->right == NULL ){
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
// node->left != NULL && node->right != NULL
Node *successor = new Node(minimum(node->right));
count ++;
successor->right = removeMin(node->right);
successor->left = node->left;
delete node;
count --;
return successor;
}
}
};