1. Bubble sorting
Bubble Sort is A simple sorting algorithm. It repeatedly visits the sequence to be sorted, compares two elements at A time, and exchanges them if their order (such as from small to large and the initials A to Z) is wrong.
Process demonstration:

example:
#include <stdio.h> void bubble_sort(int arr[], int len) { int i, j, temp; for (i = 0; i < len - 1; i++) for (j = 0; j < len - 1 - i; j++) if (arr[j] > arr[j + 1]) { temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } int main() { int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 }; int len = (int) sizeof(arr) / sizeof(*arr); bubble_sort(arr, len); int i; for (i = 0; i < len; i++) printf("%d ", arr[i]); return 0; }
Select sort
Selection sort is a simple and intuitive sorting algorithm. Its working principle is as follows: first, find the smallest (large) element in the last sorting sequence and store it at the beginning of the sorting sequence, and then continue to find the smallest (large) element from the remaining unordered elements Element, and then put it at the end of the sorted. And so on until all elements are sorted.
Demonstration process:

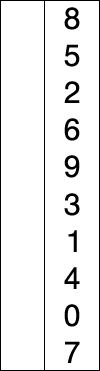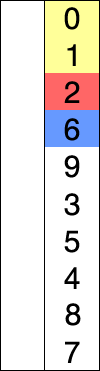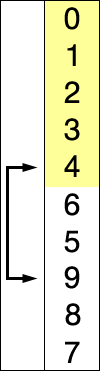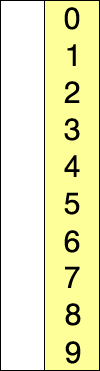
example:
void selection_sort(int a[], int len) { int i,j,temp; for (i = 0 ; i < len - 1 ; i++) { int min = i; // Record the minimum value, and the first element defaults to the minimum value for (j = i + 1; j < len; j++) // Access unordered elements { if (a[j] < a[min]) // Find current minimum { min = j; // Record minimum } } if(min != i) { temp=a[min]; // Swap two variables a[min]=a[i]; a[i]=temp; } /* swap(&a[min], &a[i]); */ // Use custom function exchange } } /* void swap(int *a,int *b) // Swap two variables { int temp = *a; *a = *b; *b = temp; } */
2. Insert sorting
Insert sort (English: Insertion Sort) is a simple and intuitive sorting algorithm. Its working principle is to construct an ordered sequence. For unordered data, scan forward in the sorted sequence, find the corresponding position and insert. Insertion sorting is usually implemented by in place sorting. Therefore, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements backward step by step To provide insertion space for the latest elements.
Process demonstration:

example
void insertion_sort(int arr[], int len){ int i,j,temp; for (i=1;i<len;i++){ temp = arr[i]; for (j=i;j>0 && arr[j-1]>temp;j--) arr[j] = arr[j-1]; arr[j] = temp; } }
3. Hill sort
Hill sort, also known as decreasing incremental sort algorithm, is a more efficient improved version of insertion sort. Hill sort is a stable sort algorithm. Hill sort proposes an improved method based on the following two properties of insertion sort:
- Insertion sorting is efficient when operating on almost ordered data, that is, it can achieve the efficiency of linear sorting
- But insert sort is generally inefficient because insert sort can only move data one bit at a time
Process demonstration:
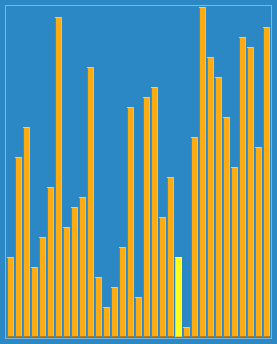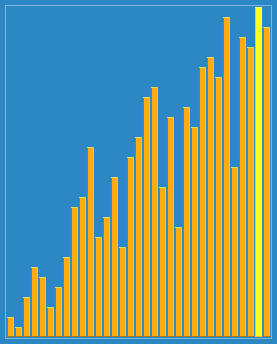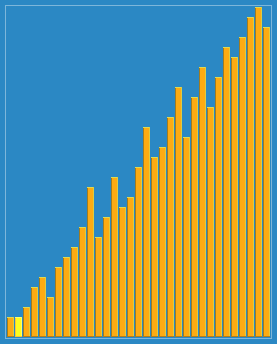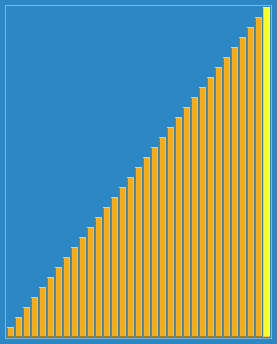
example
void shell_sort(int arr[], int len) { int gap, i, j; int temp; for (gap = len >> 1; gap > 0; gap = gap >> 1) for (i = gap; i < len; i++) { temp = arr[i]; for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) arr[j + gap] = arr[j]; arr[j + gap] = temp; } }
4. Merge and sort
Divide the data into two segments, select the smallest element one by one from the two segments and move it to the end of the new data segment.
It can be done from top to bottom or from bottom to top.
Process demonstration:

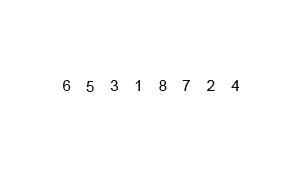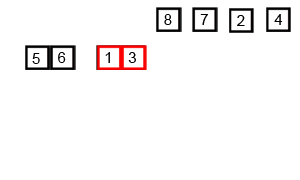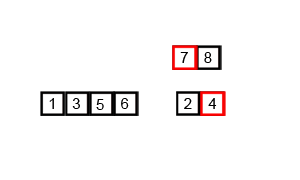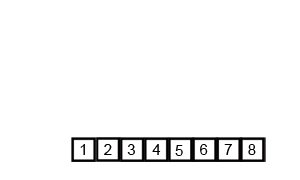
Iterative method
int min(int x, int y) { return x < y ? x : y; } void merge_sort(int arr[], int len) { int* a = arr; int* b = (int*) malloc(len * sizeof(int)); int seg, start; for (seg = 1; seg < len; seg += seg) { for (start = 0; start < len; start += seg + seg) { int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len); int k = low; int start1 = low, end1 = mid; int start2 = mid, end2 = high; while (start1 < end1 && start2 < end2) b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++]; while (start1 < end1) b[k++] = a[start1++]; while (start2 < end2) b[k++] = a[start2++]; } int* temp = a; a = b; b = temp; } if (a != arr) { int i; for (i = 0; i < len; i++) b[i] = a[i]; b = a; } free(b); }
Recursive method
1 void merge_sort_recursive(int arr[], int reg[], int start, int end) { 2 if (start >= end) 3 return; 4 int len = end - start, mid = (len >> 1) + start; 5 int start1 = start, end1 = mid; 6 int start2 = mid + 1, end2 = end; 7 merge_sort_recursive(arr, reg, start1, end1); 8 merge_sort_recursive(arr, reg, start2, end2); 9 int k = start; 10 while (start1 <= end1 && start2 <= end2) 11 reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++]; 12 while (start1 <= end1) 13 reg[k++] = arr[start1++]; 14 while (start2 <= end2) 15 reg[k++] = arr[start2++]; 16 for (k = start; k <= end; k++) 17 arr[k] = reg[k]; 18 } 19 void merge_sort(int arr[], const int len) { 20 int reg[len]; 21 merge_sort_recursive(arr, reg, 0, len - 1); 22 }
5. Quick sort
Randomly select an element in the interval as the benchmark, put the element less than the benchmark before the benchmark, and the element greater than the benchmark after the benchmark, and then sort the decimal area and large number area respectively.
Process demonstration:
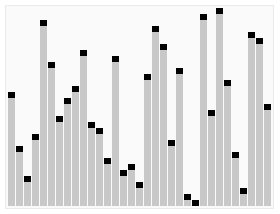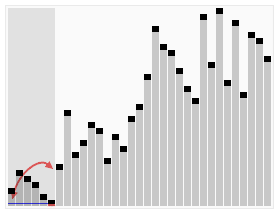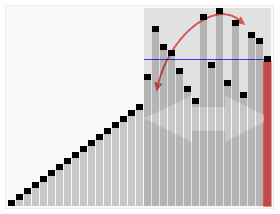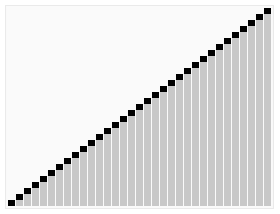
Iterative method
1 typedef struct _Range { 2 int start, end; 3 } Range; 4 Range new_Range(int s, int e) { 5 Range r; 6 r.start = s; 7 r.end = e; 8 return r; 9 } 10 void swap(int *x, int *y) { 11 int t = *x; 12 *x = *y; 13 *y = t; 14 } 15 void quick_sort(int arr[], const int len) { 16 if (len <= 0) 17 return; // avoid len A segment error is raised when the value is equal to a negative value( Segment Fault) 18 // r[]Simulation list,p For quantity,r[p++]For push,r[--p]For pop And get the element 19 Range r[len]; 20 int p = 0; 21 r[p++] = new_Range(0, len - 1); 22 while (p) { 23 Range range = r[--p]; 24 if (range.start >= range.end) 25 continue; 26 int mid = arr[(range.start + range.end) / 2]; // Select the middle point as the datum point 27 int left = range.start, right = range.end; 28 do 29 { 30 while (arr[left] < mid) ++left; // Check whether the left side of the reference point meets the requirements 31 while (arr[right] > mid) --right; //Check whether the right side of the reference point meets the requirements 32 33 if (left <= right) 34 { 35 swap(&arr[left],&arr[right]); 36 left++;right--; // Move the pointer to continue 37 } 38 } while (left <= right); 39 40 if (range.start < right) r[p++] = new_Range(range.start, right); 41 if (range.end > left) r[p++] = new_Range(left, range.end); 42 } 43 }
Recursive method
1 void swap(int *x, int *y) { 2 int t = *x; 3 *x = *y; 4 *y = t; 5 } 6 void quick_sort_recursive(int arr[], int start, int end) { 7 if (start >= end) 8 return; 9 int mid = arr[end]; 10 int left = start, right = end - 1; 11 while (left < right) { 12 while (arr[left] < mid && left < right) 13 left++; 14 while (arr[right] >= mid && left < right) 15 right--; 16 swap(&arr[left], &arr[right]); 17 } 18 if (arr[left] >= arr[end]) 19 swap(&arr[left], &arr[end]); 20 else 21 left++; 22 if (left) 23 quick_sort_recursive(arr, start, left - 1); 24 quick_sort_recursive(arr, left + 1, end); 25 } 26 void quick_sort(int arr[], int len) { 27 quick_sort_recursive(arr, 0, len - 1); 28 }