⌛️

Chorus ☁️

Link to previous question: C/C + + 100 questions punch in [4 / 100] - maximum number of fusion ⭐ ️ ⭐ Test mathematics.
General contents of 100 punch outs: 🚧 🚧 …

1, Title Overview

n n n students stand in a row. The music teacher wants to invite one of them k k k students out of the line, making the rest n − k n-k n − k students lined up in chorus.

Chorus formation refers to: setting n n n students are numbered from left to right 1 , 2 , ... k , . . . , n 1,2, ... k,...,n 1,2,...k,...,n.
And their height is t 1 < t 2 < . . . < t k − 1 < t k > t k + 1 > . . . > t n t_1<t_2<...<t_{k-1}<t_k>t_{k+1}>...>t_n t1​<t2​<...<tk−1​<tk​>tk+1​>...>tn​
Note:“ t 1 < t 2 < . . . t n t_1<t_2<...t_n t1​<t2​<... TN "and“ t 1 > t 2 > . . . > t n t_1>t_2>...>t_n t1​>t2​>...> "TN" is also a chorus formation
Your task is to know all n n For the height of n students, at least a few students need to be listed to make the remaining students form a chorus formation.

● input Description:

Two lines in total.

The first line is an integer n n n( 2 ≤ n ≤ 100 2≤n≤100 2 ≤ n ≤ 100), indicating the total number of students.

The second line has n n n integers, separated by spaces, th i i i integers t i t_i ti​ ( 130 ≤ t i ≤ 230 130≤t_i≤230 130 ≤ ti ≤ 230) is the second i i Height of i students (CM).

● output Description:

An integer requires at least several students to list.

● note:

① Operation limit - > maximum operation time: 1 s 1s 1s, maximum running memory: 128 M 128M 128M； ② For 50 50% 50 data, guaranteed n ≤ 20 n≤20 n ≤ 20, for all data, it is guaranteed to have n ≤ 100 n≤100 n≤100.

  ● input example:

8
190 186 150 200 160 130 197 120

  ● output example:

3

● example explanation: one of the best ways to list is - > the first and second students and the penultimate students. The remaining five form a chorus.

2, Thinking blank

● topic difficulty: ⭐ ️ ⭐ ️ ⭐ ️ ⭐ ️

● suggested thinking time: ⌛ ️ ⌛ ️

3, Topic analysis

● this is a question to examine the array.

● I believe that after you get this question, the most intuitive feeling is to find a "small hill" based on height, and the longer it is, the better. As shown in the figure below

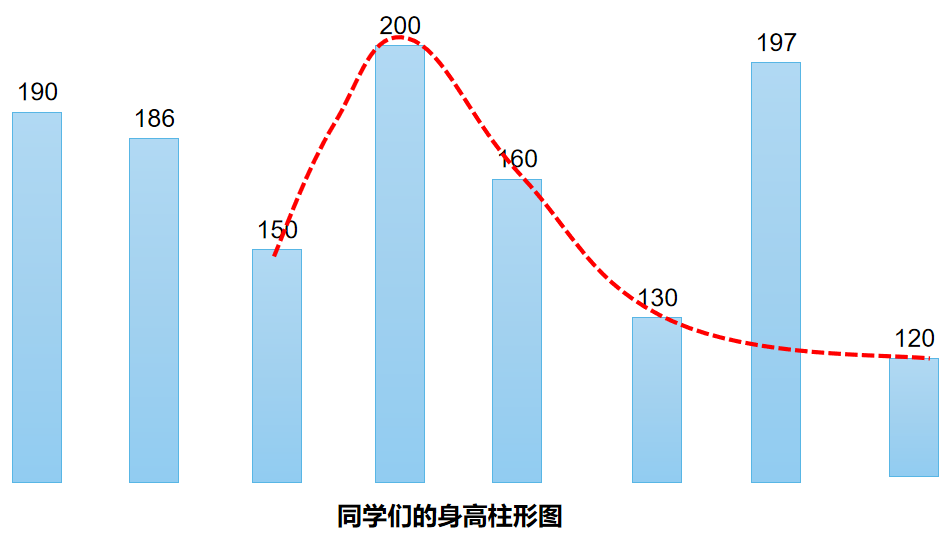
● how to design an algorithm to realize this function? That is, how to find the best "hill"?

● the simplest idea I came up with is to traverse each student from left to right, and when I traverse to the second k k When k students, Ta looks to the left to see the length of the "longest increment sequence" on the left l e n 1 len_1 len1, and then look to the right to see the length of the "longest subtraction sequence" on his right l e n 2 len_2 len2, so for Ta, if it is the "peak" of the chorus, the number of the chorus is l e n 1 + l e n 2 + 1 len_1 + len_2 + 1 len1​+len2​+1. Finally, we just have to pick out the largest number.

● but the question is, how to find the "length of the longest increment sequence"? (if you can find it, you won't have a problem finding the "longest subtraction sequence")
That is, for example, we require the length of the longest increment sequence of the sequence "4 1 2 1 3 5 17" (note that it is strictly increasing). Obviously, the length of "1 23 5 17" is, that is, the length of the longest increment sequence is 5, as shown in the figure below:

● you can still see this with your eyes, but if the array is very long, it won't look good? How do you calculate it? A simple and practical method is provided here:

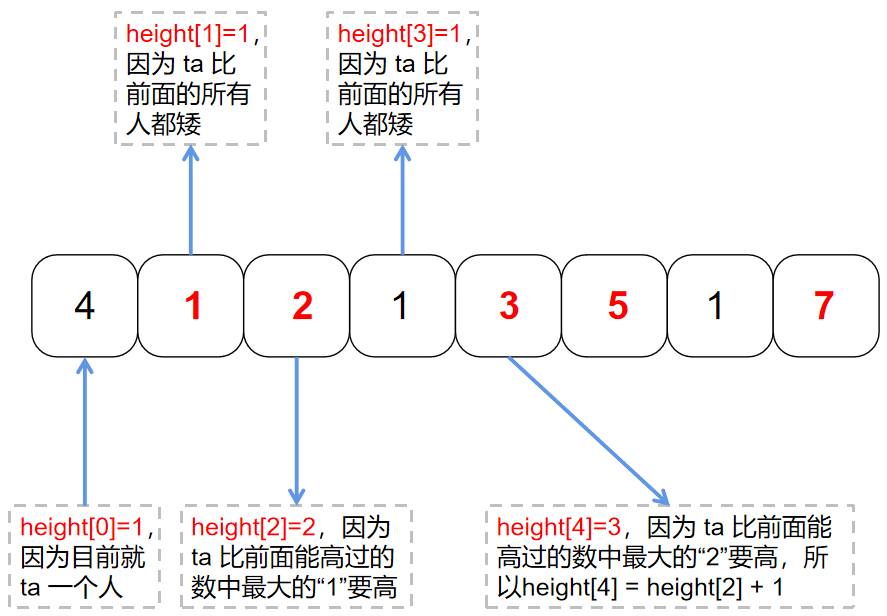
Use an array height [] to record the length of "the longest increment sequence from left to right with this student as the end point".
When you want to get height[k], find the subscript j ( And j < k ) J (and j < K) J (and j < K), and height[j] < height [k], and height[j] is the largest value of height in the subscript j < K
● the schematic diagram is as follows:

● well, since you can find the "length of the longest increasing sequence", then the "length of the longest decreasing sequence" can be solved easily (that is, you can find the length of the longest increasing sequence along the sequence in reverse).

● when I thought of this, I suddenly thought of traversing students one by one, and then traversing each student to refresh the height [] array. Although it is feasible, it seems that it can be simplified.

● after some thinking, when my left hand makes an uphill comparison and my right hand makes a downhill comparison, I suddenly think of a good method, that is, the next algorithm idea:

① First, the second i i i students as the end point, calculate the length of the longest subsequence from left to right (this student is the end point), and store them in h e i g h t 1 [ i ] height_1[i] In hight1 [i]
② Then take the second j j j students as the end point, calculate the length of the longest subsequence from right to left (this student is the end point), and store them in h e i g h t 2 [ j ] height_2[j] In high2 [j]
③ After traversing each student (assuming No k k k-bit), just find all h e i g h t 1 [ k ] + h e i g h t 2 [ k ] − 1 height_1[k] + height_2[k] - 1 The maximum number in hight1 [k] + hight2 [k] - 1 is the maximum number of people in the current chorus team
④ The question requires the minimum number of people to be calculated, so the answer = all the people - the maximum number of the current chorus team
● the schematic diagram is as follows:

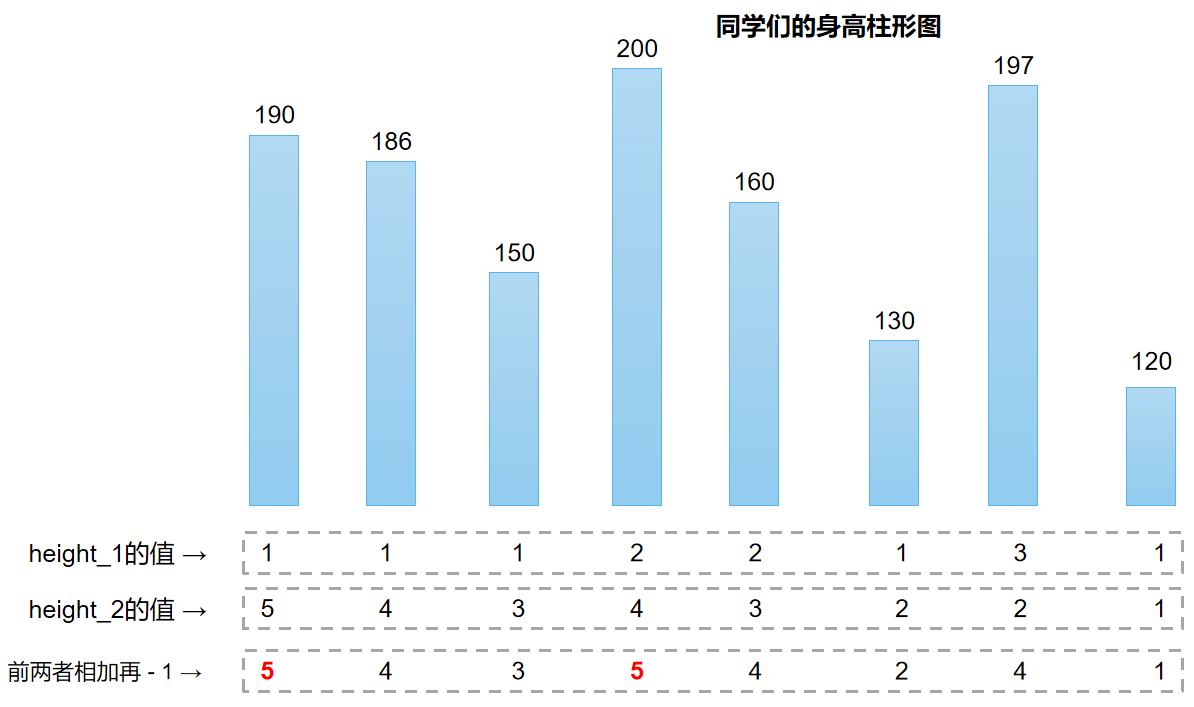
● Description: it can be found that there are actually two final answers (if according to the requirements of the question), as long as any one is considered.

● algorithm design:
[1] Design the input and output module.

[2] Design the longest subsequence initialization module:

[3] Design the maximum number module

Step [1]: I / O module

  ● this is relatively easy:

#include<stdio.h>
int main()
{
    /* Input module */
    int n;
    int a[110];     // According to the requirements of the topic, as long as the space is greater than 100
    int rev_a[110];	// rev is the abbreviation of "reverse" in the code world. We define this array for the convenience of height_2[]
    scanf("%d", &n);
    for (i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
        rev_a[ n-i-1 ] = a[i];	// rev_a [] is the reverse order of a [].
    }
    /* Longest subsequence initialization module */
    ...

    /* Maximum module */
    ...

    /* output module  */
    pritnf("%d", answer);
    return 0;
}

Step [2]: Longest subsequence initialization module

#include<stdio.h>
/*
* Function function: find out the length of the longest adder sequence including the sequence of the ith student and the previous student.
* Parameter Description:
* [1] arr[]: Height array
* [2] height[]: It's height_1 [] and height_ The "double" of 2 [] stores an array of subsequences
* [3] N: That is to traverse the subscript i of the ith student.
*/
int find(int arr[], int height[], int N)
{
    int best_num = -1;
    int cur_height = arr[N];
    for (int i = 0; i < N; i++)
    {
        if (arr[i] < cur_height)        // First of all, the height of one of the students in front is smaller than that of the i-th student
        {
            if (height[i] > best_num)   // Secondly, if the maximum subsequence value can be updated, it will be updated.
            {
                best_num = height[i];
            }
        }
    }
    if (best_num == -1) // If the value remains unchanged, it indicates that the i-th student is currently one of the shortest
        return 1;
    else
        return best_num + 1;    // Otherwise, a value of + 1 is returned
}

int main()
{
    /* Input module */
	...

    /* Longest subsequence initialization module */
    int height_1[110], height_2[110];
    for (int i = 0; i < n; i++)		// Initialize first
        height_1[i] = height_2[i] = 1;
    for (i = 0; i < n; i++)			// Then deal with it 
    {
        height_1[i] = find(a, height_1, i);
        height_2[i] = find(rev_a, height_2, i);
    }

    /* Maximum module */
	...

    /* output module  */
    ...
    return 0;
}

Step [3]: find the maximum number module

● this is a relatively simple point, that is, to find the maximum value in a group of numbers, but with a little more calculation.

/* Maximum module */
int max_num;
for (i = 0; i < n; i++)
{
    int j = n - i - 1;		// Note: our height_2 [] is based on rev_a [] calculated, 
    						// And rev_a [] is the reverse order of a [], so finally we have to reverse it
    if (max_num < height_1[i] + height_2[j] - 1)
    {
        max_num = height_1[i] + height_2[j] - 1;
    }
}

/* output module  */
pritnf("%d", n - max_num);		// Remember to reduce it at the end
return 0;

4, Summary and reflection

  ● to solve a problem, we often first consider how to solve it first, and then consider how to optimize it. The problem is.

  ● the method of reverse order + auxiliary array (height_1 [] and height_2 []) is combined to simplify the problem.

5, Complete code (C and C + +)

  ● C language version:

#include<stdio.h>

/*
* Function function: find out the length of the longest adder sequence including the sequence of the ith student and the previous student.
* Parameter Description:
* [1] arr[]: Height array
* [2] height[]: It's height_1 [] and height_ The "double" of 2 [] stores an array of subsequences
* [3] N: That is to traverse the subscript i of the ith student.
*/
int find(int arr[], int height[], int N)
{
    int best_num = -1;
    int cur_height = arr[N];
    for (int i = 0; i < N; i++)
    {
        if (arr[i] < cur_height)        // First of all, the height of one of the students in front is smaller than that of the i-th student
        {
            if (height[i] > best_num)   // Secondly, if the maximum subsequence value can be updated, it will be updated.
            {
                best_num = height[i];
            }
        }
    }
    if (best_num == -1) // If the value remains unchanged, it indicates that the i-th student is currently one of the shortest
        return 1;
    else
        return best_num + 1;    // Otherwise, a value of + 1 is returned
}

int main()
{
    /* Input module */
    int a[110], rev_a[110];
    int i, n;
    scanf("%d", &n);
    for (i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
        rev_a[n - i - 1] = a[i];
    }

    /* Longest subsequence initialization module*/
    int height_1[110], height_2[110];
    for (int i = 0; i < n; i++)
        height_1[i] = height_2[i] = 1;
    for (i = 0; i < n; i++)
    {
        height_1[i] = find(a, height_1, i);
        height_2[i] = find(rev_a, height_2, i);
    }

    /* Maximum module */
    int max_num = 0;
    for (i = 0; i < n; i++)
    {
        int j = n - i - 1;
        if (max_num < height_1[i] + height_2[j] - 1)
        {
            max_num = height_1[i] + height_2[j] - 1;
        }
    }

    /* output module  */
    printf("%d", n - max_num);
    return 0;
}

  ● operation results:

  ● C + + version:

#include <iostream>
using namespace std;

/*
* Function function: find out the length of the longest adder sequence including the sequence of the ith student and the previous student.
* Parameter Description:
* [1] arr[]: Height array
* [2] height[]: It's height_1 [] and height_ The "double" of 2 [] stores an array of subsequences
* [3] N: That is to traverse the subscript i of the ith student.
*/
int find(int arr[], int height[], int N)
{
    int best_num = -1;
    int cur_height = arr[N];
    for (int i = 0; i < N; i++)
    {
        if (arr[i] < cur_height)        // First of all, the height of one of the students in front is smaller than that of the i-th student
        {
            if (height[i] > best_num)   // Secondly, if the maximum subsequence value can be updated, it will be updated.
            {
                best_num = height[i];
            }
        }
    }
    if (best_num == -1) // If the value remains unchanged, it indicates that the i-th student is currently one of the shortest
        return 1;
    else
        return best_num + 1;    // Otherwise, a value of + 1 is returned
}

int main()
{
	/* Input module */
    int a[110], rev_a[110];
    int i, n;
    cin >> n;
    for (i = 0; i < n; i++)
        cin >> a[i], res_a[n - i - 1] = a[i];
        
	/* Longest subsequence initialization module*/
    int height_1[110], height_2[110];
    for (int i = 0; i < n; i++)
        height_1[i] = height_2[i] = 1;
    for (i = 0; i < n; i++)
    {
        height_1[i] = find(a, height_1, i);
        height_2[i] = find(rev_a, height_2, i);
    }
    
    /* Maximum module */ 
	int max_num = 0;
    for (i = 0; i < n; i++)
    {
        int j = n - i - 1;
        if (max_num < height_1[i] + height_2[j] - 1)
        {
            max_num = height_1[i] + height_2[j] - 1;
        }
    }
    
    /* output module  */
    cout << n - max_num;
    return 0;
}

6, Refer to Appendix

[1] Original address: https://www.luogu.com.cn/problem/P1091.

Link to previous question: C/C + + 100 questions punch in [4 / 100] - maximum number of fusion ⭐ ️ ⭐ Test mathematics.

General contents of 100 punch outs: 🚧 🚧 …

C/C + + 100 questions punch in [5 / 100] - Chorus formation [Topic from Luogu] ⭐ ️ ⭐ ️ ⭐ ️ ⭐ ️
Tags: array, dynamic programming, monotone queue, NOIp improvement group 2004

Monday shift       
   2021/12/19