Scenario requirements
In image processing in various fields, there is often a demand for fitting surfaces. The most common is to fit inclined planes, and there are also scenes of fitting surfaces, spheres and cylinders. This paper introduces fitting cylinders.
Cylindrical fitting formula:
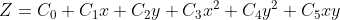
Based on this formula, we can get the coefficients of the surface to be fitted, in which C3 is powerx and C4 is powery. These two parameters are common evaluation parameters in cylindrical analysis.
In the process of fitting surfaces, there is a very important note, that is, the values of x and y. In a field, x and y need to be normalized first. Establish the grid data of x and y, which is similar to the meshgrid of matlab. For example, in the 1000 * 1000 image, the data in the first row of x is - 1, and the data in the last row is 1. The data in the first column of Y is - 1, and the data in the last column is 1. The data in the middle is also increased at equal intervals. The coefficient value thus obtained is consistent with the optical industry standard, such as the fitting method of ZYGO company.
Not much to say, the following is the specific implementation function and test code.
Function code
// Fitting cylinder
cv::Mat FitCylinder(const cv::Mat&phase)
{
cv::Mat cyc = ImageCropping(phase);
cv::Mat mask = cv::Mat::zeros(cyc.size(), CV_8UC1);
mask.setTo(255, cyc == cyc);
cv::Mat x, y, ang, mag;
UnitCart(cyc.cols, cyc.rows, x, y);
UnitPolar(x, y, mag, ang);
int samplingInterval = 1;
vector<cv::Point> points;
cv::findNonZero(mask, points);
int pointnumber = static_cast<int>(points.size());
samplingInterval = Max(samplingInterval, static_cast<int>(sqrt(pointnumber) / 100));
// Sampling, improving calculation speed,
cv::Mat sampling_roi = GridSampling(mask.size(), samplingInterval, samplingInterval);
sampling_roi.setTo(0, ~mask);
// Obtain the coordinates of the sampling point
std::vector<cv::Point> samplingidx_roi;
cv::findNonZero(sampling_roi, samplingidx_roi);
int len_sam = (int)samplingidx_roi.size();
cv::Mat ang_sampling(len_sam, 1, CV_32FC1, 0.0f);
cv::Mat mag_sampling(len_sam, 1, CV_32FC1, 0.0f);
auto tmpSam = samplingidx_roi.begin();
for (int i = 0; i < len_sam; ++i, ++tmpSam) {
int x = tmpSam->x;
int y = tmpSam->y;
ang_sampling.ptr<float>(i)[0] = ang.ptr<float>(y)[x];
mag_sampling.ptr<float>(i)[0] = mag.ptr<float>(y)[x];
}
cv::Mat phase_roi = get<float>(cyc, samplingidx_roi);
cv::Mat dst(len_sam, 6, CV_32FC1, 0.0f);
cv::Mat pow1 = mag_sampling;
cv::Mat X = pow1.mul(cosf(ang_sampling));
cv::Mat Y = pow1.mul(sinf(ang_sampling));
cv::Mat X2 = pow(X, 2.0);
cv::Mat Y2 = pow(Y, 2.0);
cv::Mat XY = X.mul(Y);
for (int i = 0; i < 6; ++i) {
switch (i) {
case 0: dst.col(i).setTo(1.0f); break; // 0
case 1: X.copyTo(dst.col(i)); break; // 1
case 2: Y.copyTo(dst.col(i)); break; // 2
case 3: X2.copyTo(dst.col(i)); break; // 3
case 4: Y2.copyTo(dst.col(i)); break; // 4
case 5: XY.copyTo(dst.col(i)); break; // 5
default: break;
}
}
cv::Mat result;
cv::solve(dst, phase_roi, result, cv::DECOMP_NORMAL); //Solve equation A'a * dst = dst in A'B,
cv::Mat temp = result.clone();
return result;
}
// Reading excel image data
cv::Mat ReadPicFromExcel(string name)
{
cv::Mat result, pic;
ifstream infile(name);
string str;
int col = 0;
while (getline(infile, str))
{
string temp;
stringstream input(str);
col = 0;
while (input >> temp)
{
if (temp == "nan")
{
pic.push_back((nan("")));
}
else {
pic.push_back((atof(temp.c_str())));
}
col++;
}
}
int number = result.rows;
int row = number / col;
result = pic.reshape(row, col);
infile.close();
return result;
}
// Image clipping
cv::Mat ImageCropping(const cv::Mat &phase) {
// Generally, the non measurement area is subject to NaN processing, so the mask drawing only needs to judge whether it is a NaN value
cv::Mat mask = cv::Mat::zeros(phase.size(), CV_8UC1);
mask.setTo(255, phase == phase);
int roi_up = 10000;
int roi_down = 0;
int roi_left = 10000;
int roi_right = 0;
int row = phase.rows;
int col = phase.cols;
for (int i = 0; i < row; i++)
{
uchar *m = mask.ptr<uchar>(i);
for (int j = 0; j < col; j++)
{
if (m[j] != 0)
{
if (j < roi_left)roi_left = j;
if (j > roi_right)roi_right = j;
if (i < roi_up)roi_up = i;
if (i > roi_down)roi_down = i;
}
}
}
int w = roi_right - roi_left;
int h = roi_down - roi_up;
// Generally, odd size is extracted to facilitate calculation
if (w % 2 == 0)w++;
if (h % 2 == 0)h++;
cv::Mat crop_phase = phase(cv::Rect(roi_left, roi_up, w, h)).clone();
return crop_phase;
}
// meshgrid
void UnitCart(int squaresizex, int squaresizey, cv::Mat& x, cv::Mat& y) {
CV_Assert(squaresizex % 2 == 1);
CV_Assert(squaresizey % 2 == 1);
x.create(squaresizey, squaresizex, CV_32FC1);
y.create(squaresizey, squaresizex, CV_32FC1);
//Set boundary
x.col(0).setTo(-1.0);
x.col(squaresizex - 1).setTo(1.0f);
y.row(0).setTo(1.0);
y.row(squaresizey - 1).setTo(-1.0f);
float deltax = 2.0f / (squaresizex - 1.0f); //Interval between two elements
float deltay = 2.0f / (squaresizey - 1.0f); //Interval between two elements
//Calculate values for other locations
for (int i = 1; i < squaresizex - 1; ++i) {
x.col(i) = -1.0f + i * deltax;
}
for (int i = 1; i < squaresizey - 1; ++i) {
y.row(i) = 1.0f - i * deltay;
}
}
// Polar coordinate transformation
void UnitPolar(cv::Mat& x, cv::Mat& y, cv::Mat& mag, cv::Mat& ang) {
//cv::cartToPolar(x, y, mag, ang, indegree); // Convert rectangular coordinates to polar coordinates
mag = cv::Mat(x.size(), x.type());
ang = cv::Mat(x.size(), x.type());
int row = mag.rows;
int col = mag.cols;
for (int i = 0; i < row; ++i)
{
float*m = mag.ptr<float>(i);
float*a = ang.ptr<float>(i);
float*xx = x.ptr<float>(i);
float*yy = y.ptr<float>(i);
for (int j = 0; j < col; ++j)
{
m[j] = sqrt(xx[j] * xx[j] + yy[j] * yy[j]);
a[j] = atan2(yy[j], xx[j]);
}
}
}
// Sampling speed up
cv::Mat GridSampling(const cv::Size& size, int rowinterval, int colinterval) {
cv::Mat dst(size, CV_8UC1, cv::Scalar(0));
//Set sampling location point
int Row = dst.rows;
int Col = dst.cols;
for (int row = 0; row < Row; row += rowinterval) {
for (int col = 0; col < Col; col += colinterval) {
dst.at<uchar>(row, col) = 255;
}
}
return dst;
}
// Get calculation data
template <typename T>
cv::Mat get(const cv::Mat& src,const std::vector<cv::Point>& idx)
{
int num = (int)idx.size();
cv::Mat dst(num, 1, src.type());
/* pragma omp parallel for Is an instruction in OpenMP,
Indicates that the next for loop will be executed by multiple threads. In addition, there can be no relationship between each loop */
#pragma omp parallel for
for (int i = 0; i < num; ++i) {
dst.at<T>(i, 0) = src.at<T>(idx[i]);
}
return dst;
}
// Image data cos processing
cv::Mat cosf(const cv::Mat& src) {
CV_Assert(src.type() == CV_32FC1);
cv::Mat dst(src.size(), src.type());
int cols = src.cols;
int rows = src.rows;
//Returns the bool value to judge whether the storage is continuous.
if (src.isContinuous() && dst.isContinuous())
{
cols *= rows;
rows = 1;
}
//Calculate cos() for each element
for (int i = 0; i < rows; i++)
{
const float* srci = src.ptr<float>(i);
float* dsti = dst.ptr<float>(i);
for (int j = 0; j < cols; j++) {
dsti[j] = std::cosf(srci[j]);
}
}
return dst;
}
// Image data sin processing
cv::Mat sinf(const cv::Mat& src) {
CV_Assert(src.type() == CV_32FC1);
cv::Mat dst(src.size(), src.type());
int cols = src.cols;
int rows = src.rows;
//Returns the bool value to judge whether the storage is continuous.
if (src.isContinuous() && dst.isContinuous())
{
cols *= rows;
rows = 1;
}
//Calculate the sin() of each element
for (int i = 0; i < rows; i++)
{
const float* srci = src.ptr<float>(i);
float* dsti = dst.ptr<float>(i);
for (int j = 0; j < cols; j++) {
dsti[j] = std::sinf(srci[j]);
}
}
return dst;
}
// Image data square processing
cv::Mat pow(cv::InputArray src, double power) {
cv::Mat dst;
cv::pow(src, power, dst);
return dst;
}
C + + test code
#include<iostream>
#include<opencv2/opencv.hpp>
#include<ctime>
#include<string>
#include<sstream>
#include<fstream>
using namespace std;
using namespace cv;
#define Max(a, b) a > b ? a : b
cv::Mat FitCylinder(const cv::Mat&phase);
cv::Mat ReadPicFromExcel(string name);
cv::Mat ImageCropping(const cv::Mat &phase);
void UnitCart(int squaresizex, int squaresizey, cv::Mat& x, cv::Mat& y);
void UnitPolar(cv::Mat& x, cv::Mat& y, cv::Mat& mag, cv::Mat& ang);
cv::Mat GridSampling(const cv::Size& size, int rowinterval, int colinterval);
template <typename T>
cv::Mat get(const cv::Mat& src, const std::vector<cv::Point>& idx);
cv::Mat cosf(const cv::Mat& src);
cv::Mat sinf(const cv::Mat& src);
cv::Mat pow(cv::InputArray src, double power);
int main(void)
{
cv::Mat phase = ReadPicFromExcel("test.xls");
cv::Mat coef = FitCylinder(phase);
for (int i = 0; i < coef.rows; ++i)
{
cout << "coef " << i << " : " << coef.at<float>(i, 0) << endl;
}
system("pause");
return 0;
}
// Fitting cylinder
cv::Mat FitCylinder(const cv::Mat&phase)
{
cv::Mat cyc = ImageCropping(phase);
cv::Mat mask = cv::Mat::zeros(cyc.size(), CV_8UC1);
mask.setTo(255, cyc == cyc);
cv::Mat x, y, ang, mag;
UnitCart(cyc.cols, cyc.rows, x, y);
UnitPolar(x, y, mag, ang);
int samplingInterval = 1;
vector<cv::Point> points;
cv::findNonZero(mask, points);
int pointnumber = static_cast<int>(points.size());
samplingInterval = Max(samplingInterval, static_cast<int>(sqrt(pointnumber) / 100));
// Sampling, improving calculation speed,
cv::Mat sampling_roi = GridSampling(mask.size(), samplingInterval, samplingInterval);
sampling_roi.setTo(0, ~mask);
// Obtain the coordinates of the sampling point
std::vector<cv::Point> samplingidx_roi;
cv::findNonZero(sampling_roi, samplingidx_roi);
int len_sam = (int)samplingidx_roi.size();
cv::Mat ang_sampling(len_sam, 1, CV_32FC1, 0.0f);
cv::Mat mag_sampling(len_sam, 1, CV_32FC1, 0.0f);
auto tmpSam = samplingidx_roi.begin();
for (int i = 0; i < len_sam; ++i, ++tmpSam) {
int x = tmpSam->x;
int y = tmpSam->y;
ang_sampling.ptr<float>(i)[0] = ang.ptr<float>(y)[x];
mag_sampling.ptr<float>(i)[0] = mag.ptr<float>(y)[x];
}
cv::Mat phase_roi = get<float>(cyc, samplingidx_roi);
cv::Mat dst(len_sam, 6, CV_32FC1, 0.0f);
cv::Mat pow1 = mag_sampling;
cv::Mat X = pow1.mul(cosf(ang_sampling));
cv::Mat Y = pow1.mul(sinf(ang_sampling));
cv::Mat X2 = pow(X, 2.0);
cv::Mat Y2 = pow(Y, 2.0);
cv::Mat XY = X.mul(Y);
for (int i = 0; i < 6; ++i) {
switch (i) {
case 0: dst.col(i).setTo(1.0f); break; // 0
case 1: X.copyTo(dst.col(i)); break; // 1
case 2: Y.copyTo(dst.col(i)); break; // 2
case 3: X2.copyTo(dst.col(i)); break; // 3
case 4: Y2.copyTo(dst.col(i)); break; // 4
case 5: XY.copyTo(dst.col(i)); break; // 5
default: break;
}
}
cv::Mat result;
cv::solve(dst, phase_roi, result, cv::DECOMP_NORMAL); //Solve equation A'a * dst = dst in A'B,
cv::Mat temp = result.clone();
return result;
}
// Reading excel image data
cv::Mat ReadPicFromExcel(string name)
{
cv::Mat result, pic;
ifstream infile(name);
string str;
int col = 0;
while (getline(infile, str))
{
string temp;
stringstream input(str);
col = 0;
while (input >> temp)
{
if (temp == "nan")
{
pic.push_back((nan("")));
}
else {
pic.push_back((atof(temp.c_str())));
}
col++;
}
}
int number = result.rows;
int row = number / col;
result = pic.reshape(row, col);
infile.close();
return result;
}
// Image clipping
cv::Mat ImageCropping(const cv::Mat &phase) {
// Generally, the non measurement area is subject to NaN processing, so the mask drawing only needs to judge whether it is a NaN value
cv::Mat mask = cv::Mat::zeros(phase.size(), CV_8UC1);
mask.setTo(255, phase == phase);
int roi_up = 10000;
int roi_down = 0;
int roi_left = 10000;
int roi_right = 0;
int row = phase.rows;
int col = phase.cols;
for (int i = 0; i < row; i++)
{
uchar *m = mask.ptr<uchar>(i);
for (int j = 0; j < col; j++)
{
if (m[j] != 0)
{
if (j < roi_left)roi_left = j;
if (j > roi_right)roi_right = j;
if (i < roi_up)roi_up = i;
if (i > roi_down)roi_down = i;
}
}
}
int w = roi_right - roi_left;
int h = roi_down - roi_up;
// Generally, odd size is extracted to facilitate calculation
if (w % 2 == 0)w++;
if (h % 2 == 0)h++;
cv::Mat crop_phase = phase(cv::Rect(roi_left, roi_up, w, h)).clone();
return crop_phase;
}
// meshgrid
void UnitCart(int squaresizex, int squaresizey, cv::Mat& x, cv::Mat& y) {
CV_Assert(squaresizex % 2 == 1);
CV_Assert(squaresizey % 2 == 1);
x.create(squaresizey, squaresizex, CV_32FC1);
y.create(squaresizey, squaresizex, CV_32FC1);
//Set boundary
x.col(0).setTo(-1.0);
x.col(squaresizex - 1).setTo(1.0f);
y.row(0).setTo(1.0);
y.row(squaresizey - 1).setTo(-1.0f);
float deltax = 2.0f / (squaresizex - 1.0f); //Interval between two elements
float deltay = 2.0f / (squaresizey - 1.0f); //Interval between two elements
//Calculate values for other locations
for (int i = 1; i < squaresizex - 1; ++i) {
x.col(i) = -1.0f + i * deltax;
}
for (int i = 1; i < squaresizey - 1; ++i) {
y.row(i) = 1.0f - i * deltay;
}
}
// Polar coordinate transformation
void UnitPolar(cv::Mat& x, cv::Mat& y, cv::Mat& mag, cv::Mat& ang) {
//cv::cartToPolar(x, y, mag, ang, indegree); // Convert rectangular coordinates to polar coordinates
mag = cv::Mat(x.size(), x.type());
ang = cv::Mat(x.size(), x.type());
int row = mag.rows;
int col = mag.cols;
for (int i = 0; i < row; ++i)
{
float*m = mag.ptr<float>(i);
float*a = ang.ptr<float>(i);
float*xx = x.ptr<float>(i);
float*yy = y.ptr<float>(i);
for (int j = 0; j < col; ++j)
{
m[j] = sqrt(xx[j] * xx[j] + yy[j] * yy[j]);
a[j] = atan2(yy[j], xx[j]);
}
}
}
// Sampling speed up
cv::Mat GridSampling(const cv::Size& size, int rowinterval, int colinterval) {
cv::Mat dst(size, CV_8UC1, cv::Scalar(0));
//Set sampling location point
int Row = dst.rows;
int Col = dst.cols;
for (int row = 0; row < Row; row += rowinterval) {
for (int col = 0; col < Col; col += colinterval) {
dst.at<uchar>(row, col) = 255;
}
}
return dst;
}
// Get calculation data
template <typename T>
cv::Mat get(const cv::Mat& src,const std::vector<cv::Point>& idx)
{
int num = (int)idx.size();
cv::Mat dst(num, 1, src.type());
/* pragma omp parallel for Is an instruction in OpenMP,
Indicates that the next for loop will be executed by multiple threads. In addition, there can be no relationship between each loop */
#pragma omp parallel for
for (int i = 0; i < num; ++i) {
dst.at<T>(i, 0) = src.at<T>(idx[i]);
}
return dst;
}
// Image data cos processing
cv::Mat cosf(const cv::Mat& src) {
CV_Assert(src.type() == CV_32FC1);
cv::Mat dst(src.size(), src.type());
int cols = src.cols;
int rows = src.rows;
//Returns the bool value to judge whether the storage is continuous.
if (src.isContinuous() && dst.isContinuous())
{
cols *= rows;
rows = 1;
}
//Calculate cos() for each element
for (int i = 0; i < rows; i++)
{
const float* srci = src.ptr<float>(i);
float* dsti = dst.ptr<float>(i);
for (int j = 0; j < cols; j++) {
dsti[j] = std::cosf(srci[j]);
}
}
return dst;
}
// Image data sin processing
cv::Mat sinf(const cv::Mat& src) {
CV_Assert(src.type() == CV_32FC1);
cv::Mat dst(src.size(), src.type());
int cols = src.cols;
int rows = src.rows;
//Returns the bool value to judge whether the storage is continuous.
if (src.isContinuous() && dst.isContinuous())
{
cols *= rows;
rows = 1;
}
//Calculate the sin() of each element
for (int i = 0; i < rows; i++)
{
const float* srci = src.ptr<float>(i);
float* dsti = dst.ptr<float>(i);
for (int j = 0; j < cols; j++) {
dsti[j] = std::sinf(srci[j]);
}
}
return dst;
}
// Image data square processing
cv::Mat pow(cv::InputArray src, double power) {
cv::Mat dst;
cv::pow(src, power, dst);
return dst;
}
Test effect
Figure 1 # cylindrical gray image
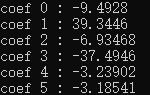Fig. 2} fitting results
Fig. 3 3D visual diagram
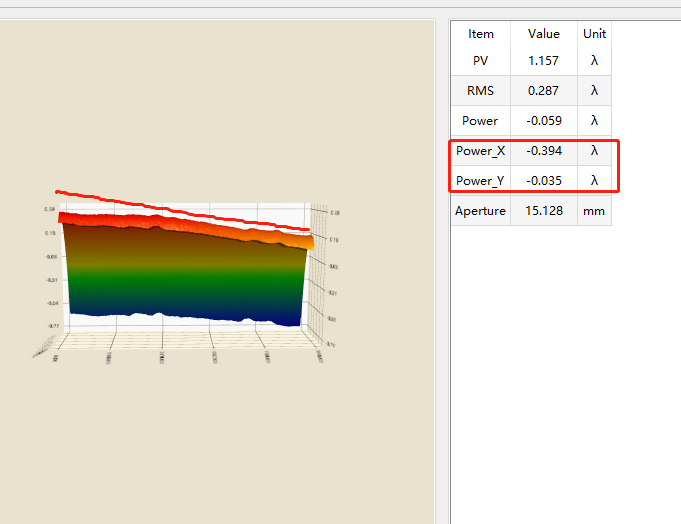Fig. 4 data comparison
In the test case, I loaded a cylindrical data. Because the values of the interferometry results are generally very low, I multiplied the values by 100, so that the gray image can clearly see the difference between black and white, as shown in Figure 1, and the inclination can also be seen in Figure 4. The white area is the part with a value greater than 0; Because the area I intercepted in VS is not completely consistent with the area intercepted in our software, the values of powerx and powery are different. As long as the magnitude is consistent, there is no error; As shown in Figure 2, the output of VS is divided by 100 and then compared. coef3 is powerx and coef4 is powery.
If the function can be improved, you are very welcome to point out that why not make progress together~
If the article helps you, you can point a praise to let me know, I will be very happy ~ come on!