Zero. Preface

This chapter mainly explains the container stack, queue and priority in C + +_ Queue (priority queue, equivalent to heap in data structure), which is simulated after being familiar with the use

1, Introduction and use of stack

1. Introduction to stack

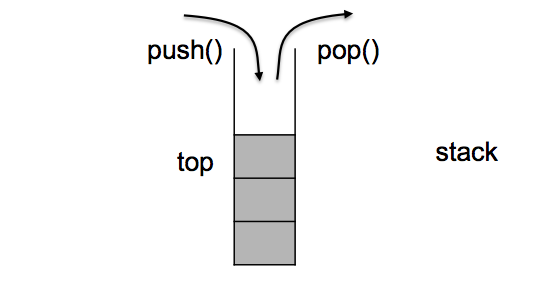
1. stack is a container adapter, which is specially used in the context of last in first out operation. Its deletion can only insert and extract elements from one end of the container

2. Stack is implemented as a container adapter. A container adapter encapsulates a specific class as its underlying container and provides a set of specific member functions to access its elements. With a specific class as its underlying element, the tail of a specific container (i.e. the top of the stack) is pushed in and popped out

3. The underlying container of stack can be any standard container class template or some other specific container classes. These container classes should support the following operations:
   Empty: empty judgment
   back: get tail element operation
   push_back: tail insert element operation
   pop_back: delete element from the tail

4. The standard containers vector, deque and list all meet these requirements. By default, if no specific underlying container is specified for the stack, deque (double ended queue, also a container) is used by default

• Diagram:
  

2. Use of stack

Function description	Interface description
stack()	Construct an empty stack
empty()	Check whether the stack is empty
size()	Returns the number of elements in the stack
top()	Returns a reference to the top element of the stack
push()	Press the element val into the stack
pop()	Pop up the elements at the end of the stack

• Example 1: implementing queue with stack

Buckle link: 232. Implement LeetCode with stack (LeetCode CN. Com)

• Implementation idea:

Two stacks are needed here. One is used to input data and the other is used to output data

push: only data is pushed into the data stack

pop: only let the data stack out of the data stack. If there is no data, all the data in the data must be out of the stack in turn and then into the data stack out of the data stack

This enables the queue first in first out feature

• Implementation code:

class MyQueue {
public:
    MyQueue() {
//There is no need to write anything. For a custom type, stack will automatically call its constructor
    }
    
    void push(int x) {
        //Stack data
        st1.push(x);
    }
    
    int pop() {
        int ret;
        //Whether there is data out of the stack
        if(!st2.empty())
        {
            ret=st2.top();
            st2.pop();
            return ret;
        }
        else
        {
            //Putting data on and off the stack
            while(!st1.empty())
            {
                st2.push(st1.top());
                st1.pop();
            }
            //pop data
            ret=st2.top();
            st2.pop();
            return ret;
        }
    }
    
    int peek() {
        if(!st2.empty())
        {
            return st2.top();
        }
        else
        {
            while(!st1.empty())
            {
                st2.push(st1.top());
                st1.pop();
            }
            return st2.top();
        }
    }
    
    bool empty() {
        return st1.empty()&&st2.empty();
    }
    private:
    stack<int> st1;
    stack<int> st2;
};

2, Introduction and use of queue

1. Introduction to queue

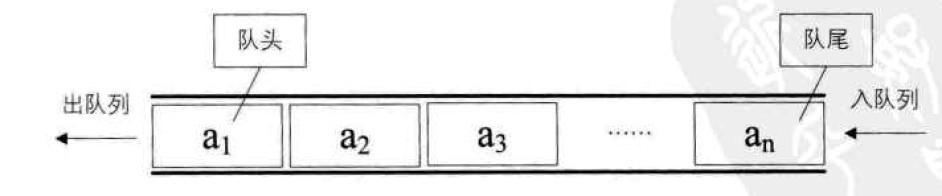
1. A queue is a container adapter designed to operate in a FIFO context (first in first out), where elements are inserted from one end of the container and extracted from the other

2. Queue is implemented as a container adapter, which encapsulates a specific container class as its underlying container class, and queue provides a set of specific member functions to access its elements; Elements enter the queue from the end of the queue and exit the queue from the head of the queue

3. The underlying container can be one of the standard container class templates or other specially designed container classes. The bottom container shall support at least the following operations:
   Empty: check whether the queue is empty
   size: returns the number of valid elements in the queue
   front: returns a reference to the queue header element
   back: returns a reference to the end of the queue element
   push_back: enter the queue at the end of the queue
   pop_front: exit the queue at the head of the queue

4. The standard container classes deque and list meet these requirements. By default, if no container class is specified for queue instantiation, the standard container deque (double ended queue) is used

• Diagram:

2. Use of queue

Function declaration	Interface description
queue()	Construct an empty queue
empty()	Check whether the queue is empty. If yes, return true; otherwise, return false
size()	Returns the number of valid elements in the queue
front()	Returns a reference to the queue header element
back()	Returns a reference to the end of queue element
push()	Queue the element val at the end of the queue
pop()	Remove the queue header element from the queue

• Example 2: implementing stack with queue

Buckle link: 225. Implement LeetCode with queue (LeetCode CN. Com)

• Implementation idea:

We also need two queues here

push: queue to the queue with data

pop: send the data with data queue (except the last data) out of the queue in turn, merge it into another queue, and finally give the last data to the queue

In order to realize the first in and last out characteristics of the stack

• Implementation code:

class MyStack {
public:
    MyStack() {

    }
    
    void push(int x) {
        //Incoming data queue
        if(q1.empty())
        {
            q2.push(x);
        }
        else
        {
            q1.push(x);
        }
    }
    
    int pop() {
        //Determine which queue has data
        queue<int>*q=&q1;
        queue<int>*nonq=&q2;
        if(q1.empty())
        {
            q=&q2;
            nonq=&q1;
        }
        //Exit queue and re-enter queue
        while(q->size()>1)
        {
            nonq->push(q->front());
            q->pop();
        }
        //pop data
        int ret=q->front();
        q->pop();
        return ret;
    }
    
    int top() {
        if(!q1.empty())
        {
            return q1.back();
        }
        else
        {
            return q2.back();
        }
    }
    
    bool empty() {
        return q1.empty()&&q2.empty();
    }
    private:
    queue<int> q1;
    queue<int> q2;
};

3, Priority_ Introduction and use of queue

1,priority_ Introduction to queue

1. Priority queue is a container adapter. According to strict weak sorting criteria, its first element is always the largest of its contained elements (the default priority queue)

2. A priority queue is similar to a heap, where elements can be inserted at any time, and only the largest heap element (the top element in the priority queue) can be retrieved

3. The priority queue is implemented as a container adapter, which encapsulates a specific container class as its underlying container class, and queue provides a set of specific member functions to access its elements. The element pops from the "tail" of a particular container, which is called the top of the priority queue

4. The underlying container can be any standard container class template or other specially designed container classes. The container should be accessible through a random access iterator and support the following operations:

empty(): check whether the container is empty

size(): returns the number of valid elements in the container

front(): returns the reference of the first element in the container

​ push_back(): inserts an element at the end of the container

​ pop_back(): delete the container tail element

1. The standard container classes vector and deque meet these requirements. By default, if there is no specific priority_ If the queue class instantiates the specified container class, vector is used

2. Random access iterators need to be supported to always maintain the heap structure internally. The container adapter automatically calls the algorithm function make when needed_ heap,push_heap and pop_heap to automate this operation (also encapsulation)

Note: take a pile as an example

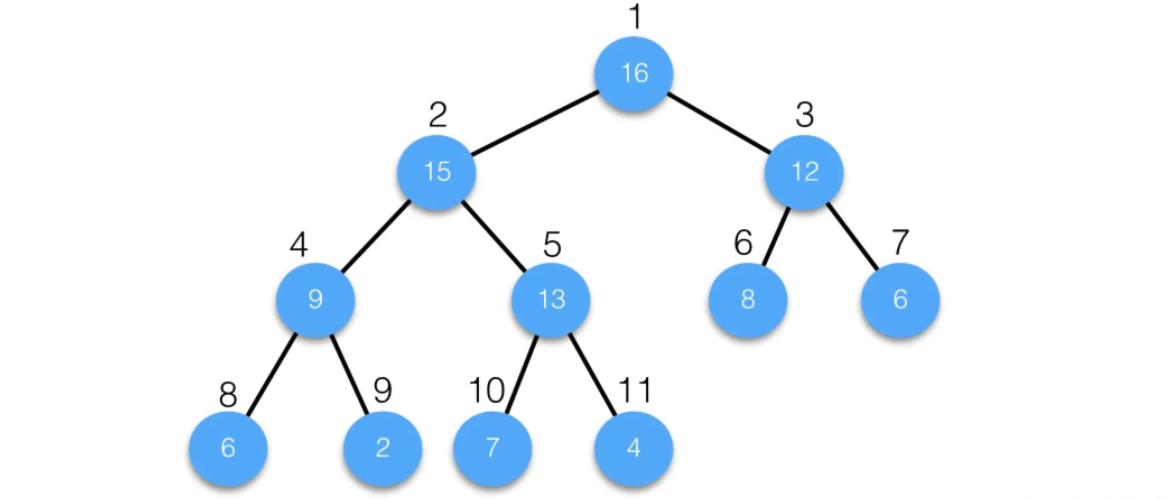
• Diagram: physical structure

• Diagram: logical structure

• Summary:

By default, the priority queue uses vector as its underlying data storage container, and the heap algorithm is used on the vector to construct the elements in the vector into a heap structure, so priority_queue is the heap. Priority can be considered for all locations where the heap needs to be used_ queue

Note: by default, priority_queue is a lot

2,priority_ Use of queue

Function declaration	Interface description
priority_queue()/priority_queue(first, last)	Construct an empty priority queue
empty( )	Check whether the priority queue is empty. If yes, return true; otherwise, return false
top( )	Returns the largest (smallest) element in the priority queue, that is, the top element of the heap
push(x)	Insert element x in priority queue
pop()	Delete the largest (smallest) element in the priority queue, that is, the top of the heap element

• Use example:

#include <vector>
#include <queue>
#Include < functional > / / header file of greater algorithm

void TestPriorityQueue()
{
	// By default, a lot is created, and its bottom layer is compared according to the less than sign
	vector<int> v{ 3,2,7,6,0,4,1,9,8,5 };
	priority_queue<int> q1;
	for (auto& e : v)
		q1.push(e);
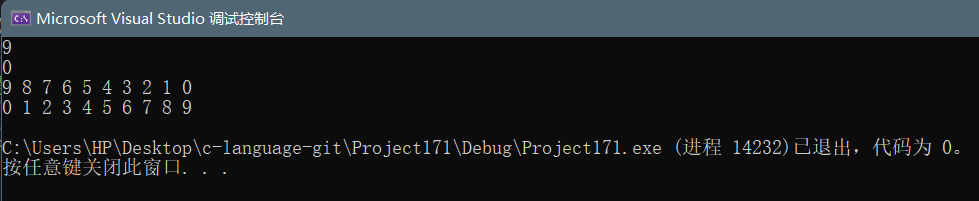
	cout << q1.top() << endl;
	// If you want to create a small heap, change the third template parameter to greater comparison mode
	priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
	cout << q2.top() << endl;
	// Heap sort output data
	while (!q1.empty())
	{
		cout << q1.top() << " ";
		q1.pop();
	}cout << endl;
	while (!q2.empty())
	{
		cout << q2.top() << " ";
		q2.pop();
	}cout << endl;
}

• result:

Note: if in priority_ The user needs to provide the overload of > or < in the user-defined type to put the data of the user-defined type in the queue

• Example:

class Date
{
public:
	Date(int year = 1900, int month = 1, int day = 1)
		: _year(year)
		, _month(month)
		, _day(day)
	{}
	bool operator<(const Date& d)const
	{
		return (_year < d._year) ||
			(_year == d._year && _month < d._month) ||
			(_year == d._year && _month == d._month && _day < d._day);
	}
	bool operator>(const Date& d)const
	{
		return (_year > d._year) ||
			(_year == d._year && _month > d._month) ||
			(_year == d._year && _month == d._month && _day > d._day);
	}
	friend ostream& operator<<(ostream& _cout, const Date& d)
	{
		_cout << d._year << "-" << d._month << "-" << d._day;
		return _cout;
	}
private:
	int _year;
	int _month;
	int _day;
};
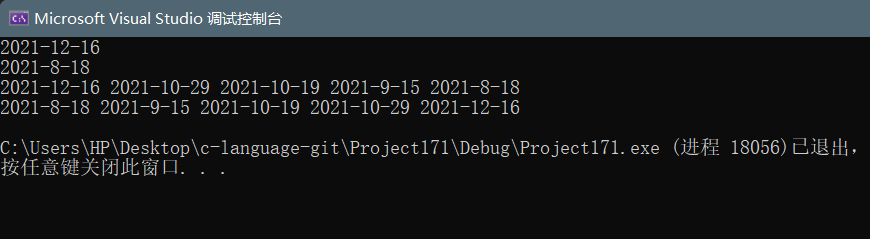
void TestPriorityQueue2()
{
	// The user needs to provide an overload of < in the user-defined type
	priority_queue<Date> q1;
	q1.push(Date(2021, 10, 19));
	q1.push(Date(2021, 10, 29));
	q1.push(Date(2021, 12, 16));
	q1.push(Date(2021, 8, 18));
	q1.push(Date(2021, 9, 15));
	cout << q1.top() << endl;
	// If you want to create a small heap, you need to provide an overload of >
	priority_queue<Date, vector<Date>, greater<Date>> q2;
	q2.push(Date(2021, 10, 19));
	q2.push(Date(2021, 10, 29));
	q2.push(Date(2021, 12, 16));
	q2.push(Date(2021, 8, 18));
	q2.push(Date(2021, 9, 15));
	cout << q2.top() << endl;
	while (!q1.empty())
	{
		cout << q1.top() << " ";
		q1.pop();
	}cout << endl;
	while (!q2.empty())
	{
		cout << q2.top() << " ";
		q2.pop();
	}cout << endl;
}

• result:

4, Container adapter

• Concept:

1. An adapter is a design pattern (a design pattern is a set of code design experience that is repeatedly used, known by most people, classified and cataloged)

2. This pattern is to convert the interface of a class into another interface that the customer wants

3. That is, the container encapsulates its interface appropriately to get the desired functions and features

• stack/queue/priority_ The underlying structure of the queue:

Although elements can also be stored in stack and queue, they are not divided into the ranks of containers in STL, but called container adapters

Because stack and queue only wrap the interfaces of other containers (in STL, stack and queue use deque by default, and priority_queue uses vector to encapsulate and implement its features)

• Diagram:

5, A brief introduction to deque

Note: deque is only for understanding

• Introduction:

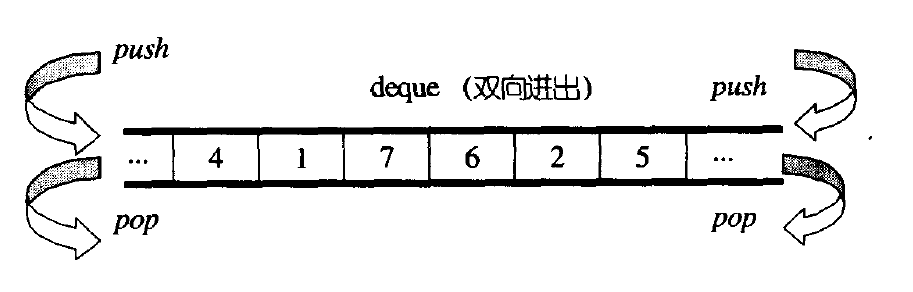
1. Deque (double ended queue) is a data structure with double openings in "continuous" space

2. Insert and delete operations can be performed at both ends of the head and tail, and the time complexity is O(1)

3. Compared with vector, deque has high head insertion efficiency and does not need to move elements; Compared with list, the space utilization rate is relatively high

• Diagram:

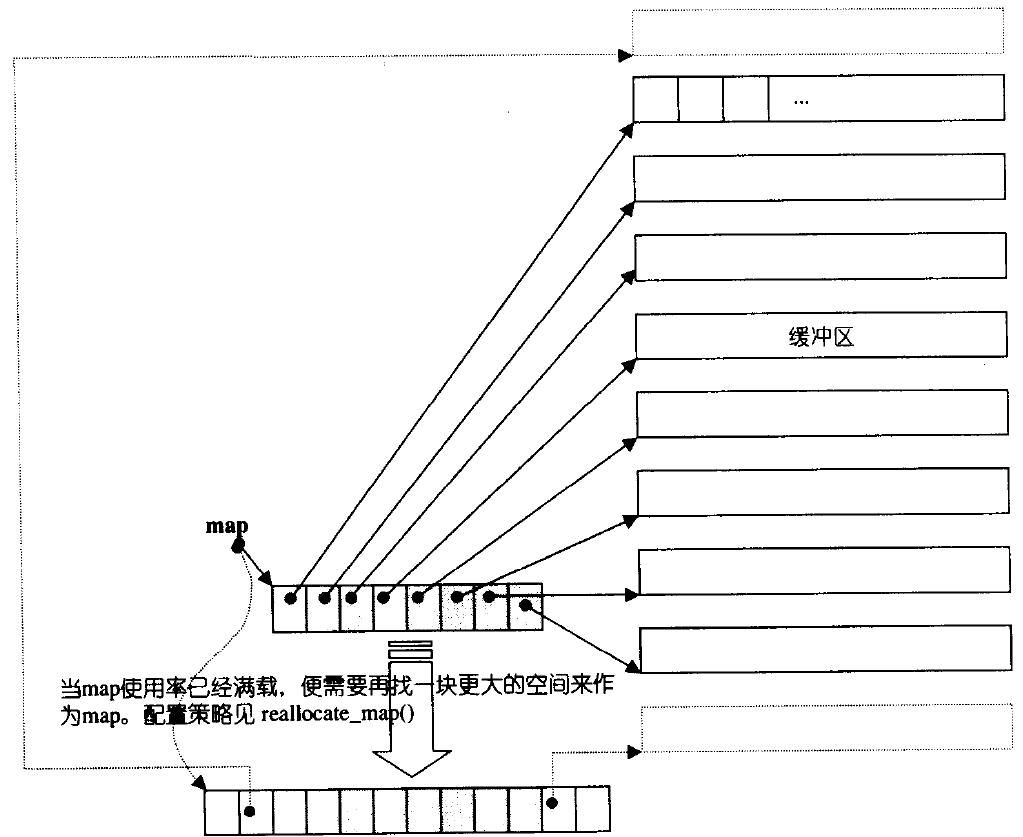
1. deque is not really a continuous space, but is composed of small continuous spaces (similar to a dynamic two-dimensional array)

• Diagram:

1. The bottom layer of the double ended queue is an imaginary continuous space, which is actually piecewise continuous. In order to maintain its "overall continuity" and the illusion of random access, it falls on the iterator of deque, so the design of the iterator of deque is more complex

• Diagram:

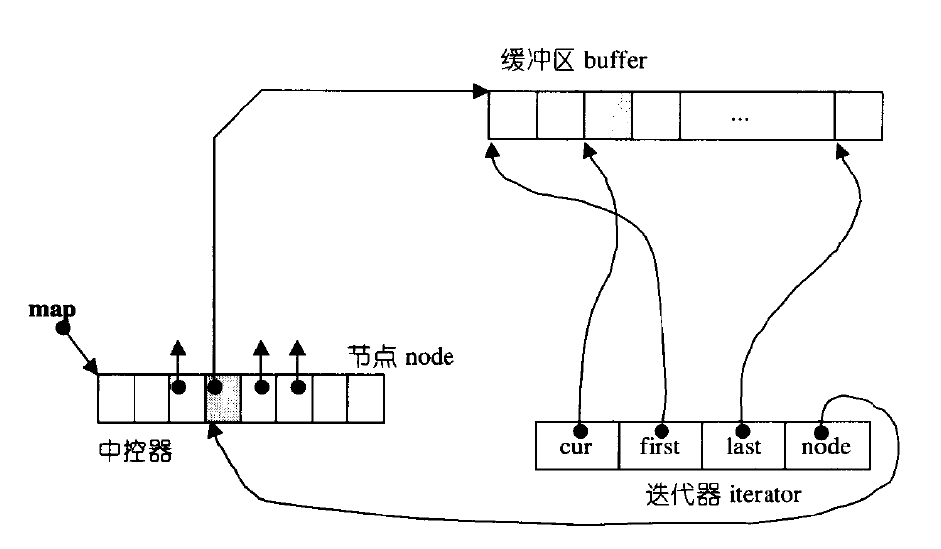
• How iterators maintain space:

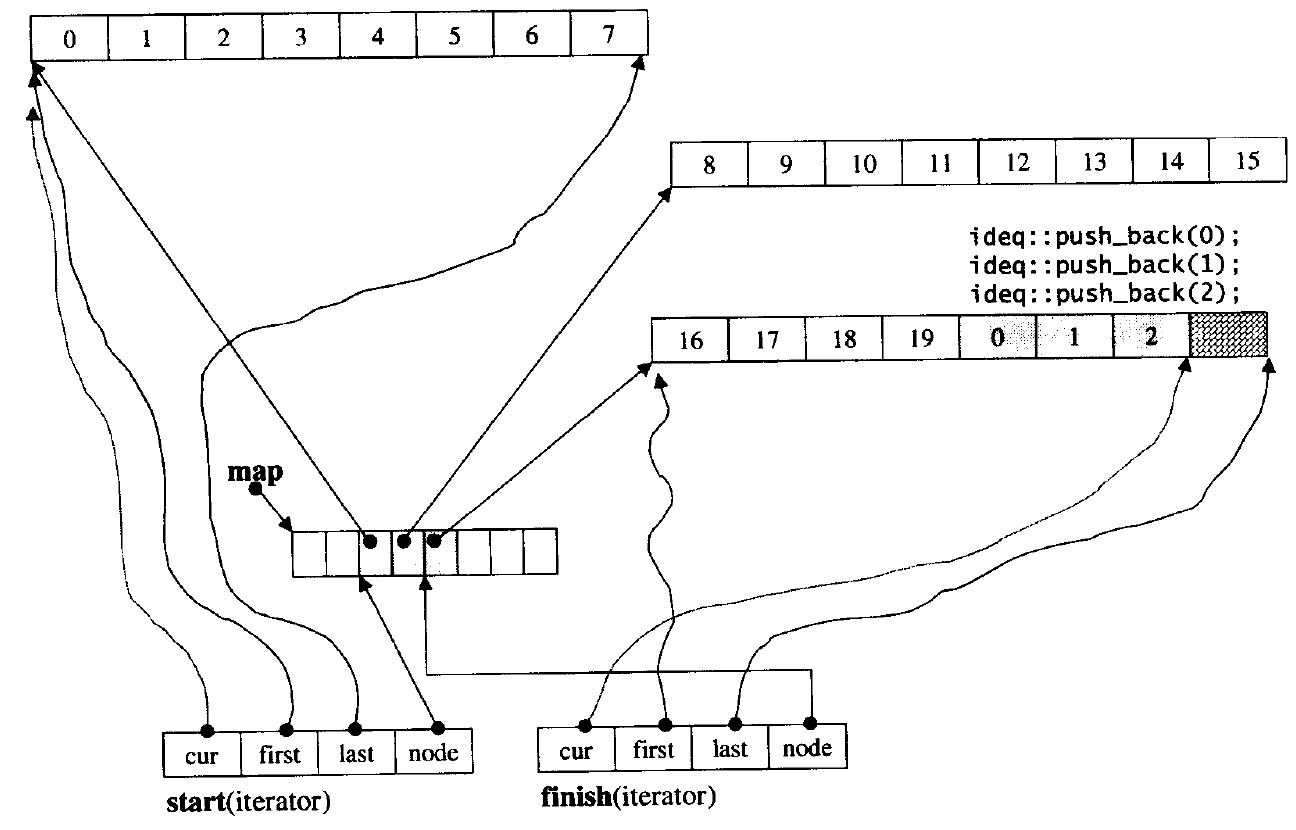
• summary

1. Advantages:

Compared with vector, deque does not need to move elements during header insertion and deletion, which is particularly efficient, and does not need to move a large number of elements during capacity expansion; Compared with list, its bottom layer is continuous space, which has high space utilization. It does not need to store additional fields and can be accessed randomly (combining the advantages of vector and list)

1. Disadvantages:

It is not suitable for traversal. The iterator of deque needs to frequently detect whether it moves to the boundary of a small space, resulting in low efficiency (therefore, in practice, when linear structure is required, vector and list are given priority in most cases. Deque is not widely used, and one application that can be seen at present is that STL uses it as the underlying data structure of stack and queue)

1. Why choose deque as the underlying default container

1. Stack and queue do not need to be traversed (therefore, stack and queue do not have iterators), but only need to operate at one or both ends (avoiding the deque defect)

2. When the elements in stack grow, deque is more efficient than vector (there is no need to move a large amount of data during capacity expansion); When the elements in the queue grow, deque not only has high efficiency, but also has high memory utilization (reflecting the advantages of deque)

6, Simulation Implementation of stack

• Implementation code:

namespace cole
{
	template<class T,class Container=std::deque<T>>
	class stack
	{
	public:
		void push(const T& x)
		{
			con.push_back(x);
		}

		void pop()
		{
			con.pop_back();
		}

		const T& top()
		{
			return con.back();
		}

		size_t size()
		{
			return con.size();
		}

		bool empty()
		{
			return con.empty();
		}
	private:
		Container con;
	};
}

7, Simulation Implementation of queue

• Implementation code:

namespace cole
{
	template<class T,class Container=std::deque<T>>
	class queue
	{
	public:
		void push(const T& x)
		{
			con.push_back(x);
		}

		void pop()
		{
			con.pop_front();
		}

		const T& front()
		{
			return con.front();
		}

		const T& back()
		{
			return con.back();
		}

		size_t size()
		{
			return con.size();
		}

		bool empty()
		{
			return con.empty();
		}
	private:
		Container con;
	};
}

8, Priority_ Simulation Implementation of queue

• Implementation code:

namespace cole
{
	//Imitation function - function object (this kind of object can be used like a function)
	template<class T>
	struct less
	{
		bool operator()(const T& a, const T& b)
		{
			return a < b;
		}
	};
	template<class T>
	struct greater
	{
		bool operator()(const T& a, const T& b)
		{
			return a > b;
		}
	};

	template<class T,class Container=std::deque<T>,class Compare=less<T>>//Default heap
	class priority_queue
	{
	public:
		//Adjust data up
		void Adjustup(size_t child)
		{
			size_t parent = (child - 1) / 2;
			while (child > 0)
			{
				//Adjust
				if (cmp(con[parent], con[child]))
				{
					swap(con[child], con[parent]);
					child = parent;
					parent = (child - 1) / 2;
				}
				else
				{
					break;
				}
			}
		}
		//Adjust data down
		void Adjustdown(size_t parent)
		{
			size_t child = parent * 2 + 1;
			while (child < con.size())
			{
				//Compare left and right child nodes
				if (child + 1 < con.size() && cmp(con[child], con[child + 1]))
				{
					++child;
				}
				//Adjust
				if (cmp(con[parent], con[child]))
				{
					swap(con[child], con[parent]);
					parent = child;
					child = parent * 2 + 1;
				}
				else
				{
					break;
				}
			}
		}

		void push(const T& x)
		{
			con.push_back(x);
			Adjustup(con.size() - 1);
		}

		void pop()
		{
			swap(con[0], con[con.size() - 1]);
			con.pop_back();
			Adjustdown(0);
		}

		const T& top()
		{
			return con[0];
		}

		size_t size()
		{
			return con.size();
		}

		bool empty()
		{
			return con.empty();
		}
	private:
		Container con;
		Compare cmp;
	};
}