summary

There is A sequence A composed of N Boolean values, which gives some restrictive relations, such as A[x] AND A[y]=0, A[x] OR A[y] OR A[z]=1. It is necessary to determine the value of A[0 * n − 1] so that it meets all restrictive relations. This is called the SAT problem (it has been determined that the SAT problem that is not 2-SAT is NP complete). In particular, if there are only two elements in each restriction relationship, it is called the 2-SAT problem.

algorithm

We can divide each point into two points. One represents true and the other represents false. We can traverse the point pair. If neither of the two points is selected, first assume false, and DFS along the edge marks all the points it can reach as selected. If both points of a point pair are selected in the dyeing process, That is, if a value is false, the value will be true, which means that the assumption is contradictory. Clear the mark along the road, and then try to select true for DFS. If it fails again, it means that there is no solution that meets all conditions. After one point of all point pairs is selected, we get an overall selection method to meet all the subject conditions.

Note: true and false here are not absolute, depending on the actual situation! For ex amp le: wife (true) & husband (false), work & vacation, try to be opposite!

Algorithm example

Next, an example is given to illustrate the execution process of the algorithm.

We have A sequence consisting of # 3 Boolean values # A, with the following restrictions:

• A[0] OR A[1]=1
• A[1] AND A[2]=1

First, we split the points and then connect the edges. According to the first restriction, we connect the "false" of A[0] and the "true" of A[1], and the "false" of A[1] and the "true" of A[0] to connect the directed edges, because as long as one of the two is not "1 \ 1", the other must be "1". According to the second condition, connect the false of A[1] and the true of A[1] to the directed edge, and connect the false of A[2] and the true of A[2] to the directed edge, because as long as one is not {1, this equation cannot be established. Then the picture will look like this.

We start with "0" and find that "true" and "false" of "0" are not selected, so try to select "false" first.

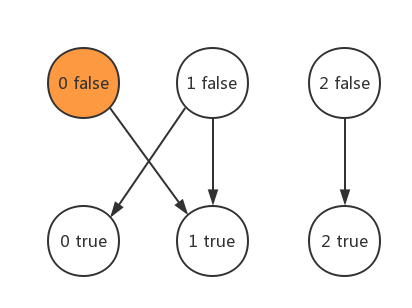
Select along the road from this point, and select "1" as "true".

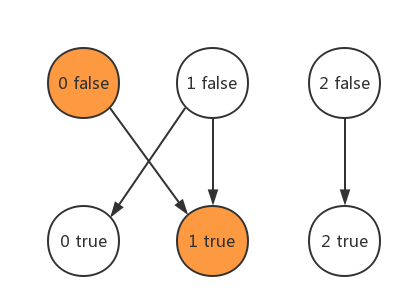
At this time, all the routes from "false" of "0" are selected. Let's look at ， 1. If ， 1 ， has been selected ， true ， we won't search this point. If you try to choose "false", your "true" will also be selected, which means that "2" cannot choose "false", then try to choose "true", find that it can, and the selection is completed.

At this point, one of all point pairs is selected. If the selection is successful, we get a set of solutions that meet all constraints.

The time complexity is O(VE) and the space complexity is S(V+E).

C + + sample code

#include <iostream>
#include <cstring>
using namespace std;
const int MAX_N = 100;  // Upper limit of point
const int MAX_M = 10000;  // Upper limit of edge
struct edge {
    int v, next;
} E[MAX_M];
int p[MAX_N * 2], eid;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    e[eid].v = v;
    e[eid].next = p[u];
    p[u] = eid++;
}
int n, m;  // n represents the number of points and m represents the number of sides
bool selected[MAX_N * 2]; // Mark whether each point pair is selected. Each point pair is 2*i and 2*i+1
int S[MAX_N * 2]; // Mark the points passed by this selection
int c; // Points selected this time
bool dfs(int u) {
    if (selected[u ^ 1]) {
        return false;//Conflict with assumptions
    }
    if (selected[u]) {
        return true;//Same as assumption
    }
    selected[u] = true;
    S[c++] = u;
    for (int i = p[u]; i != -1; i = E[i].next) {
        int v = E[i].v;
        if (!dfs(v)) {
            return false;
        }
    }
    return true;
}
bool Two_SAT(int n) {
    for(int i = 0; i < 2 * n; i += 2) {
        if (!selected[i] && !selected[i + 1]) {
            c = 0;
            if (!dfs(i)) {
                while (c > 0) {
                    selected[S[--c]] = false; // Clear the selection along the road after failure
                }
                if (!dfs(i + 1)) {
                    return false;
                }
            }
        }
    }
    return true;
}
int main() {
    init();
    memset(selected,false,sizeof(selected));
    cin>>N>>M;
    for (int i=0;i<M;i++){
        int k,x,y;
        cin>>k>>x>>y;
        if (k==0){
            insert(2*x,2*x+1);
            insert(2*y,2*y+1);
        }else{
            insert(2*x,2*y+1);
            insert(2*y,2*x+1);
        }
    }
    if (Two_SAT(N)){
        cout<<"YES"<<endl;
    }else{
        cout<<"NO"<<endl;
    }
    return 0;
}