Time complexity of sorting algorithm

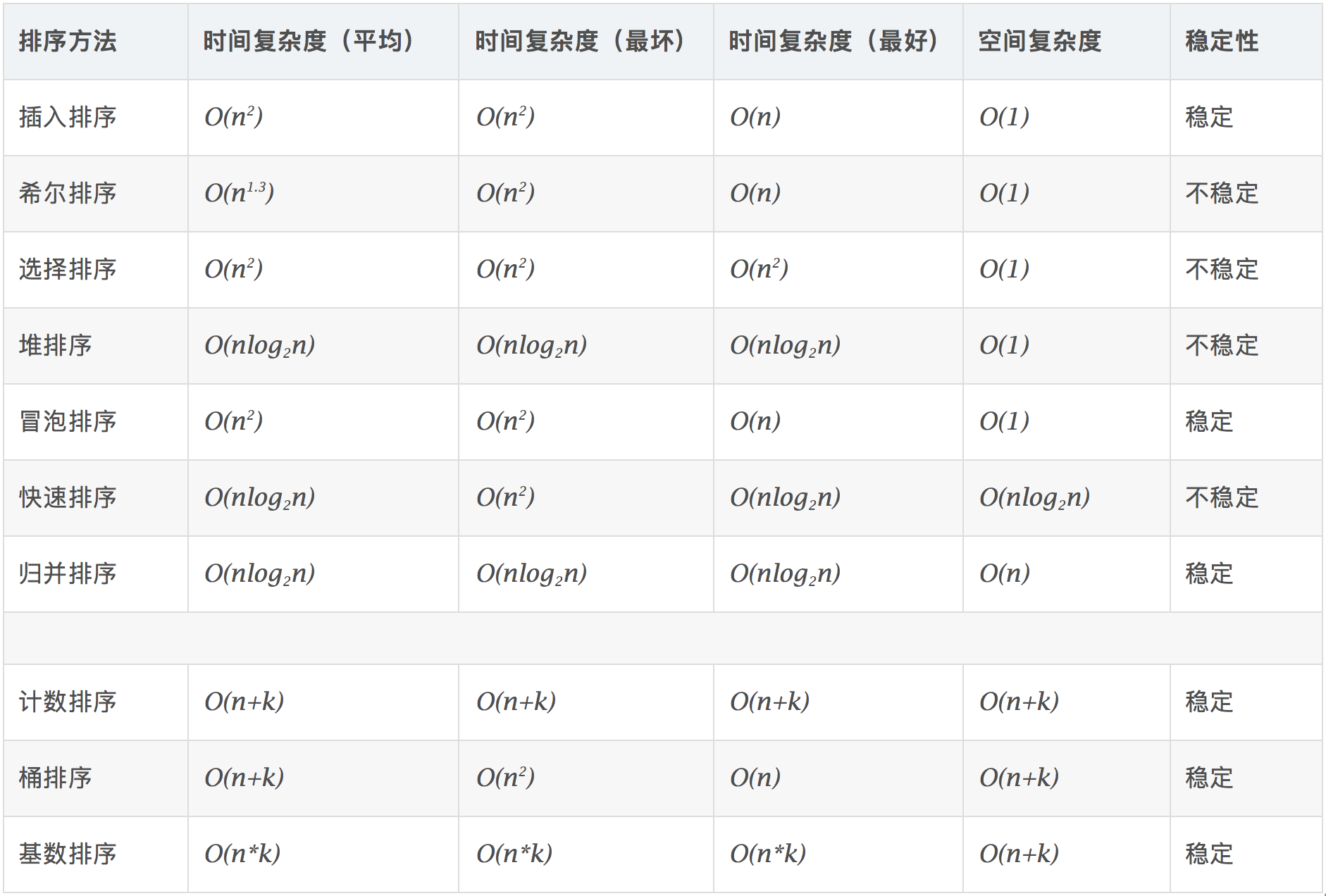
The time complexity of common algorithms is as follows: Ο (1) < Ο (log2n) < Ο (n) < Ο (nlog2n) < Ο (n2) < Ο (n3) ＜ ＜Ο(2n)＜Ο(n!)

Support the generic merge sort of STL

1. Let's create a header file, algorithm? Sort. H. here's the content

#include <vector>

template <class Iterator, class Strategy>
inline void MergeSort(Iterator _First, Iterator _Last,
	Strategy _Strategy)
{
	if (_First == _Last || _Last - _First == 1)
		return;
	typedef iterator_traits<Iterator>::difference_type difference_type;
	difference_type differenceType = (_Last - _First) / 2;
	MergeSort(_First, _First + differenceType, _Strategy);
	MergeSort(_First + differenceType, _Last, _Strategy);
	_merge(_First, _First + differenceType, _First + differenceType, _Last, _Strategy);
}

template <class Iterator, class Strategy>
inline void _merge(Iterator _Part1First, Iterator _Part1Last,
	Iterator _Part2First, Iterator _Part2Last,
	Strategy _Strategy)
{
	Iterator itPart1 = _Part1First;
	Iterator itPart2 = _Part2First;

	typedef iterator_traits<Iterator>::value_type value_type;
	vector<value_type> result;

	while (itPart1 != _Part1Last && itPart2 != _Part2Last){
		if (_Strategy(*itPart1, *itPart2)){
			result.push_back(*itPart1);
			itPart1++;
		}
		else{
			result.push_back(*itPart2);
			itPart2++;
		}
	}

	if (itPart1 < _Part1Last)
		result.insert(result.end(), itPart1, _Part1Last);
	if (itPart2 < _Part2Last)
		result.insert(result.end(), itPart2, _Part2Last);

	itPart1 = _Part1First;
	itPart2 = _Part2First;
	vector<value_type>::iterator it = result.begin();
	while (it != result.end()){
		if (itPart1 != _Part1Last){
			*itPart1 = *it;
			itPart1++;
		}
		else if (itPart2 != _Part2Last){
			*itPart2 = *it;
			itPart2++;
		}
		it++;
	}
}

2. The following is the calling procedure

#include "stdafx.h"
#include <iostream>
#include "algorithm_sort.h"
#include <stdlib.h>
using namespace std;
struct MyStruct
{
	int num;
	double age;
};

template<class T>
bool Max(T a, T b)//Sorting strategy
{
	return a.num < b.num;
}

int _tmain(int argc, _TCHAR* argv[])
{
	MyStruct myStruct;
	myStruct.num = 12;
	myStruct.age = 1.;

	vector<MyStruct> data;
	data.push_back(myStruct);
	myStruct.num = 15;
	data.push_back(myStruct);
	myStruct.num = 9;
	data.push_back(myStruct);
	myStruct.num = 4;
	data.push_back(myStruct);
	myStruct.num = 7;
	data.push_back(myStruct);
	myStruct.num = 16;
	data.push_back(myStruct);
	//Merge sort
	MergeSort(data.begin(), data.end(), Max<MyStruct>);
	for (size_t i = 0; i < data.size(); i++)
	{
		cout << data[i].num << ' ';
		cout << endl;
	}
}

3. Output results

General binary search supporting STL

1. Let's create a header file, algorithm search. H. The following is the content

template<class Iterator, class Strategy, class T>
inline Iterator BinarySearch(Iterator _First, Iterator _Last, Strategy _Strategy, const T& key)
{
	Iterator first = _First;
	Iterator end = _Last - 1;
	Iterator mid;
	while (first <= end)
	{
		mid = first + distance(first, end) / 2;
		if (_Strategy(*mid, key) > 0)
			end = mid - 1;
		else if (_Strategy(*mid, key) < 0)
			first = mid + 1;
		else
			return mid;
	}
	return _Last;
}

2. The following is the calling procedure, which extends the binary search based on the original merge sorting. Because binary search needs an ordered set!

#include "stdafx.h"
#include <iostream>
#include "algorithm_sort.h"
#include <stdlib.h>
#include "algorithm_search.h"
using namespace std;
struct MyStruct
{
	int num;
	double age;
};

template<class T>
bool Max(T a, T b)//Sorting strategy
{
	return a.num < b.num;
}

template<class T1, class T2>
int FindKey(T1 a, T2 b)//Search strategy
{
	if (a.num < b)
		return -1;
	if (a.num > b)
		return 1;
	return 0;
}

int _tmain(int argc, _TCHAR* argv[])
{
	MyStruct myStruct;
	myStruct.num = 12;
	myStruct.age = 1.;

	vector<MyStruct> data;
	data.push_back(myStruct);
	myStruct.num = 15;
	data.push_back(myStruct);
	myStruct.num = 9;
	data.push_back(myStruct);
	myStruct.num = 4;
	myStruct.age = 99;
	data.push_back(myStruct);
	myStruct.num = 7;
	myStruct.age = 1.;
	data.push_back(myStruct);
	myStruct.num = 16;
	data.push_back(myStruct);
	//Merge sort
	MergeSort(data.begin(), data.end(), Max<MyStruct>);
	for (size_t i = 0; i < data.size(); i++)
	{
		cout << data[i].num << ' ';
		cout << endl;
	}
	//Two points search
	vector<MyStruct>::iterator it = BinarySearch(data.begin(), data.end(), FindKey<MyStruct, int>, 4);
	cout << it->age << ' ';
	system("PAUSE");
	return 0;
}

3. The output finds the value of age member in the object whose num is 4