unordered series associative containers

unordered_map&& unordered_set

Introduction to relevance container

At the bottom of STL, map and set are implemented in red black tree encapsulation, and their complexity is basically logn, because they are highly controllable, but in the future, a great God came up with another container structure, that is, hash. That is, the bottom layer encapsulates map and set with hash

introduce

1. unordered_map is an associative container for storing < key, value > key value pairs, which allows rapid indexing to their corresponding values through keys.
2. In unordered_ In a map, the key value is usually used to uniquely identify the element, while the mapping value is an object whose content is associated with the key. The types of keys and mapped values may be different.
3. Internally, unordered_map does not sort < Kye, value > in any specific order. In order to find the value corresponding to the key within the constant range, unordered_map places key value pairs of the same hash value in the same bucket.
4. unordered_ The map container accesses a single element through a key faster than a map, but it is usually inefficient in traversing the range iteration of a subset of elements.
5. unordered_maps implements the direct access operator (operator []), which allows direct access to value using key as a parameter.
6. Its iterators are at least forward iterators.
   Note: unordered_ The key in the map cannot be repeated, so the maximum return value of the count function is 1
   Whether unordered_ The usage rules of map / SE are not much different from those of map and set, but the underlying implementation is different. Different efficiency.

Bottom structure

Hash concept

In order structure and balance tree, there is no corresponding relationship between element key and its storage location. Therefore, when looking for an element, it must be compared many times by key. The time complexity of sequential search is O(N), and the height of the tree in the balance tree is O(N). The efficiency of search depends on the comparison times of elements in the search process.

Ideal search method: you can get the elements to be searched directly from the table at one time without any comparison. If a storage structure is constructed to establish a one-to-one mapping relationship between the storage location of an element and its key code through a function (hashFunc), the element can be found quickly through this function.

Insert element:
According to the key of the element to be inserted, this function calculates the storage location of the element and stores it according to this location

Search elements:
Carry out the same calculation for the key of the element, take the obtained function value as the storage location of the element, and compare the elements according to this location in the structure. If the key codes are equal, the search is successful

This method is called hash (hash) method. The conversion function used in hash method is called hash (hash) function, and the structure constructed is called hash table (or Hash list)

For example:
Each time you give a number to take its module, get a value and insert it, which means counting and sorting before.

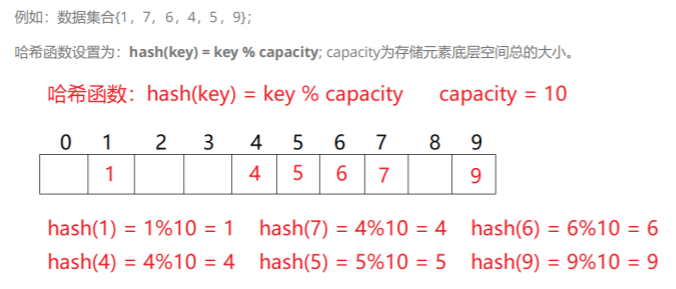
If there are many bad elements, there will inevitably be repeated words.

Hash Collisions

For the same hash address of different keywords, we call this hash conflict.
It is solved by hash function.
Design principle:

1. The definition field of hash function must include all keys to be stored. If the hash table allows m addresses, its value field must be between 0 and m-1
2. The address calculated by hash function can be evenly distributed in the whole space
3. Hash functions should be simple

Common hash functions: direct customization method, division and remainder method, square middle method, folding method, random number method and mathematical analysis method.
The first two are often used

Note: the more sophisticated the hash function is designed, the lower the possibility of hash conflict, but hash conflict cannot be avoided

Closed hash

Introduction to closed hash

Closed hash: also known as open addressing method. In case of hash conflict, if the hash table is not full, it means that there must be an empty position in the hash table, then the key can be stored in the "next" empty position in the conflict position

1. Linear detection
For the conflicting keywords, we perform a linear search, find the corresponding position through the hash function, insert if there is no one, and find an empty position to insert if there is one.

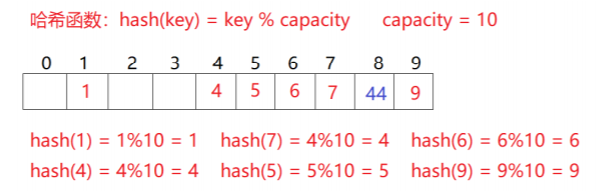
Here, the state of each position of the hash is defined. When using closed hash to deal with hash conflict, the existing elements in the hash table cannot be deleted physically. If the elements are deleted directly, the search of other elements will be affected. For example, if element 4 is deleted directly, 44 searching may be affected. Therefore, linear detection uses the marked pseudo deletion method to delete an element

Capacity expansion mechanism:
When all elements are fully inserted and their states are existing, it is impossible to find the corresponding empty positions and keep the same cycle. Therefore, we should ensure that the closed hash cannot be full or nearly full. When it reaches a certain proportion, we should expand its capacity mechanism.

2. Secondary detection
It can be concluded from one detection that if a large number of data are stacked together in the same area, the efficiency will be reduced, that is, one detection will become a power search

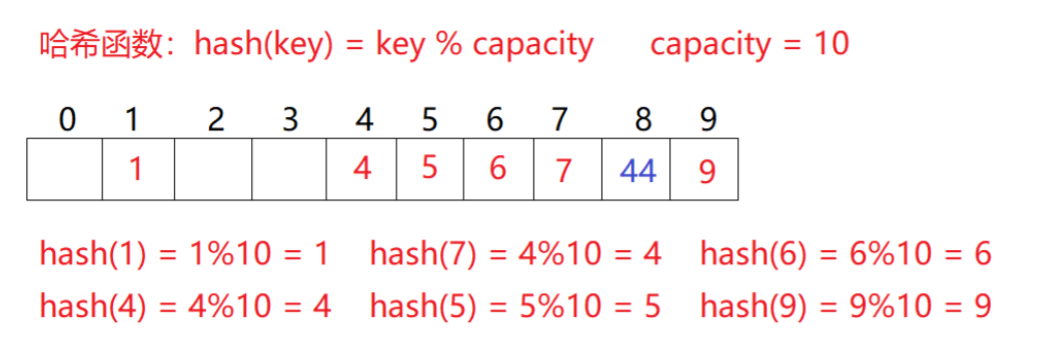
The research shows that when the length of the table is a prime number and the table loading factor A does not exceed 0.5, the new table entry can be inserted, and any position will not be explored twice. Therefore, as long as there are half empty positions in the table, there will be no problem of full table. When searching, you can not consider the situation that the table is full, but when inserting, you must ensure that the loading factor a of the table does not exceed 0.5. If it exceeds, you must consider increasing the capacity.
Low space utilization and hash defects

realization

	enum State
	{
		EXIST,
		EMPTY,
		DELETE,
	};

	template<class T>
	struct HashNode
	{
		State _state = EMPTY; // state
		T _t;
	};

	template<class K, class T, class HashFunc = Hash<K>>
	class HashTable
	{
	public:
		bool Insert(const T& t)
		{
			// If the load factor is > 0.7, the capacity will be increased
			if (_tables.size() == 0 || _size * 10 / _tables.size() == 7)
			{

				size_t newsize = GetNextPrime(_tables.size());


				HashTable<K, T> newht;
				newht._tables.resize(newsize);
				for (auto& e : _tables)
				{
					if (e._state == EXIST)
					{
						// Reuse the logic of conflict detection
						newht.Insert(e._t);
					}
				}

				_tables.swap(newht._tables);
			}

			HashNode<T>* ret = Find(t);
			if (ret)
				return false;


			size_t start = t % _tables.size();
			// Linear detection, find an empty position
			size_t index = start;
			size_t i = 1;
			while (_tables[index]._state == EXIST)
			{
				index = start + i;
				index %= _tables.size();

				++i;
			}

			_tables[index]._t = t;
			_tables[index]._state = EXIST;
			_size++;

			return true;
		}

If a string is passed in, we need to convert it into ASC | code for calculation. We need to introduce an imitation function to specialize a structure. If a string is passed in, we need to de specialize it.

template<class K>
struct Hash
{
	size_t operator()(const K& key)
	{
		return key;
	}
};

// Specialization
template<>
struct Hash < string >
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (auto ch : s)
		{
			//hash += ch;
			hash = hash * 131 + ch;
		}

		return hash;
	}
};

Of course, searching and deleting are similar: searching for existing and equal values will fail if they are empty. To delete, you must first find and then set the status. When inserting, you should first find it. If there is one, it will fail

Open hash

introduce

The open hash method, also known as the chain address method (open chain method), first uses the hash function to calculate the hash address of the key code set. The key codes with the same address belong to the same subset. Each subset is called a bucket. The elements in each bucket are linked through a single linked list, and the head node of each linked list is stored in the hash table.

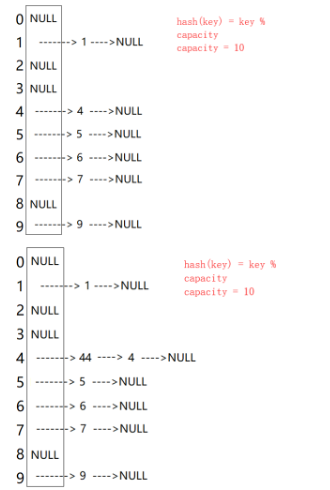
Open hash capacity increasing mechanism

The hashing expansion mechanism will not affect your own insertion. If too many nodes are inserted through a bucket and do not go back, others will only affect your efficiency. The best case is that one node in each bucket does not need secondary search and there will be no hash conflict.

realization

When the size is 0, give the first prime number (the capacity of some prime numbers studied by the great gods here is not easy to conflict), create a new object and reuse its insertion process, insert the points on the old table into the new table one by one, and then release the old table nodes and empty them.

pair<Node*, bool> Insert(const T& t)
		{
			KeyOfT kot;
			// Capacity increase when load factor = = 1
			if (_size == _tables.size())
			{
				size_t newsize = GetNextPrime(_tables.size());
				vector<Node*> newtables;
				newtables.resize(newsize, nullptr);
				for (size_t i = 0; i < _tables.size(); i++)
				{
					// The nodes in the old table are directly removed and hung to the new table
					Node* cur = _tables[i];
					while (cur)
					{
						Node* next = cur->_next;
						size_t index = HashFunc(kot(cur->_t), newtables.size());
						// Head insert
						cur->_next = newtables[index];
						newtables[index] = cur;
						cur = next;
					}
					_tables[i] = nullptr;
				}
				newtables.swap(_tables);
			}
			size_t index = HashFunc(kot(t), _tables.size());
			// t not found
			Node* cur = _tables[index];
			while (cur)
			{
				if (kot(cur->_t) == kot(t))
					return make_pair(cur, false);
				cur = cur->_next;
			}
			Node* newnode = new Node(t);
			newnode->_next = _tables[index];
			_tables[index] = newnode;
			return make_pair(newnode, true);
		}

Comparison of open hash and closed hash

The application of chain address method to deal with overflow requires the addition of link pointer, which seems to increase the storage overhead. In fact, the open address method must maintain a large amount of free space to ensure the search efficiency. For example, the secondary exploration method requires the loading factor a < = 0.7, and the space occupied by the table item is much larger than the pointer, so the chain address method saves storage space than the open address method