1, Basic concepts
You can summarize the basic concepts of DBSCAN with 1, 2, 3 and 4.
One core idea: Based on density
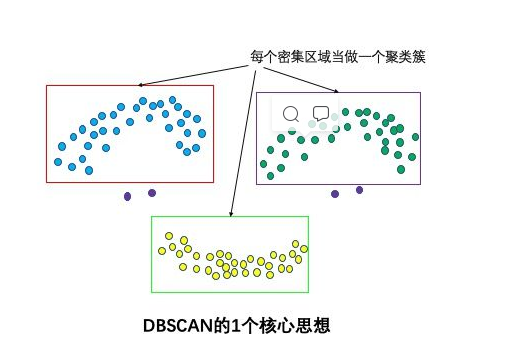
Intuitively, DBSCAN algorithm can find all dense regions of sample points and treat these dense regions as clustering clusters one by one.
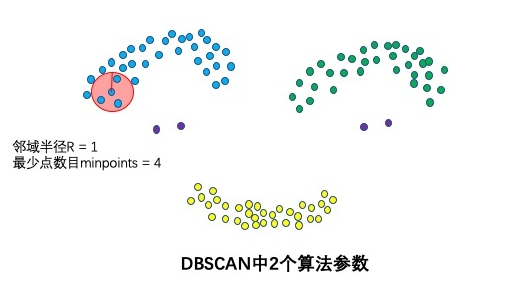
Two algorithm parameters: neighborhood radius R and minimum number of points minpoints
These two algorithm parameters can actually describe what is dense - it is dense when the number of points in the neighborhood radius R is greater than the minimum number of points minpoints.
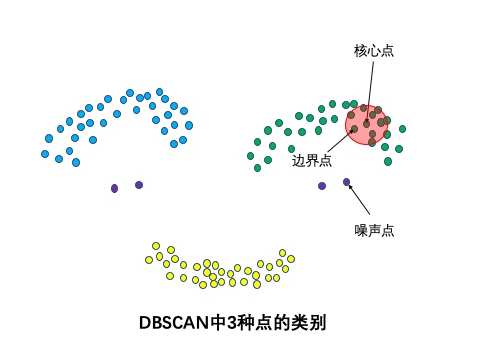
Three types of points: core point, boundary point and noise point
The points where the number of sample points in the neighborhood radius R is greater than or equal to minpoints are called core points. A point that does not belong to a core point but is in the neighborhood of a core point is called a boundary point. Noise points are neither core points nor boundary points.
Four relationships: density direct, density up, density connected, non density connected
If P is the core point and Q is in the R neighborhood of P, it is called density direct from P to Q. Any core point is directly connected to its own density, and the density direct does not have symmetry. If P is directly connected to Q, then q is not necessarily directly connected to P.
If there are core points P2, P3,..., Pn, and the density from P1 to P2 is direct, the density from P2 to P3 is direct,..., the density from P (N1) to Pn is direct, and the density from Pn to q is direct, then the density from P1 to Q can be reached. The density is reachable and has no symmetry.
If there is a core point S so that the density from S to P and Q can be reached, P and Q are connected. Density connection has symmetry. If P and Q are density connected, Q and P are also density connected. Two points connected by density belong to the same cluster.
If the two points do not belong to the density connection relationship, the two points are not density connected. Two non density connected points belong to different clusters, or there are noise points in them.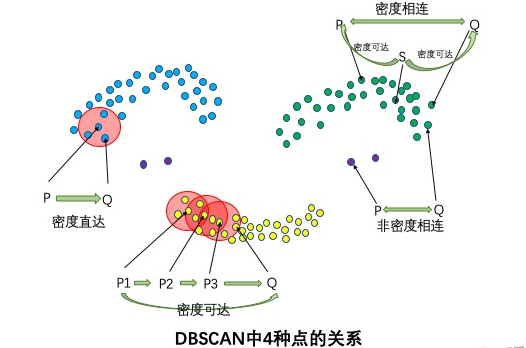
II. Algorithm description
The definition of cluster in DBSCAN algorithm is very simple. The maximum density connected sample set derived from the density reachability relationship is a cluster of the final cluster.
The cluster of DBSCAN algorithm can have one or more core points. If there is only one core point, other non core point samples in the cluster are in the Eps neighborhood of the core point. If there are multiple core points, there must be another core point in the Eps neighborhood of any core point in the cluster, otherwise the density of these two core points cannot be reached. The set of all samples in the Eps neighborhood of these core points constitutes a DBSCAN cluster.
The DBSCAN algorithm is described below.
Input: dataset, neighborhood radius Eps, number of data objects in neighborhood, threshold MinPts;
Output: density connected cluster.
The processing flow is as follows.
1) Select any data object point p from the data set;
2) If the selected data object point p is the core point for the parameters Eps and MinPts, find all the data object points up to the density of p to form a cluster;
3) If the selected data object point p is an edge point, select another data object point;
4) Repeat steps (2) and (3) until all points are processed.
The computational complexity of DBSCAN algorithm is O(n) ²), N is the number of data objects. This algorithm is sensitive to the input parameters Eps and MinPts.
The code implementation logic is as follows:
1) Calculate the number of points pts within the eps range of each point;
2) All PTS > minpts points are recorded as core points;
3) For all corepoint s, add the core point subscript within its eps range to the vector set (vector < int > neighbor coreidx);
4) Traverse all corepoint s, and traverse its neighbor coreidx set in a depth first manner, so that the interconnected core point s have the same cluster number;
5) All points with pts < Minpts and within the Core point range are recorded as Borderpoint;
If a Borderpoint is within the eps range of a Core point, make the cluster number of the Borderpoint equal to the cluster number of the Core point;
6) The remaining points are noise points;
The program is over.
3, Code implementation
I read the code of several other blogs, but I feel very messy. Some run incorrectly, or the display effect is poor. I sorted out a code that can be used and displayed, running without error! Added a lot of notes to help understand, easy to understand!
/*
DBSCAN Algorithm
@author:TheQuiteSunshine
*/
#include <iostream>
#include <sstream>
#include <fstream>
#include <vector>
#include <ctime>
#include <cstdlib>
#include <limits>
#include <cmath>
#include <map>
using namespace std;
//In order to visually display the effect of the algorithm, OpenCV library is introduced.
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace cv;
/*
* @Sample point type
*-- The points where the number of sample points in the neighborhood radius R is greater than or equal to minpoints are called core points.
*-- A point that does not belong to a core point but is in the neighborhood of a core point is called a boundary point.
*-- Noise points are neither core points nor boundary points.
*/
enum ESampleType
{
NOISE = 1,
BORDER = 2,
CORE = 3,
};
struct point
{
public:
float x;
float y;
int cluster = 0; //Category (an identification code. Samples belonging to the same category have the same cluster)
//The points where the number of sample points in the neighborhood radius R is greater than or equal to minpoints are called core points.
//A point that does not belong to a core point but is in the neighborhood of a core point is called a boundary point. Noise points are neither core points nor boundary points
int pointType = NOISE; // 1:noise 2:border 3:core (the initial default is noise point)
int pts = 0; //points in MinPts (number of sample points in the specified field)
vector<int> neighborCoreIdx; //For all corepoint s, add the core point subscript within its eps range to vector < int > neighbor coreidx
int visited = 0; //Has it been traversed and accessed
point()
{
}
point(float a, float b)
{
x = a;
y = b;
//cluster = c;
}
};
float stringToFloat(string i)
{
stringstream sf;
float score = 0;
sf << i;
sf >> score;
return score;
}
//Read the text file and parse the data from it.
vector<point> openFile(const char *dataset)
{
fstream file;
file.open(dataset, ios::in);
if (!file)
{
cout << "Open File Failed!" << endl;
vector<point> a;
return a;
}
vector<point> data;
int i = 1;
while (!file.eof())
{
string temp;
file >> temp;
int split = temp.find(',', 0);
point p(stringToFloat(temp.substr(0, split)), stringToFloat(temp.substr(split + 1, temp.length() - 1)));
data.push_back(p);
}
file.close();
cout << "successful!" << endl;
return data;
}
//Calculate the distance between two points in the plane
float squareDistance(point a, point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
/** @brief DBSCAN clustering algorithm
@param dataset: Input sample data [in][out] parameters
@param Eps: Domain radius
@param MinPts: Subscript of cluster center
@return : Returns the category of each sample. The category starts from 1. 0 means unclassified or failed to classify
*/
void DBSCAN(vector<point> &dataset, float Eps, int MinPts)
{
int count = 0;
int len = dataset.size();
//calculate pts
cout << "Calculate the number of neighborhoods of each point" << endl;
for (int i = 0; i < len; i++)
{
//Special attention!!! Here, if j starts from i, it indicates that the number of samples in the neighborhood of a point includes itself. If j starts from i+1, it does not include itself.
for (int j = i; j < len; j++)
{
if (squareDistance(dataset[i], dataset[j]) < Eps)
{
dataset[i].pts++;
dataset[j].pts++;
}
}
}
//Core point: if the number of points of a point within its domain Eps > = minpts, the point is called core point
cout << "Find the core point" << endl;
//Core point set index (the index is the original index of sample points, starting from 0)
vector<int> corePtInxVec;
for (int i = 0; i < len; i++)
{
if (dataset[i].pts >= MinPts)
{
dataset[i].pointType = CORE;
dataset[i].cluster = (++count);
corePtInxVec.push_back(i);
printf("sample(%.1f, %.1f)The number of neighborhood points is:%d,Established as the core point, cluster: %d\n", dataset[i].x, dataset[i].y, dataset[i].pts, dataset[i].cluster);
}
}
//Merge core point s
cout << "Merge core points" << endl;
for (int i = 0; i < corePtInxVec.size(); i++)
{
for (int j = i + 1; j < corePtInxVec.size(); j++)
{
//For all corepoint s, add the core point subscript within its eps range to the vector < int > corepts
if (squareDistance(dataset[corePtInxVec[i]], dataset[corePtInxVec[j]]) < Eps)
{
dataset[corePtInxVec[i]].neighborCoreIdx.push_back(corePtInxVec[j]);
dataset[corePtInxVec[j]].neighborCoreIdx.push_back(corePtInxVec[i]);
printf("Core point%.1f, %.1f)And core points%.1f, %.1f)Within the radius, they are connected to each other and can be merged\n",
dataset[corePtInxVec[i]].x, dataset[corePtInxVec[i]].y, dataset[corePtInxVec[j]].x, dataset[corePtInxVec[j]].y);
}
}
}
//For all corepoint s, the depth first method is adopted to traverse all corepts of each core point, so that the interconnected core points have the same cluster number
for (int i = 0; i < corePtInxVec.size(); i++)
{
for (int j = 0; j < dataset[corePtInxVec[i]].neighborCoreIdx.size(); j++)
{
int idx = dataset[corePtInxVec[i]].neighborCoreIdx[j];
dataset[idx].cluster = dataset[corePtInxVec[i]].cluster;
}
}
//A point that does not belong to a core point but is in the neighborhood of a core point is called a boundary point
cout << "Boundary point, add the boundary point to the near core point" << endl;
//border point,joint border point to core point
for (int i = 0; i < len; i++)
{
if (dataset[i].pointType == CORE) //Ignore core points
continue;
for (int j = 0; j < corePtInxVec.size(); j++)
{
int idx = corePtInxVec[j]; //Core point index
if (squareDistance(dataset[i], dataset[idx]) < Eps)
{
dataset[i].pointType = BORDER;
dataset[i].cluster = dataset[idx].cluster;
printf("sample(%.1f, %.1f)Is established as a boundary point, cluster: %d\n", dataset[i].x, dataset[i].y, dataset[i].cluster);
break;
}
}
}
cout << "Output results:" << endl;
for (int i = 0; i < len; i++)
{
if (dataset[i].pointType == CORE)
{
printf("CORE: x:%.2f, y:%.2f cluster:%d\n", dataset[i].x, dataset[i].y, dataset[i].cluster);
}
else if (dataset[i].pointType == BORDER)
{
printf("BORDER: x:%.2f, y:%.2f cluster:%d\n", dataset[i].x, dataset[i].y, dataset[i].cluster);
}
else
{
printf("NOISE: x:%.2f, y:%.2f cluster:%d\n", dataset[i].x, dataset[i].y, dataset[i].cluster);
}
}
// for(int i=0;i < corePoint.size(); i++)
// {
// clustering<<corePoint[i].x<<","<<corePoint[i].y<<","<<corePoint[i].cluster<<"\n";
// }
}
/*
*@Generate random colors
*/
cv::Scalar random_color()
{
static cv::RNG _rng(10086);
unsigned icolor = (unsigned)_rng;
return cv::Scalar(icolor & 0xFF, (icolor >> 8) & 0xFF, (icolor >> 16) & 0xFF);
}
int main(int argc, char **argv)
{
//Load data
vector<point> dataset = openFile("dataset.txt");
float radius = 2.0; //Neighborhood radius R
int MinPts = 2; //The points whose number of sample points in the neighborhood radius R is greater than or equal to minpoints are called core points
//DBSCAN algorithm for clustering
DBSCAN(dataset, radius, MinPts);
//Six different colors are set
const int colorCnts = 6;
cv::Scalar colors[] = {cv::Scalar(255, 100, 80), cv::Scalar(0, 255, 0), cv::Scalar(0, 0, 255),
cv::Scalar(0, 255, 255), cv::Scalar(255, 0, 255), cv::Scalar(255, 255, 0)};
//Draw the distribution map of the original data
cv::Point offset(10, 10); //This offset is added to all samples to prevent too close to the origin from affecting the visual display effect
cv::Mat originalMat = cv::Mat::zeros(cv::Size(300, 300), CV_8UC3);
for (size_t i = 0; i < dataset.size(); i++)
{
cv::Point pt = offset + cv::Point(dataset[i].x * 10, dataset[i].y * 10);
cv::circle(originalMat, pt, 2, cv::Scalar(0, 0, 255), 2);
}
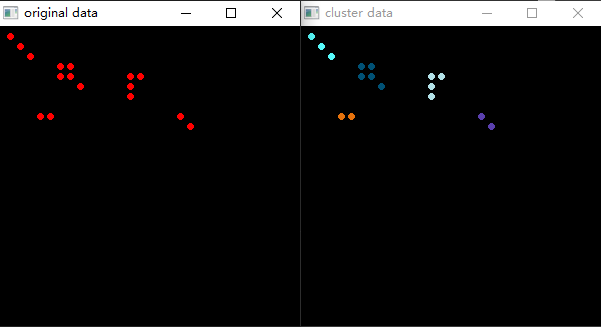
cv::imshow("original data", originalMat);
//Draw the result diagram, and different cluster sample points are represented by different colors.
map<int, cv::Scalar> clusterMap;
map<int, cv::Scalar>::iterator it;
cv::Mat resultMat = cv::Mat::zeros(cv::Size(300, 300), CV_8UC3);
cv::Scalar color;
for (size_t i = 0; i < dataset.size(); i++)
{
it = clusterMap.find(dataset[i].cluster);
if (it == clusterMap.end()) //For the first time, randomly assign a set of colors to the cluster.
{
color = random_color();
clusterMap.insert(std::make_pair(dataset[i].cluster, color));
}
else
color = it->second;
cv::Point pt = offset + cv::Point(dataset[i].x * 10, dataset[i].y * 10);
cv::circle(resultMat, pt, 2, color, 2);
}
cv::imshow("cluster data", resultMat);
cv::waitKey(0);
getchar();
return 0;
}
The dataset used by the attachment Txt file:
0,0 3,8 2,2 1,1 5,3 4,8 6,3 5,4 6,4 7,5 12,4 12,5 12,6 13,4 17,8 18,9
4, Code running effect
5, References
Thanks:
Clustering algorithm DBSCAN-C + + implementation_ k76853 column - CSDN blog_ c++ dbscan