Title Description

The labyrinth consists of N rows of M-column cells (n,m are less than 50), each of which is either empty or obstructed.

1 for open space 2 for obstacles

Now please find a shortest path length from start to end

Input Format

The first row input n,m means there are n rows and m columns

Next, type 1 and 2 for open space and obstacles, respectively

Finally, enter the coordinates of the start and end points

Output Format

Output Shortest Path Length from Start to End

sample input

5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3

sample output

7

Solution 1 (DFS)

Algorithms:

1. Search for a new node from the start in the order of right, bottom, left and top

2. Mark the new node as visited, repeat the first step from this node, and mark the node you just visited as not visited (required for backtracking)

3. When you reach the end point, go back.

Note: After the new node has been accessed and traversed, mark the node as not visited.

#include<cstdio>
using namespace std;
int m,n,endx,endy,min=999;
int a[100][100];//1 for open space 2 for obstacles 
int v[100][100];//0 means no access 0 means access 
int dx[4]={0,1,0,-1};//Four directions, right, bottom, left, top 
int dy[4]={1,0,-1,0};
void DFS(int x,int y,int step)
{
	if(x==endx&&y==endy)
	{
		if(step<min)
			min=step;
		return;
	}
	//Search clockwise in order from bottom right to top left
	for(int k=0;k<=3;k++)
	{
		int tx,ty;
		tx=x+dx[k];
		ty=y+dy[k];
		if(a[tx][ty]==1&&v[tx][ty]==0)
		{
			v[tx][ty]=1;
			DFS(tx,ty,step+1);
			v[tx][ty]=0;
		}
	}
}
int main()
{
	int startx,starty;
	scanf("%d%d",&m,&n);
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&a[i][j]);//1 for open space 2 for obstacles  
		}
	}
	scanf("%d%d%d%d",&startx,&starty,&endx,&endy);
	v[startx][starty]=1;
	DFS(startx,starty,0);
	printf("%d",min);
	return 0;
}

Solution 2 (BFS)

algorithm

1. Enter the starting point into the team

2. Queue entry with movable points at the head of the queue

Queue the first node if there is no point to move

3. When looking for movable nodes, join the team in the order of right, bottom, left and top

Note: Set each node as a structure

* Visited points cannot be accessed again

 

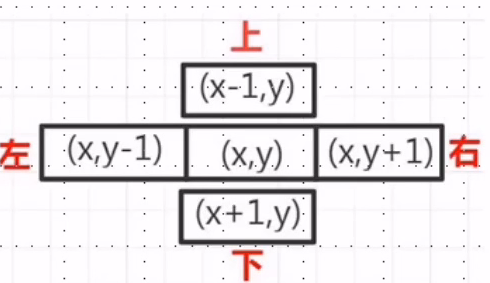
The above figure is an example

Initially in the queue (x,y,step)

(1,1,0)

When step=1, the starting point is used as the node, all movable points are found to join the queue, and the nodes are queued

(1,2,1)(2,1,1)

When step=2, each point is queued as a node to find moving points and queue nodes

(2,2,2)(3,1,2)

When step=3, the same as the previous step

(2,3,3)(3,2,3)(4,1,3)

When step=4, the same as the previous step

(2,4,4)(5,1,4)

When step=5, the same as the previous step

(3,4,5)(1,4,5)(5,2,5)

When step=6, the same as the previous step

(4,4,6)(5,3,6)

When step=7, the same as the previous step

(4,3,7)

#Include <bits/stdc++. H>//BFS Search 
using namespace std;
int a[100][100];//1 for open space 2 for obstacles  
int v[100][100];//0 means no access 0 means access 
struct point
{
	int x;
	int y;
	int step;
};
queue<point> r;//Application queue 
int dx[4]={0,1,0,-1};//Four directions, right, bottom, left, top 
int dy[4]={1,0,-1,0};
int main()
{
	//input
	int n,m,startx,starty,endx,endy;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&a[i][j]);
		}
	}
	scanf("%d%d%d%d",&startx,&starty,&endx,&endy);//Start and end coordinates 
	//BFS
	point start;//The starting point is the structure type 
	start.x=startx;
	start.y=starty;
	start.step=0; 
	r.push(start);//Enroll starting point 
	v[startx][starty]=1;
	int flag=0;
	while(!r.empty()){
		int x=r.front().x;
		int y=r.front().y;
		if(x==endx&&y==endy)
		{
			flag=1;
			printf("%d",r.front().step);
			break;
		}
		for(int k=0;k<=3;k++)
		{
			int tx,ty;
			tx=x+dx[k];
			ty=y+dy[k];
			if(a[tx][ty]==1&&v[tx][ty]==0)
			{
				//Entry
				point temp;
				temp.x=tx;
				temp.y=ty;
				temp.step=r.front().step+1;
				r.push(temp);
				v[tx][ty]=1;
				 
			}
		}
		r.pop();//After the move is complete, the first element needs to be queued 
	}
	if(flag==0)
	printf("no answer");
	return 0; 
}