C language breakthrough advanced - data storage

1. Introduction to data type

We have already learned the basic data types:

char //Character data type
short //Short 
int //plastic
long //Long integer
long long //Longer shaping
float //Single-precision floating-point 
double //Double precision floating point number

For more details, please refer to this website

In particular, there is a boolean type introduced after c99. You want to use the header file to be introduced

_Bool //(from C99)
#include<stdbool.h>
int main()
{
	_Bool flag = true;
	if (flag)
	{
		printf("hehe\n");
	}
	return 0;
}

For string types, c language is not proprietary, but you can create a string array to store strings

And the amount of storage space they occupy.
Meaning of type:

Use this type to open up the size of memory space (the size determines the scope of use).
How to view memory space.

1.1 basic classification of types:

Shaping:

The reason why the character char is in the integer type is that the ASCII value of the corresponding character is an integer

char
	unsigned char
	signed char
short
	unsigned short [int]
	signed short [int]
int
	unsigned int
	signed int
long
	unsigned long [int]
	signed long [int]
long long
    unsigned long long [int]
	signed long long [int]

Note:

Signed is a signed number and unsigned is an unsigned integer
Generally speaking, int is signed int, and char is signed char under most compilers

Floating point number:

float
double

Construction type / custom type:

Array type []
Structure type struct
 Enumeration type enum
 Union type union

Pointer type

int *pi;
char *pc;
float* pf;
void* pv;

Empty type:

void Represents an empty type (no type)

It is usually applied to the return type, parameter and pointer type of a function.

2. Shaping the storage in memory

How is the data stored in the opened memory

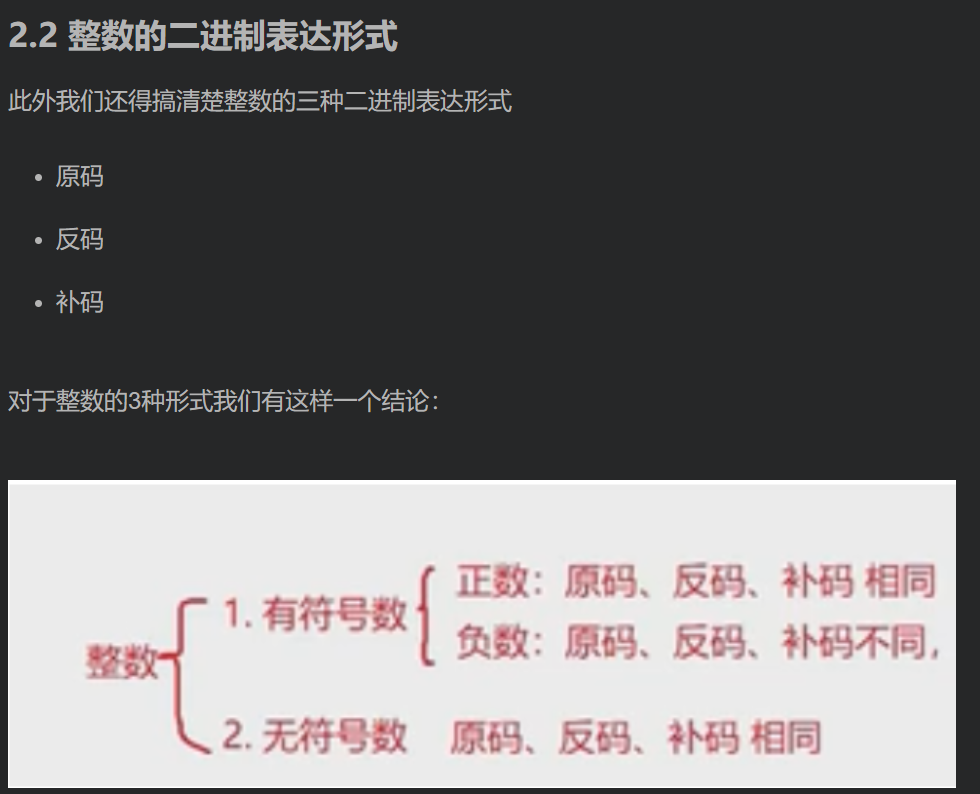
2.1 original code, inverse code and complement code

As mentioned in the operator chapter, there are three storage forms when data is stored in memory

There was a question left before, that is, why should we divide it into these three forms to store it? Isn't it troublesome

Why use complement when storing in memory?

For example, if we want 1-1, we can change it to 1 + (- 1) when there is an adder. When I calculate, if I use the original code

The obtained answer has a problem because of the calculation of the sign bit to i, but if it is calculated with the complement, the negative complement is taken as the inverse

In computer systems, numerical values are always represented and stored by complements. The reason is that the symbol bit and value field can be processed uniformly by using complement; At the same time, addition and subtraction can also be processed uniformly (CPU only has adder). In addition, complement and original code are converted to each other, and the operation process is the same, without additional hardware circuit.

2.2 large end and small end

When a number is accessed in memory, it has its order

In the computer system, we take bytes as the unit, and each address unit corresponds to a byte, one byte is 8bit. When the memory of a data occupies more than one byte, the order of storing data will be reflected.

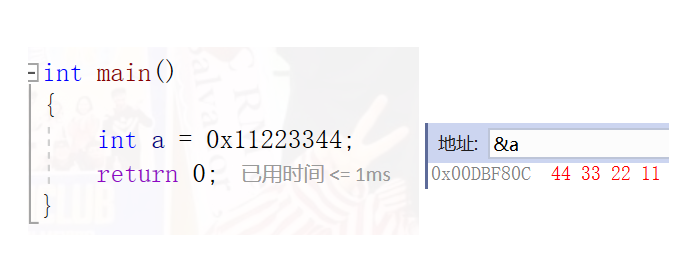
We say that if the order is not specified, the 0x11223344 can be stored in order

Obviously, this is unrealistic

Therefore, it leads to large end storage mode and small end storage mode. So we specify the byte order with large end and small end

Large end byte order:

The low byte data of a data is placed at the high address, and the content of high byte order is placed at the low address. This storage method is called large end byte order

Small end byte order:

The low byte data of a data is placed at the low address, and the content of high byte order is placed at the high address. This storage method is called small end byte order

How can we distinguish intuitively?

You can see how much is stored in the first byte

You can see that if the first byte is 0, it is the big end, and if it is the small end, it is 01

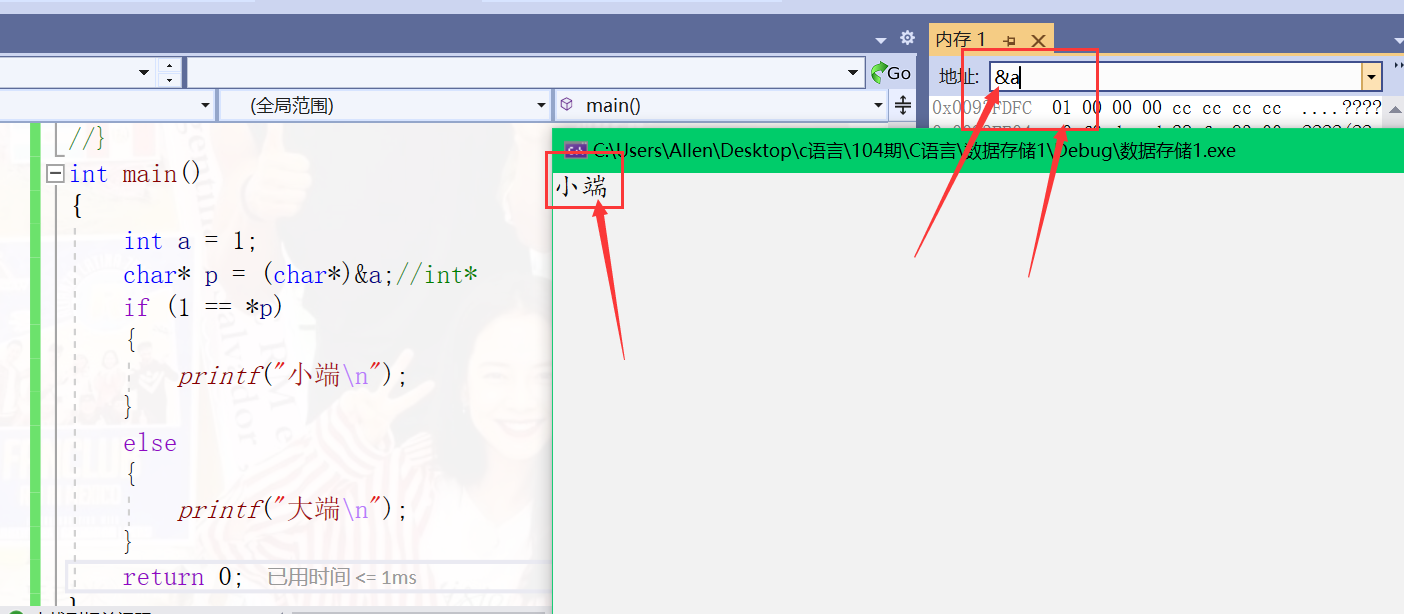
You can see the value of the first byte by using cast

int main()
{
	int a = 0x11223344;
	char* p = (char*)&a;//int*
	if (1 == *p)
	{
		printf("Small end\n");
	}
	else
	{
		printf("Big end\n");
	}
	return 0;
}

It can be seen that VS is the small end

What is the use of such a conclusion? Let's look at it through this topic

2.2.1 a chestnut

Please briefly describe the concepts of large end byte order and small end byte order, and design a small program to judge the byte order of the current machine.

int check_sys()
{
	int a = 1;
	char* p = (char*)&a;
	if (1 == p)
		return 1;
	else
		return 0;
}
int main()
{
	int ret = check_sys();//Return 1 is the small end and return is the large end
	if (1 == ret)
	{
		printf("Small end\n");
	}
	else
	{
		printf("Big end\n");
	}
	return 0;
}

Simplify the function

int check_sys()
{
	int a = 1;
	return *(char*)&a;//p->(char*)&a
}

2.3 A wave of small exercises

A little practice

Chestnut 1

#include <stdio.h>
int main()
{
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,b=%d,c=%d", a, b, c);
	return 0;
}

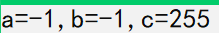
c is special because of the particularity of unsigned

Let's analyze it step by step

First of all, we can know from the debugging that it is the same at the beginning of storage

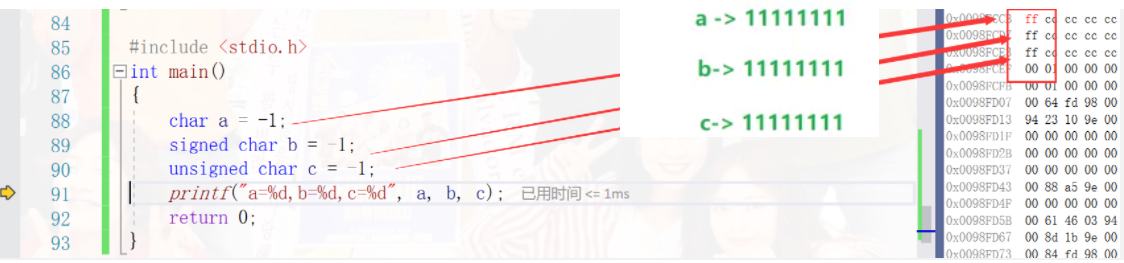
If you want to print, you must improve the integer, that is, according to the original symbol bit

So for signed numbers, printing out is - 1

However, c is unsigned and the high bit is filled with zero, so after 32 bits are filled, it is found that the highest bit is 0, so the original code is the inverse code, and after conversion to the original code is 255

Chestnut 2

#include <stdio.h>
int main()
{
	char a = -128;
	printf("%u\n",a);//Note% u is an unsigned number
	return 0;
}

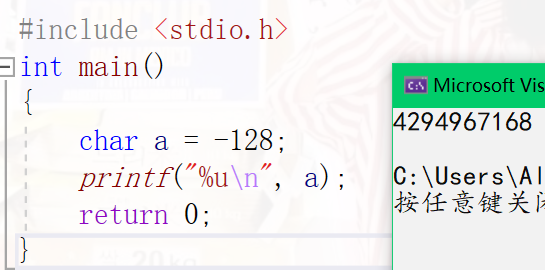
When storing, only 8 bits are taken

A is a signed number, so fill in the high order. After the integer is raised, fill in the highest order 1. Because the unsigned number is output, the last is

Got 4294967168

If so, in fact, a=128 is the same

Chestnut 3

int main()
{
	int i = -20;
	unsigned int j = 10;
	printf("%d\n", i + j);
	return 0;
}

The final output is - 10

Chestnut 4

According to the previous knowledge, why can't the following program stop

int main()
{
	unsigned int i;
	for (i = 9; i >= 0; i--)
	{
		printf("%u\n", i);
	}
	return 0;
}

In fact, VS has intelligently given the reason for the error

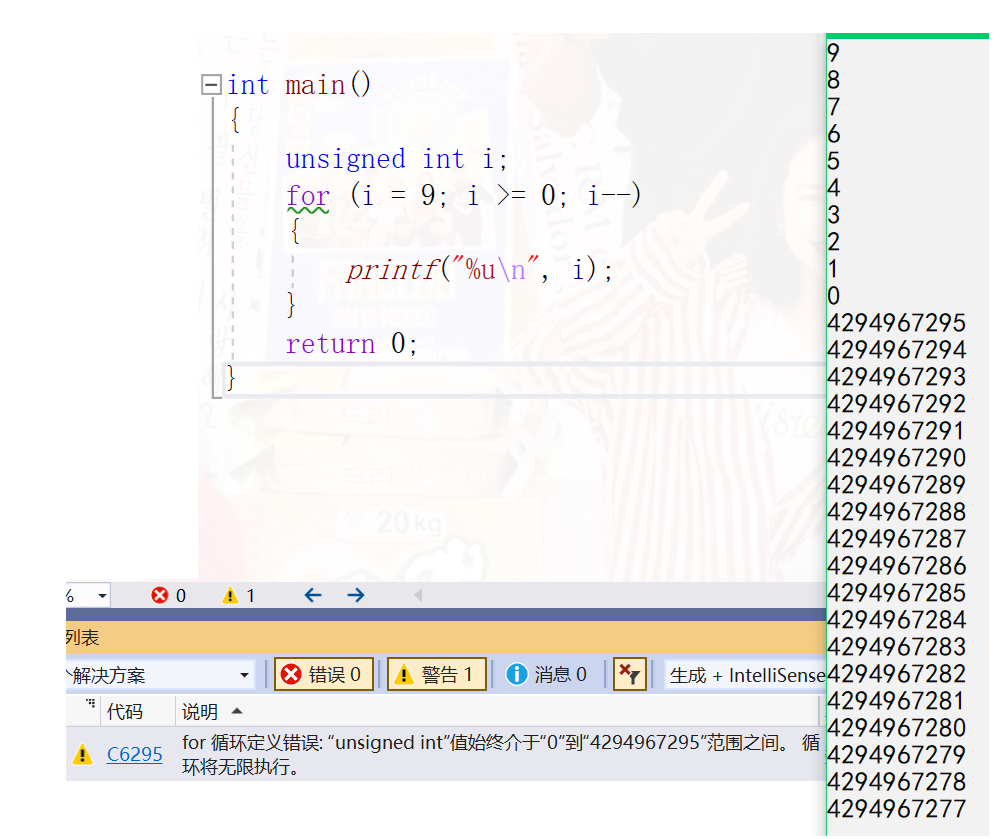
It can never be smaller than 0

Chestnut 6

int main()
{
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

First, we need to know what value a char type variable can put

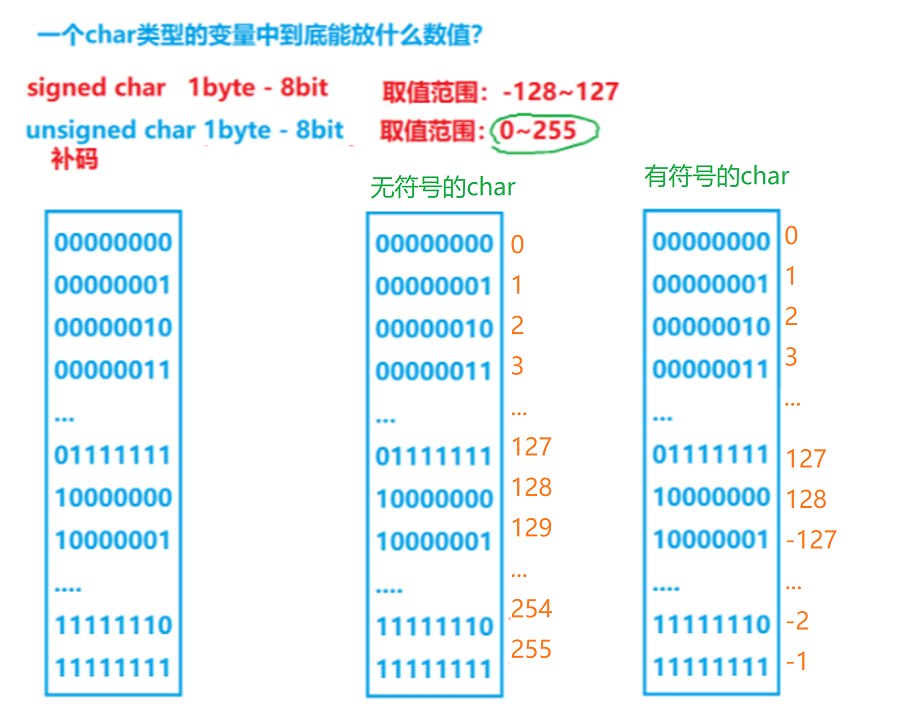
We can turn it into a ⚪ To remember

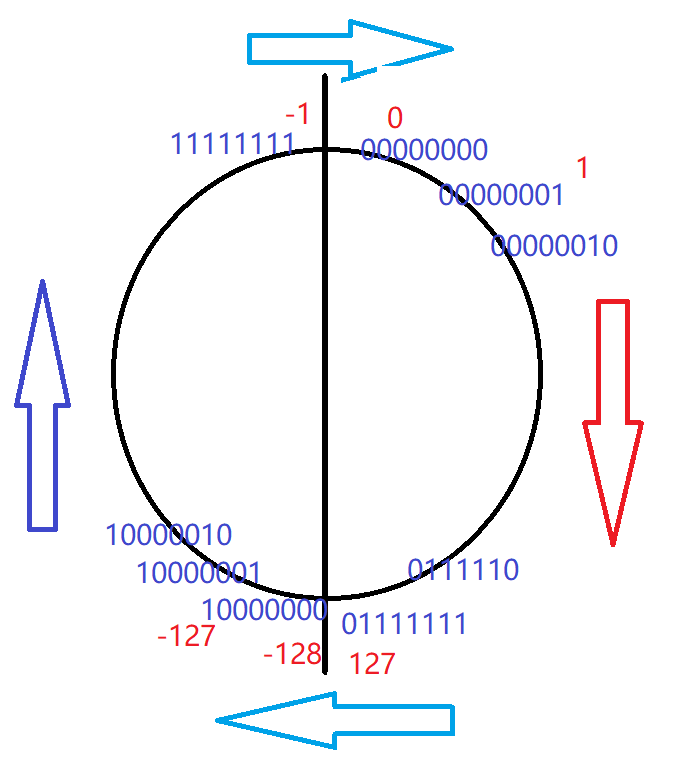
So now let's look at this problem. strlen in the array is required to find \ 0. The number of characters before finding character 0 is 255, that is to say, this ⚪ How many numbers do I have when I walk counterclockwise to 0

Similarly, the signed short is - 32768-32767

There is another way to see the range of these numbers directly

//In this header file
#include<limits.h>
#define CHAR_BIT      8
#define SCHAR_MIN   (-128)
#define SCHAR_MAX     127
#define UCHAR_MAX     0xff
#define MB_LEN_MAX    5
#define SHRT_MIN    (-32768)
#define SHRT_MAX      32767
#define USHRT_MAX     0xffff
#define INT_MIN     (-2147483647 - 1)
#define INT_MAX       2147483647
#define UINT_MAX      0xffffffff
#define LONG_MIN    (-2147483647L - 1)
#define LONG_MAX      2147483647L
#define ULONG_MAX     0xffffffffUL
#define LLONG_MAX     9223372036854775807i64
#define LLONG_MIN   (-9223372036854775807i64 - 1)
#define ULLONG_MAX    0xffffffffffffffffui64

Chestnut 7

#include <stdio.h>
unsigned char i = 0;
int main()
{
		for(i = 0;i<=255;i++)
	{
		printf("hello world\n");
	}
	return 0;
}

Or a dead circle

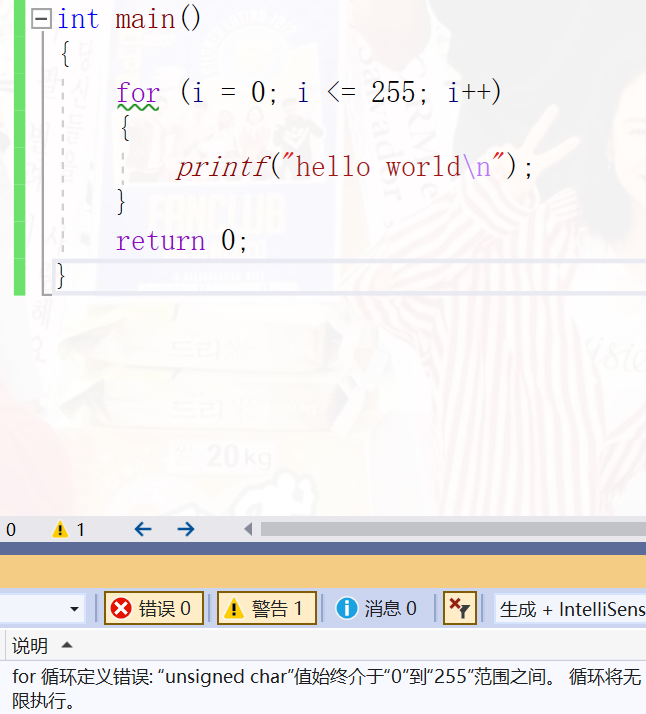
Summary:

When we use unsigned numbers, we'd better pay attention to them

3. Storage of floating point in memory

3.1 introduction

Let's take a look at the particularity of floating-point storage through a chestnut

int main()
{
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n The value of is:%d\n", n);
	printf("*pFloat The value of is:%f\n", *pFloat);
	*pFloat = 9.0;
	printf("num The value of is:%d\n", n);
	printf("*pFloat The value of is:%f\n", *pFloat);
	return 0;
}

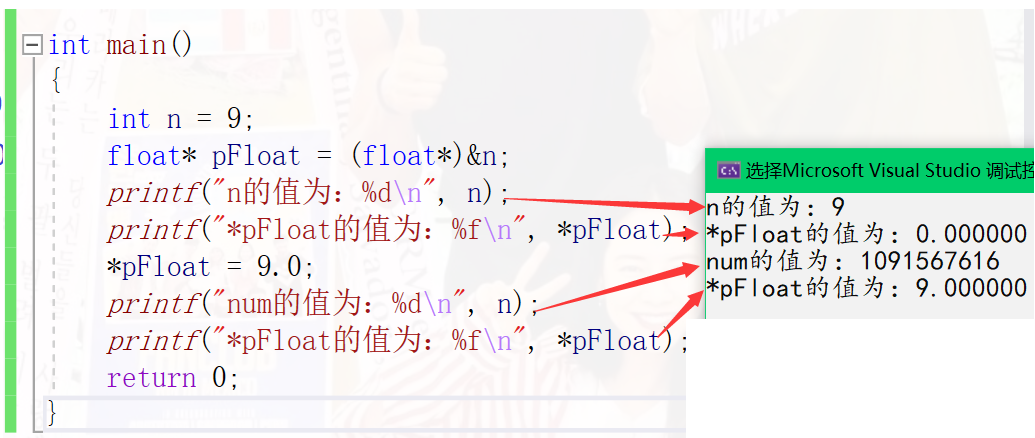
In fact, the problem is that floating-point and integer types are stored in memory in different ways

The third output here is the same. When it is stored in floating-point type and then taken out in integer form, the output value will not be 9

3.2 floating point number storage rules

IEEE standard

According to the international standard IEEE 754, any binary floating-point number V can be expressed in the following form:
( − 1 ) S ∗ M ∗ 2 E (-1)^S * M * 2^E (−1)S∗M∗2E

(- 1)^s represents the sign bit. When s=0, V is a positive number; When s=1, V is negative.
M represents a significant number, greater than or equal to 1 and less than 2.
2^E represents the exponential bit.

For example:

Decimal 5.0, written in binary, is 101.0, equivalent to 1.01 × twenty-two
- Then, according to the above V format, we can get s=0, M=1.01, E=2
Decimal - 5.0, written as binary is - 101.0, equivalent to - 1.01 × twenty-two
- Then, s=1, M=1.01, E=2

IEEE 754 states:
For 32-bit floating-point numbers, the highest 1 bit is the sign bit s, the next 8 bits are the exponent E, and the remaining 23 bits are the significant number M.

For 64 bit floating-point numbers, the highest bit is sign bit S, the next 11 bits are exponent E, and the remaining 52 bits are significant digits M.

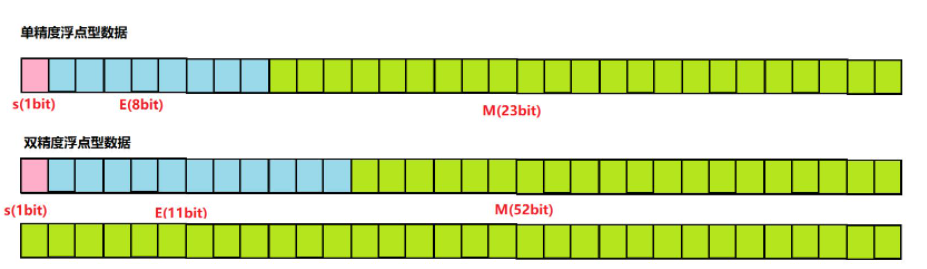
###IEEE 754 has some special provisions on the significant number M and index E

Significant digit M

For m, 1 ≤ m < 2, that is, M can be written in the form of 1.xxxxxx, where XXXXXX represents the decimal part.

IEEE 754 stipulates that when saving M in the computer, the first digit of this number is always 1 by default, so it can be rounded off and only the following xxxxxx part is saved. For example, when saving 1.01, only 01 is saved. When reading, add the first 1. The purpose of this is to save 1 significant digit
- Take the 32-bit floating-point number as an example. There are only 23 bits left for M. after rounding off the 1 of the first bit, it is equivalent to saving 24 significant digits.

Index E, the situation is complex.

First, E is an unsigned integer (unsigned int)

This means that if E is 8 bits, its value range is 0 ~ 255;
If E is 11 bits, its value range is 0 ~ 2047.
- However, we know that E in the scientific counting method can have negative numbers, so IEEE 754 stipulates that the real value of e must be added with an intermediate number when stored in memory. For 8-bit e, the intermediate number is 127; For an 11 bit e, the median is 1023. For example, e of 210 is 10, so when saving as a 32-bit floating-point number, it must be saved as 10 + 127 = 137, that is, 10001001.
In fact, that is to say, if < 0, then add the intermediate number to convert it into an effective number

Index E can be extracted from memory and can be divided into three cases

E is not all 0 or all 1

At this time, the floating-point number is represented by the following rule, that is, subtract 127 (or 1023) from the calculated value of index E to obtain the real value, and then add the first 1 before the significant number M.
For example:
The binary form of 0.5 is 0.1. Since it is specified that the positive part must be 1, that is, the decimal point is shifted to the right by 1 digit, it is
1.0 * 2-1, its order code is - 1 + 127 = 126, expressed as
01111110, and the mantissa 1.0 is 0 after removing the integer part, and 0 to 23 bits 00000000000000000000000 are supplemented, then its binary representation is:

0 01111110 00000000000000000000000

E is all 0

At this time, the exponent E of the floating point number is equal to 1-127 (or 1-1023), which is the real value,
The significant number M is no longer added with the first 1, but is reduced to a decimal of 0.xxxxxx. This is done to represent ± 0 and small numbers close to 0.

######E is all 1

At this time, if the significant digits M are all 0, it means ± infinity (the positive and negative depend on the sign bit s)

Let's explain the previous topic at this time

Answer the previous question:

Look at the first part first

When 0x00000009 is restored to a floating point number, it becomes 0.000000
First, split 0x00000009 to obtain the first sign bit s=0, the index E=00000000 in the following 8 bits, and the last 23 significant digits M = 000 million 1001
Since the index E is all 0, it conforms to the second case in the previous section. Therefore, the floating-point number V is written as:
V=(-1)0 × 0.00000000000000000001001×2(-126)=1.001×2(-146)
Obviously, V is a small positive number close to 0, so it is 0.000000 in decimal
Look at the second part

Floating point number 9.0, how to use binary representation? What is the decimal system?
First, floating point number 9.0 equals binary 1001.0, i.e. 1.001 × 23.

9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130

Then, the sign bit of the first bit s=0, the significant number M is equal to 001, followed by 20 zeros to fill 23 bits, and the index E is equal to 3 + 127 = 130, i.E. 10000001.
So, in binary form, it should be s+E+M, that is
The 32-bit binary number is converted into decimal and printed, which is 1091567616