Stack

Linear tables that allow insert or delete operations only at one end.

1, Introduction to the basic operation of stack

• & InitStack: initialize stack. Construct an empty stack S and allocate memory space.
• Destroy & stack: destroy stack. Destroy and free the memory space occupied by stack S.
• Push & S, X: enter the stack. If stack s is not full, add x to make it called the new stack top.
• Pop & S, & x): out of the stack. If the stack is not empty, the top element of the stack will pop up and return with X.
• Gettop (S, & x): read the top element of stack. If stack S is not empty, use X to return the top element.

2, Implementation of sequential storage of stack

1. Definition of sequence stack

See the following code snippet to understand the definition of sequence stack:

#define MaxSize 10
typedef struct{
    ElemType data[MaxSize];	//Static arrays store elements in the stack
    int top;			//Stack top pointer      
} SqStack;

void testStack(){
    SqStack S;	//Declare a sequential stack (allocate space)
    //.....
}

2. Initialization

//Initialization stack
void InitStack(SqStack &S){
    S.top=-1;	//Initialize stack top pointer
}

//We can also know how to judge whether the stack is empty
bool StackEmpty(SqStack S){
    if(S.top==-1)	//Stack empty
        return true;
    else
        return false;
}

3. Stack operation

//New element stack
bool Push(SqStack &S,ElemType x){
    if(S.top==MaxSize-1)	//Stack full, error reported
        return false;
    S.data[++S.top]=x;	//Add 1 to the pointer first and put the new element on the stack
    return true;
}

4. Stack out operation

Pop up an element at the top of the stack and return it with x:

bool Pop(SqStack &S,ElemType &x){
    if(S.top==-1)	//Stack empty, error reported
        return false;
    x=S.data[S.top];	//The top element of the stack goes out of the stack first (note the order of and pointer changes)
    S.top=S.top-1;	//The pointer is further reduced by 1
    return true;
}

3, Chain storage implementation of stack

The stack using chain storage is called chain stack. Its advantage is that it is convenient for multiple stacks to share storage space and improve its efficiency, and there is no stack overflow. It is usually realized by single linked list, and it is stipulated that all operations are carried out in the header of single linked list.

Now think about it again. In a single linked list, inserting a node after the header is equivalent to the operation of putting elements into the stack, and deleting an element after the header is equivalent to putting elements out of the stack. But the operations of entering and leaving the stack are carried out in the header of the linked list.

queue

1, Definition of queue

We know that the stack is a linear table that only allows insertion or deletion at one end. What about the queue?

A queue is a linear table that can only be inserted at one end and deleted at the other end. Is it very simple to think about this in combination with queuing in daily life~

The following are the basic operations of the queue:

• Initqueue: initialize the queue and construct an empty queue.
• Destroy & queue: destroy the queue. Destroy and free the memory space occupied by queue Q
• Enqueue (& Q, x): join the queue. If queue q is not full, add x to make it a new tail.
• Dequeue (& Q, & x): out of the queue. If queue q is not empty, delete the queue header element and return it with X.

2, Sequential implementation of queue

1. Initialization

#define MaxSize 10 	// Defines the maximum number of elements in the queue
typedef struct {
    ElemType data[MaxSize];	//Storing queue elements in a static array
    int front,rear;	//Head pointer and tail pointer
}SqQueue;

//Initialize queue
void InitQueue(SqQueue &Q){
    //Initially, the head and tail pointer points to 0
    Q.rear=Q.front=0;
}
//Judge whether the queue is empty, that is, the head and tail pointers point to the same element
bool QueueEmpty(SqQueue Q){
    if(Q.rear==Q.front)	//Air condition
        return true;
    else
        return false;
}

2. Team operation

//Join the team
bool EnQueue(SqQueue &Q,ElemType x){
    if(The queue is full)
        return false;	//When the team is full, an error is reported
    Q.data[Q.rear]=x;	//Insert new element at the end of the team
    Q.rear=(Q.rear+1)%MaxSzie	//End of line pointer plus 1 to take mold
}

The operation of judging whether the queue is full in the above program will be discussed later. The modular operation here is actually to map the infinite integer field to the finite integer set {0,1,2,..., MaxSize-1}, and logically turn the storage space into a "ring".

Combined with the circular queue, we can know the condition that the queue is full: the next position of the tail pointer is the opposite head, that is (Q.rear+1)%MaxSize==Q.front)

3. Out of line operation

Only team leader elements can be removed from the team. Delete a queue header element and return it with x

bool DeQueue(SqQueue &Q,ElemType &x){
    if(Q.rear==Q.front)	//Judge team empty
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%MaxSize;	//Queue head pointer moves backward
    return true;
}

How do you know the number of queue elements? Here is a formula. I hope we can remember: (rear + maxsize front)% maxsize. I can verify the legitimacy of this formula.

3, Chain implementation of queue

1. Chain implementation of queue

The code is as follows:

typedef struct LinkNode{	//Chain queue node
    Elemtype data;
    struct LinkNode *next;
}LinkNode;

typedef struct{					//Chain queue
    LinkNode *front,*rear;		//Queue head and tail pointers
}LinkQueue;

Implementation of initialization queue (leading node):

void InitQueue(LinkQueue &Q){
    //Initially, both front and rear point to the head node
    Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
    Q.front->next=NULL;
}
void testLinkQueue(){
    LinkQueue Q;	//Declare a queue
    InitQueue(Q);	//Initialize queue
    //...  Follow up
}

The schematic diagram is as follows:

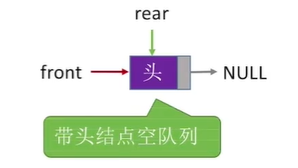
Therefore, the code to judge whether a queue is empty is implemented as follows:

bool IsEmpty(LinkQueue Q){
    if(Q.front==Q.rear)
        return true;
    else
        return false;
}

Queue initialization without leading node:

void InitQueue(LinkQueue &Q){
    //Initially, both front and rear point to NULL
    Q.front=NULL;
    Q.rear=NULL;
}

//At this time, judge whether the queue is empty, that is, the queue head pointer is NULL
bool IsEmpty(LinkQueue Q){
    if(Q.front==NULL)
        return true;
    else
        return false;
}

2. Join the team

The new element joining operation of the leading node only needs to remember that you can only add elements from the end of the queue. The logic is also relatively simple. See the following code snippet directly:

void EnQueue(LinkQueue &Q,ElemType x){
    LinkNode *s=(LinkNode *)mallloc(sizeof(LinkNode));
    s->data=x;
    s->next=NULL;
    Q.rear->next=s;	//After the new node is inserted into the rear
    Q.rear=s;	//Modify footer pointer
}

Do not queue new elements of the leading node. Since the start front and rear pointers point to NULL, they need to be modified:

void EnQueue(LinkQueue &Q,ElemType x){
    LinkNode *s=(LinkNode *)mallloc(sizeof(LinkNode));
    s->data=x;
    s->next=NULL;
    if(Q.front==NULL){	//Inserting the first element into an empty queue requires special processing
        Q.front=s;		//Modify the head and tail pointer
        Q.rear=s;
    }else{
        Q.rear->next=s;	//The new node is inserted after the rear node
        Q.rear=s;	//Modify the real pointer
    }
}

3. Out of the team

The logic of the outgoing operation of the team head element of the leading node is relatively simple. See the code directly:

bool DeQueue(LinkQueue &Q,ElemType &x){
    if(Q.front==Q.rear)
        return false;	//Air force
    LinkNode *p=Q.front->next;
    x=p->data;	//Returns the queue header element with the variable x
    Q.front->next=p->next;	//Modify the next pointer of the header node
    if(Q.rear==p)	//This is the last node out of the team
        Q.rear=Q.front;	//Modify the real pointer
    free(p);	//Free node space
    return true；
}

Do not take the lead node queue header element out of the queue. The code is as follows:

bool DeQueue(LinkQueue &Q,ElemType &x){
    if(Q.front==NULL)
        return false;	//Air force
    LinkNode *p=Q.front;	//p points to the node out of the queue this time
    x=p->data;	//Returns the queue header element with the variable x
    Q.front=p->next;	//Modify the front pointer
    if(Q.rear==p){	//This is the last node out of the team
        Q.front=NULL;	//front points to NULL
        Q.rear=NULL;	//Real points to NULL
    }
    free(p);
    return true;
}

We must try and think more!