Which course does this assignment belong to	https://bbs.csdn.net/forums/csuft_swxy_C?typeId=17321
What are the requirements for this assignment	https://bbs.csdn.net/topics/603700627
The goal of this assignment	< learn new knowledge, practice and consolidate >
Student number	<20218549>

1. Complete PTA homework and give a screenshot of programming questions. The screenshot has its own student number and name identification (0 point if it is not in the form of screenshot)

1.1 Title:

This problem requires the realization of two functions: a function to judge whether the sum of the numbers of a given positive integer is equal to 5; Another function counts how many integers in a given interval meet the above requirements, and calculates the sum of these integers.

Function interface definition:

int is( int number );
void count_sum( int a, int b );

The function is determines whether the sum of the digits of number is equal to 5. If yes, it returns 1, otherwise it returns 0.
Function count_sum uses the function is to count how many integers in a given interval [a, b] meet the above requirements (that is, let is return 1), and calculate the sum of these integers. Finally, according to the format

count = Number of integers satisfying the condition, sum = Sum of these integers

Output. Ensure 0 < a ≤ b ≤ 10000.

Example of referee test procedure:

#include <stdio.h>

int is( int number );
void count_sum( int a, int b );

int main()
{
    int a, b;

    scanf("%d %d", &a, &b);
    if (is(a)) printf("%d is counted.\n", a);
    if (is(b)) printf("%d is counted.\n", b);
    count_sum(a, b);

    return 0;
}

/* Your code will be embedded here */

Input example:

104 999
 No blank lines at the end

Output example:

104 is counted.
count = 15, sum = 3720
 No blank lines at the end

1.1. 1. Map display:

1.1. 2. Data processing:

Data expression: sum is defined to represent the sum of each number, and number represents each number
Data processing: use the function is to judge whether the sum of the numbers of number is equal to 5. If yes, it returns 1, otherwise it returns 0; Count is also used_ Sum function and while loop statement

1.1.3 PTA submission list and Description:

There were many compilation errors before submission because the referee test program sample was copied

1.2 Title:

Narcissus number refers to an n-bit positive integer (n ≥ 3), and the sum of the N powers of the numbers in each bit is equal to itself. For example, 153 = 1 ³+ five ³+ three ³. This problem requires writing two functions, one to judge whether a given integer is the number of daffodils, and the other to print out all the daffodils in a given interval (m,n) from small to large.

Function interface definition:

int narcissistic( int number );
void PrintN( int m, int n );

The narcissistic function determines whether number is the number of daffodils. If yes, it returns 1, otherwise it returns 0.
The function PrintN prints the number of all daffodils in the interval (m, n), and each number occupies one line. Ensure 100 ≤ m ≤ n ≤ 10000.

Example of referee test procedure:

#include <stdio.h>

int narcissistic( int number );
void PrintN( int m, int n );

int main()
{
    int m, n;

    scanf("%d %d", &m, &n);
    if ( narcissistic(m) ) printf("%d is a narcissistic number\n", m);
    PrintN(m, n);
    if ( narcissistic(n) ) printf("%d is a narcissistic number\n", n);

    return 0;
}

/* Your code will be embedded here */

Input example:

153 400

Output example:

153 is a narcissistic number
370
371

1.2. 1. Map display:

1.2. 2. Data processing:

Data expression: integer variables i, sum, a, b, m and N are defined, where sum represents the sum of the corresponding power of each digit number, M represents the digit of the number, n represents the number, and b represents the remainder after number%10.
Data processing: a variety of functions are used. The narcissistic function is used to judge whether number is the number of daffodils. If yes, it returns 1, otherwise it returns 0; The function PrintN prints the number of all daffodils in the interval (m, n), and each number occupies one line. for and while loop statements are also used.

1.2.3 PTA submission list and Description:

Multiple errors: in the defined integer variable, m forgot to initialize

1.3 Title:

This problem requires to realize a simple function to judge prime numbers, and use this function to verify Goldbach's conjecture: any even number not less than 6 can be expressed as the sum of two odd prime numbers. A prime number is a positive integer that can only be divided by 1 and itself. Note: 1 is not prime, 2 is prime.
Function interface definition:

int prime( int p );
void Goldbach( int n );

The function prime returns 1 when the parameter p passed in by the user is a prime number, otherwise it returns 0; The function Goldbach outputs the prime decomposition of N in the format "n=p+q", where p ≤ q are prime numbers. Because such decomposition is not unique (for example, 24 can be decomposed into 5 + 19 and 7 + 17), it is required to output the solution with the smallest P among all solutions.
Example of referee test procedure:

#include <stdio.h>
#include <math.h>

int prime( int p );
void Goldbach( int n );

int main()
{
    int m, n, i, cnt;

    scanf("%d %d", &m, &n);
    if ( prime(m) != 0 ) printf("%d is a prime number\n", m);
    if ( m < 6 ) m = 6;
    if ( m%2 ) m++;
    cnt = 0;
    for( i=m; i<=n; i+=2 ) {
        Goldbach(i);
        cnt++;
        if ( cnt%5 ) printf(", ");
        else printf("\n");
    }

    return 0;
}

/* Your code will be embedded here */

Input example:

89 100
 No blank lines at the end

Output example:

89 is a prime number
90=7+83, 92=3+89, 94=5+89, 96=7+89, 98=19+79
100=3+97, 
No blank lines at the end

1.3. 1. Map display:

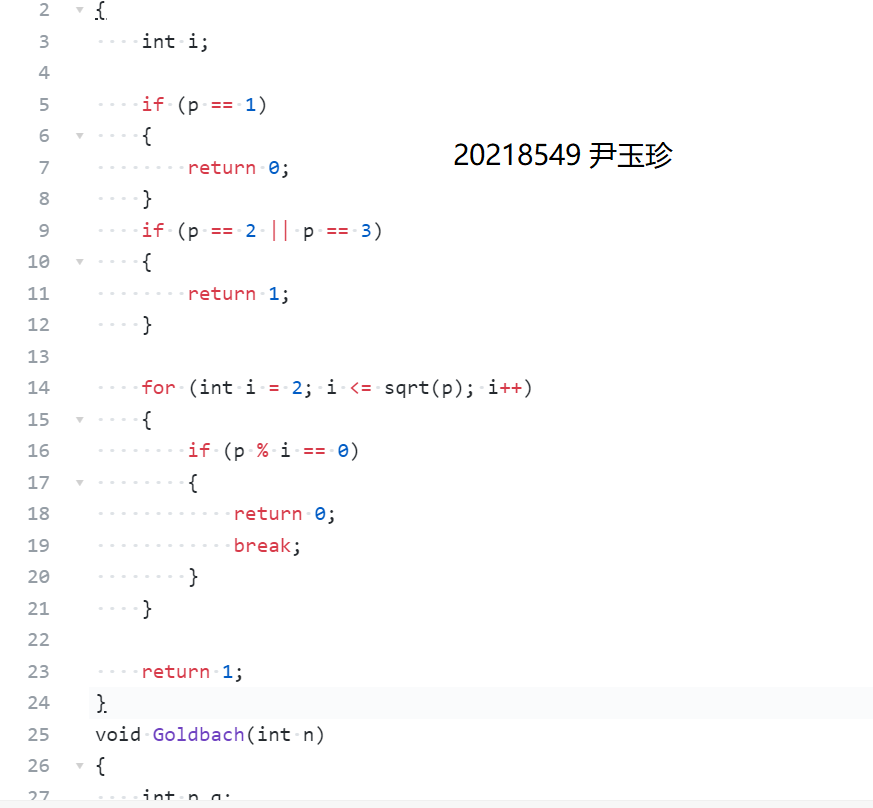
1.3. 2. Data processing:

Data expression: integer variables I, p,q and N are defined, where P and q are prime numbers, where p ≤ q, n is an even number not less than 6, and n=p+q.
Data processing: the function prime indicates that when the parameter p passed in by the user is a prime number, it returns 1, otherwise it returns 0; The function Goldbach represents the prime decomposition of the output number N in the format "n=p+q", where p ≤ q are prime numbers. In addition, the for loop statement and if statement are used.

1.3.3 PTA submission list and Description:

Compilation error: the expression in the for loop statement is written incorrectly;
Format error: i should be initialized before i circulates;
Partial error: p==1 in the first if statement is written incorrectly;

1.4 Title:

Using functions to sum prime numbers

Prime §, where the function prime returns True when the parameter p passed in by the user is a prime number, otherwise it returns false PrimeSum (m, n), the function PrimeSum returns the sum of all primes in the interval [M, n]. The title ensures that the parameter 1 < = m < n passed in by the user.

Function interface definition:

The function interface is described here:
prime(p)，return True express p Is a prime number, return False express p Not prime
PrimeSum(m,n)，Function returns the sum of prime numbers

Example of referee test procedure:

/* Please fill in the answer here */

m,n=input().split()
m=int(m)
n=int(n)
print(PrimeSum(m,n))

Input example:
A set of inputs is given here. For example:

1 10
 No blank lines at the end

Output example:
The corresponding output is given here. For example:

17
 No blank lines at the end

1.4. 1. Map display:

1.4. 2. Data processing:

Data expression: p represents prime, 1 is not prime, 2 is prime, m,n represents interval range, where 1 < = m < n.
Data processing: the function prime returns True when the parameter p passed in by the user is a prime number, otherwise it returns False; The function PrimeSum returns the sum of all primes in the interval [m, n].

1.4.3 PTA submission list and Description:

Non zero return: I didn't pay attention to the Python syntax. I thought it was still C language

***

2.1 learning progress bar**

Week / date	Time spent this week	Code line	Introduction to knowledge learned	At present, there are some confused problems
12.6-12.12	10 hours	130 lines	Use of various functions	Determination of expressions in solving problems

2.2 cumulative code lines and blog words**

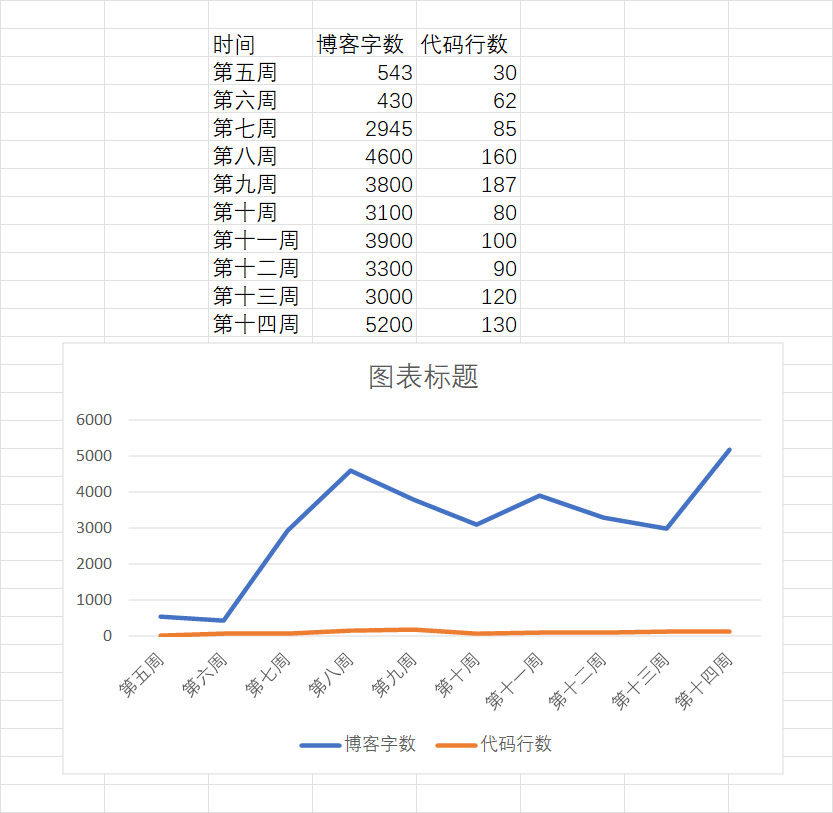
2.3 learning perception**

This week's homework is difficult, especially when you first see the problem, you feel that those functions can't be understood at all, but you find that those functions are very easy to understand. With those functions, the solution to the problem becomes easier. In addition, when you encounter a problem, don't give up without trying. Sometimes it's not particularly difficult to solve the problem later.