preface
Today, we will learn another advanced data structure B tree. We know that the query time complexity of the tree is directly related to the height of the tree. When we insert a large amount of data into the red black tree, there are two problems:
(1) First of all, memory is limited and it is impossible to insert data endlessly. BST based balanced trees such as AVL tree and red black tree are essentially memory based data structures.
(2) Can you store AVL tree, red black tree or jump table directly on disk and then use it for retrieval? The answer is yes, but the problem is that disk based seek query is much slower than memory based query. For example, suppose 1 million data are distributed in red black tree, and the average search performance of red black tree is O (logN) to calculate, when n = 1 million, it takes an average of 20 queries to retrieve any data. If it is in memory, there is no problem at all, but if the red black tree exists on the disk, it is completely different. According to the ordinary hard disk or file system, it takes about 10 milliseconds to query IO every time, so it takes 10 * 2 to retrieve data every time under the amount of millions of data 0, about 0.2 seconds. If the amount of data is expanded 100 times and the total amount of data is 100 million, it takes 20 seconds to retrieve data once. This performance is completely unacceptable. It can be imagined that it is inappropriate to use binary tree in this case.
Because of the problem described, there is an urgent need for a disk or file system friendly data structure, which is B-tree, or extended B +, b * Tree Based on B-tree, etc. The root of the above problem is that the height of the tree is too high, which leads to the query of external memory, that is, too many disk IO accesses, which greatly slows down the retrieval performance. Then the idea is clear. Just find a way to reduce the height of the tree. Yes, B tree is such an m-fork multi-channel balanced tree. You can imagine that its child nodes are as few as 2 and as many as thousands, Therefore, it has changed from the thin height of the binary tree to the short and fat of the multi fork tree. It is in this way that the height of the tree is greatly reduced, making this data structure more suitable for storage on disk, It also makes full use of the read ahead mechanism of disk blocks (principle of local access). The performance is further improved by caching. When a disk reads a file pointer, it usually reads all the data next to it to the cache, because practice has proved that when a file data is accessed, the data around it will also be accessed soon. Here, let's briefly talk about the differences between disk sectors, disk blocks and disks :
Sector: the smallest storage unit of the disk;
Disk block: the smallest unit of data read and written by the file system;
Page: the smallest storage unit of memory;
Generally, the size of disk blocks and pages is 4KB, so the total size of the maximum number of stored data in a node in the B-tree cannot exceed 4KB.
The structure based on B-tree makes full use of this, so it is very suitable for file system or database Index of.
Properties of B-trees
An M-order B-tree T satisfies the following conditions
1. Each node has at most M subtrees
2. The root node has at least two subtrees
3. Except for the root node, each branch node has at least M/2 subtrees
4. All leaf nodes are on the same layer
5. For branch nodes with K sub trees, there are k-1 keywords, which are sorted in ascending order
6. The number of keywords meets ceil (M / 2) - 1 < = n < = M-1
Let's take an example of a B-tree of order 5 (M=5, that is, the inner node except the root node and leaf node has at most 5 children and at least 3 children).
insert operation
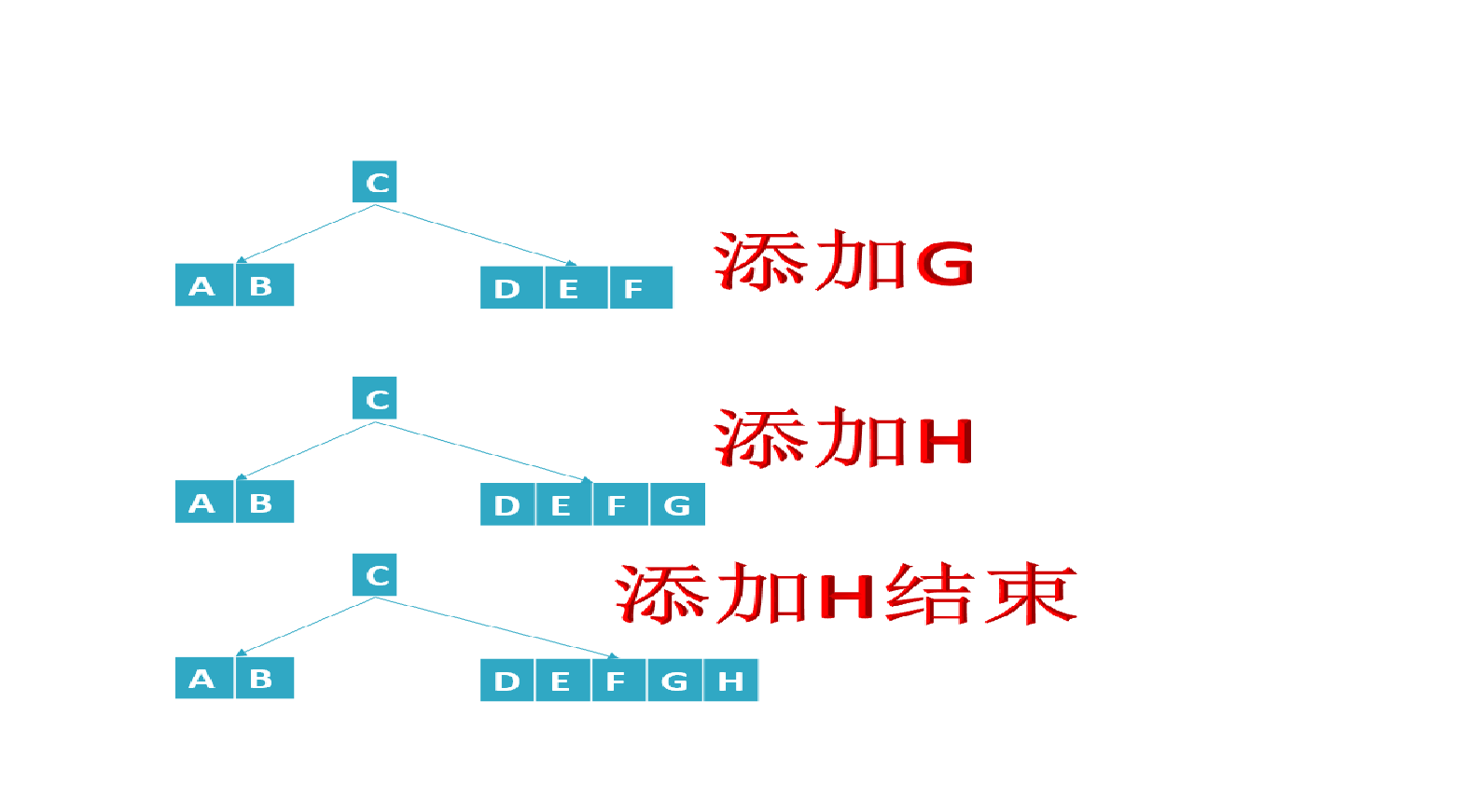
- When inserting an element, first check whether it exists in the B tree. If it does not exist, it ends at the leaf node, and then insert the new element in the leaf node. Note:
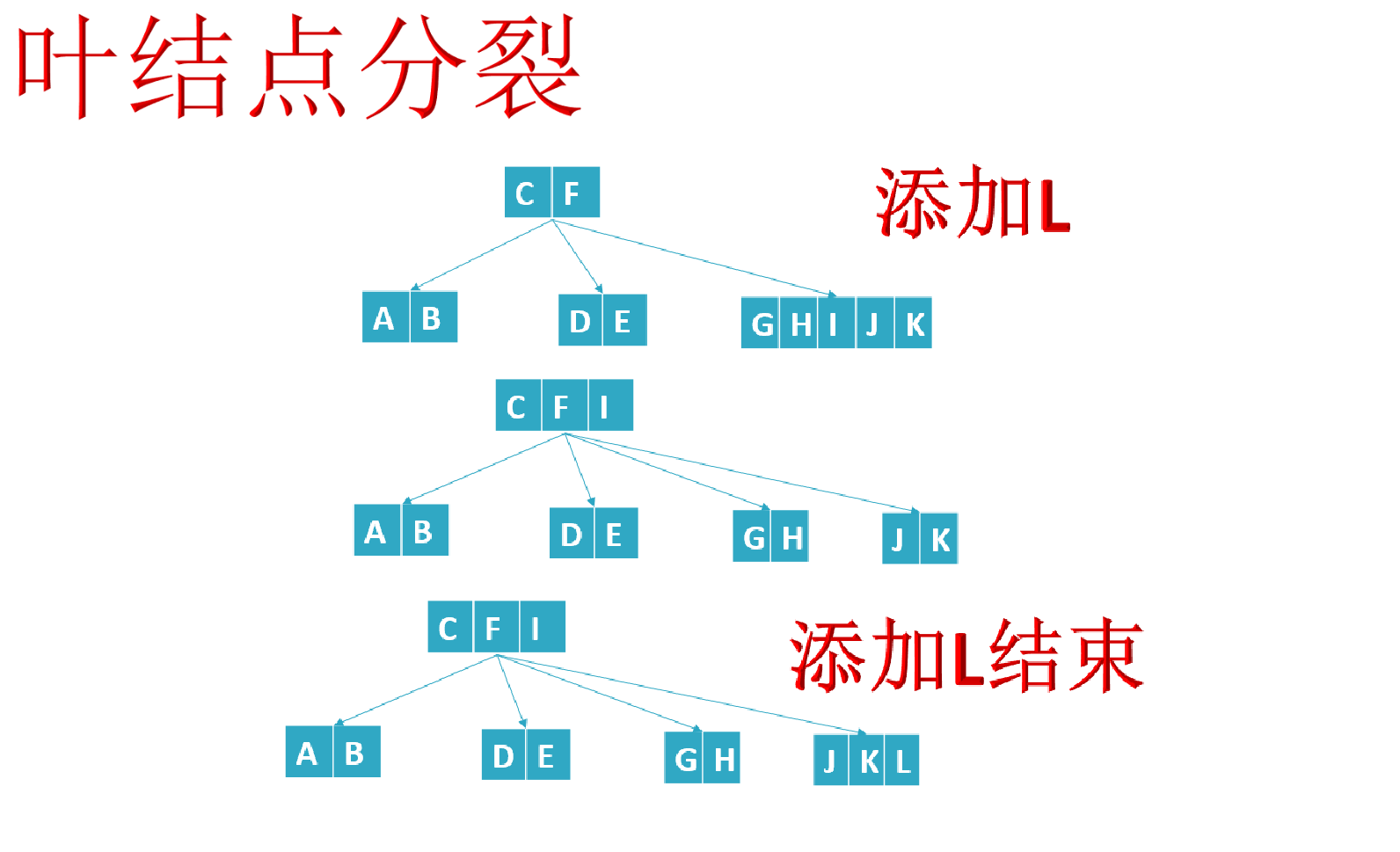
- If the leaf node has enough space, it is necessary to move the element larger than the newly inserted keyword in the leaf node to the right. If the space is full and there is not enough space to add new elements, the node will be "split" and half of the keyword elements will be split into new adjacent right nodes, The intermediate keyword element moves up to the parent node (of course, if the parent node space is full, the "split" operation is also required). Moreover, when the key element in the node moves to the right, the relevant pointer also needs to move to the right.
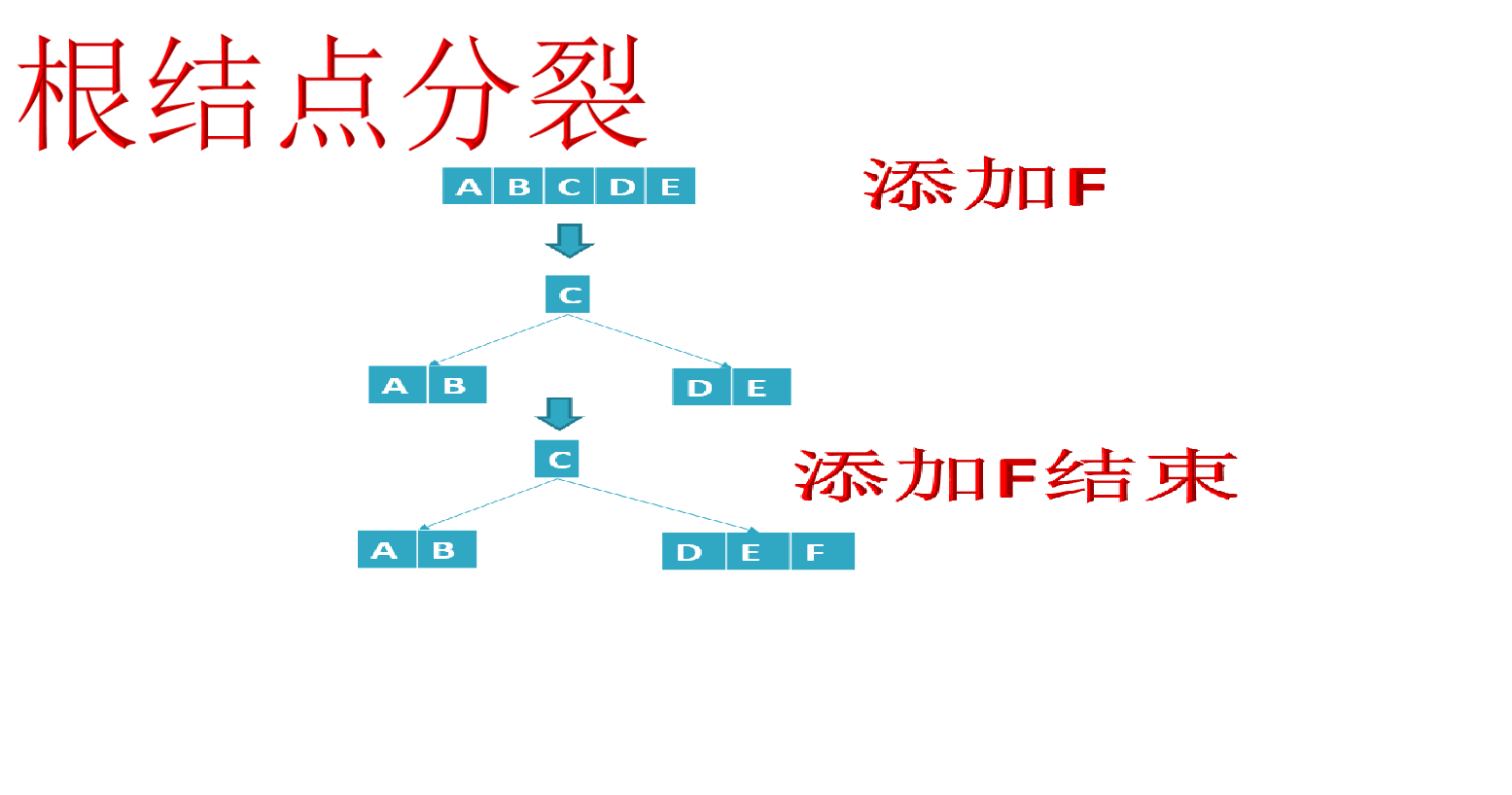
- If a new element is inserted into the root node and the space is full, the splitting operation is carried out, so that the intermediate keyword element in the original root node moves upward to the new root node, resulting in an increase in the height of the tree.
Delete operation
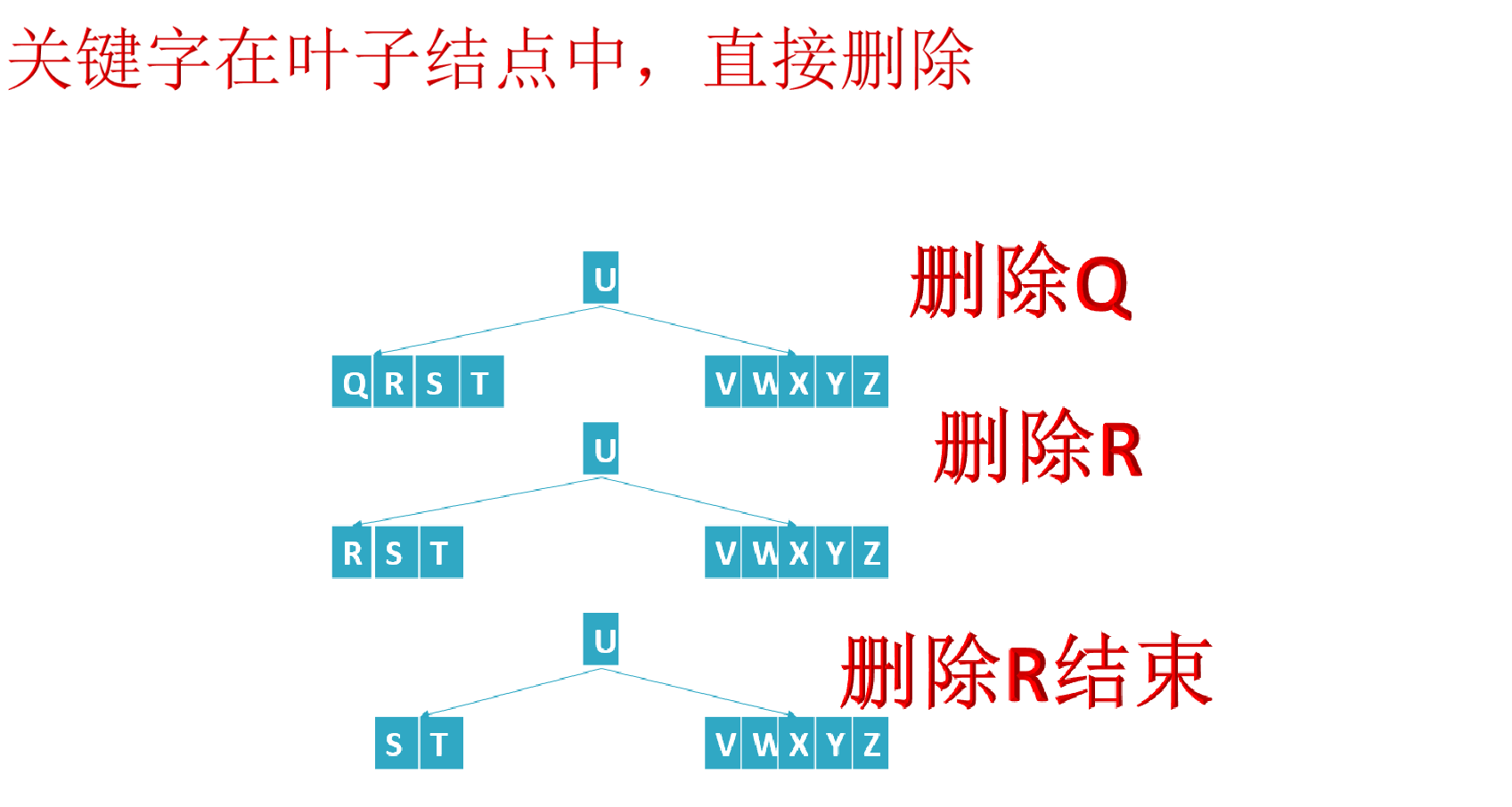
First, find the element to be deleted in the B tree. If the element exists in the B tree, delete the element in its node. If the element is deleted, first judge whether the element has left and right child nodes. If so, move a similar element in the child node up to the parent node, and then move it; If not, go to the situation after direct deletion and after moving.
After deleting the element and moving the corresponding element,
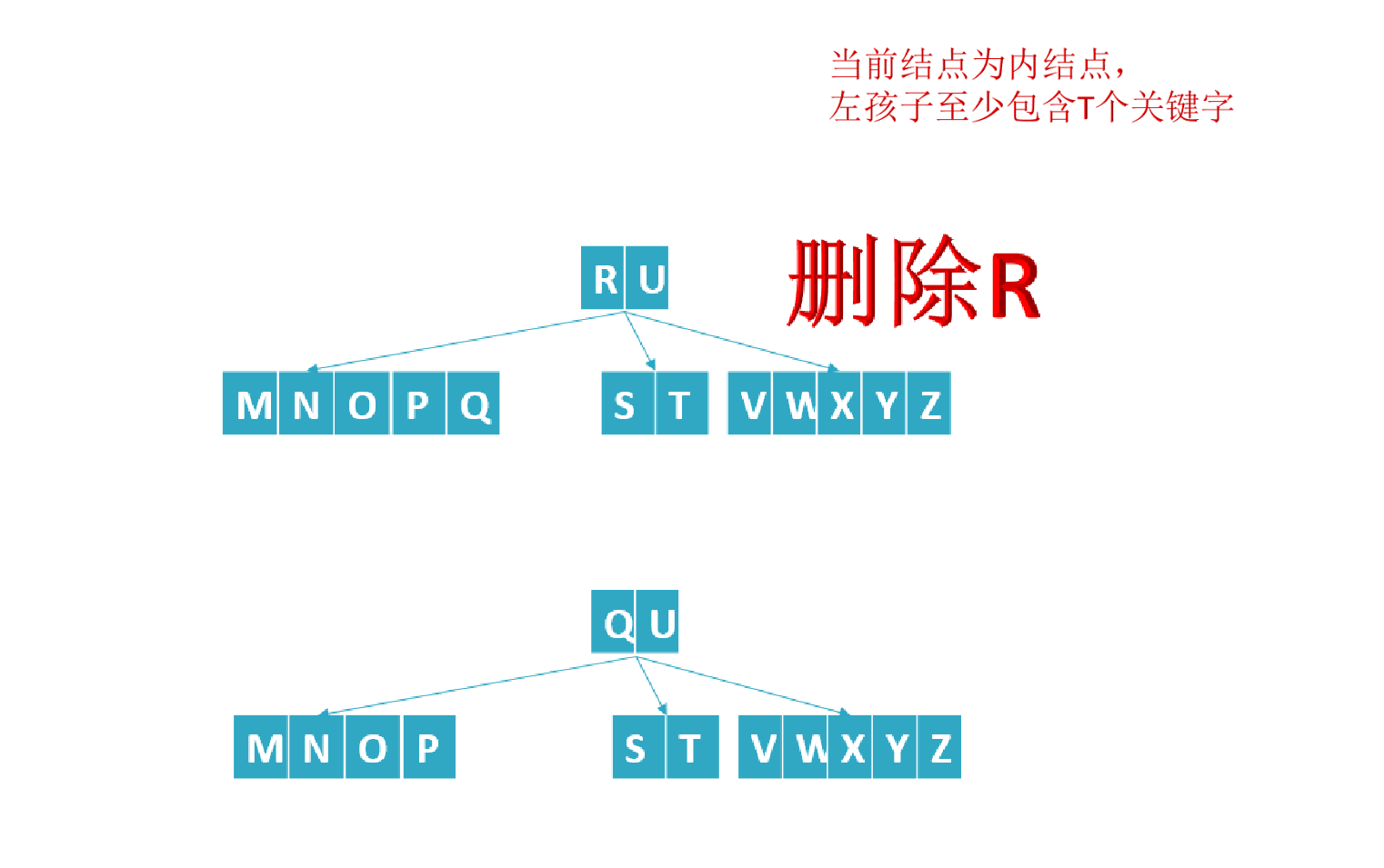
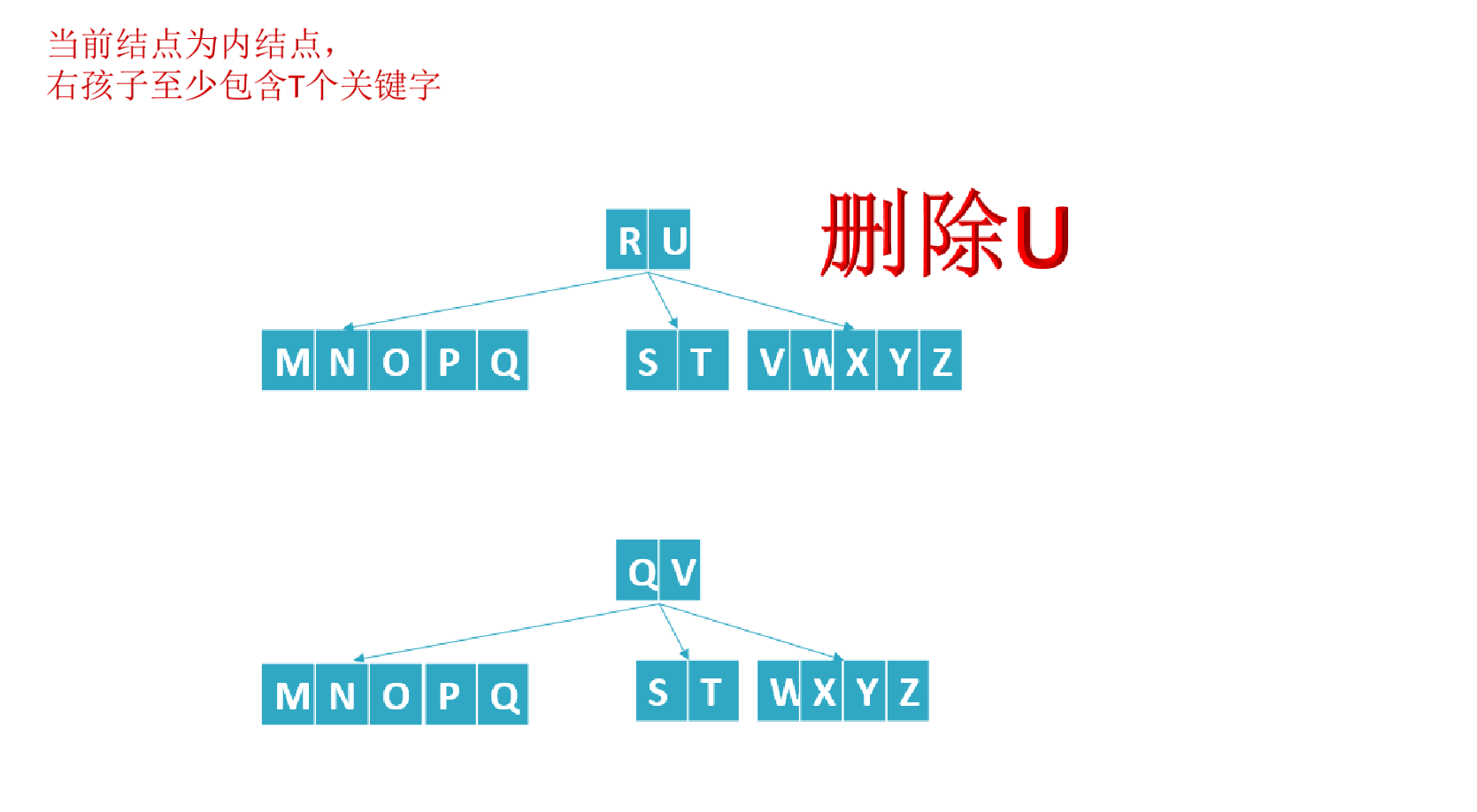
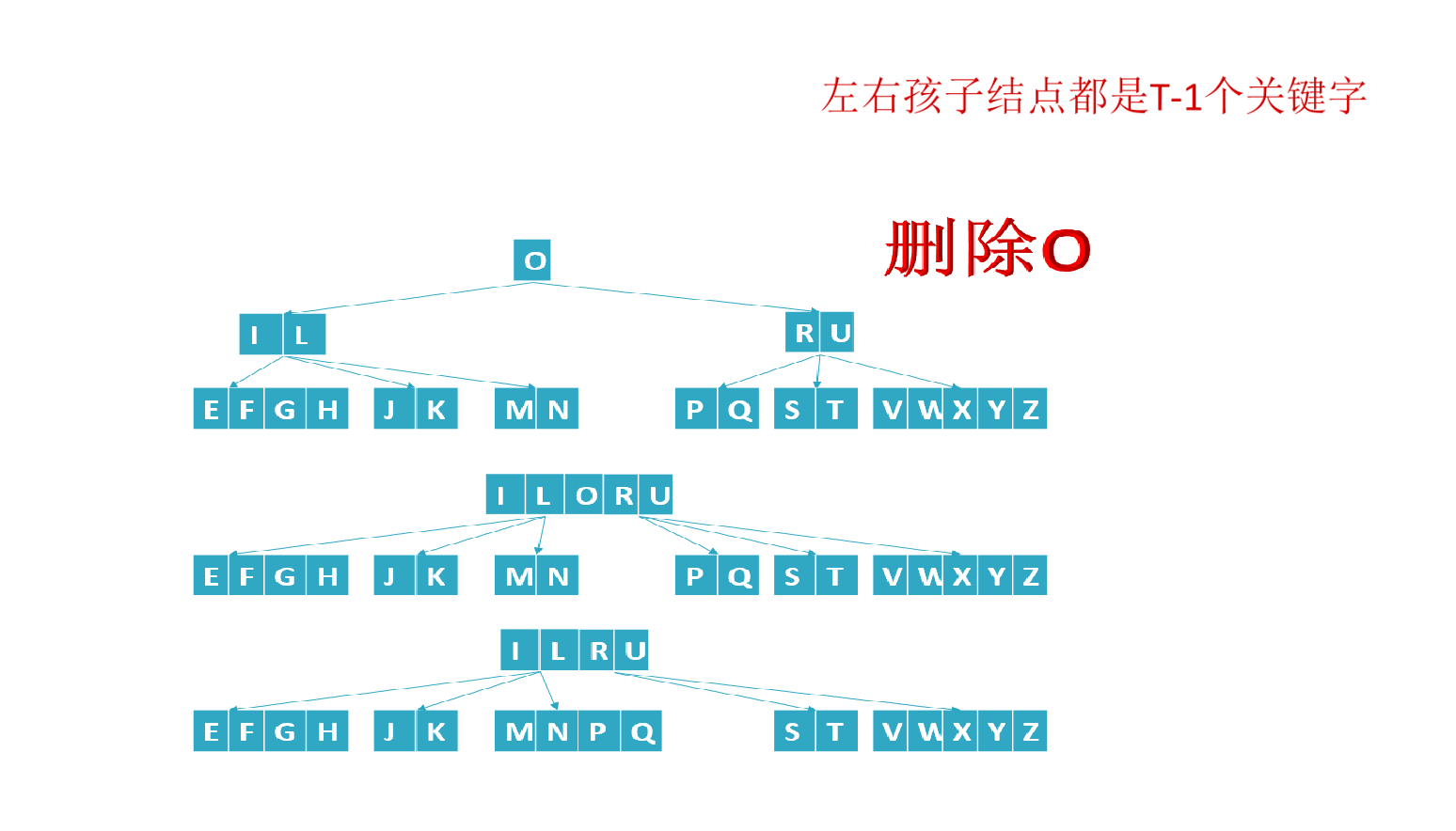
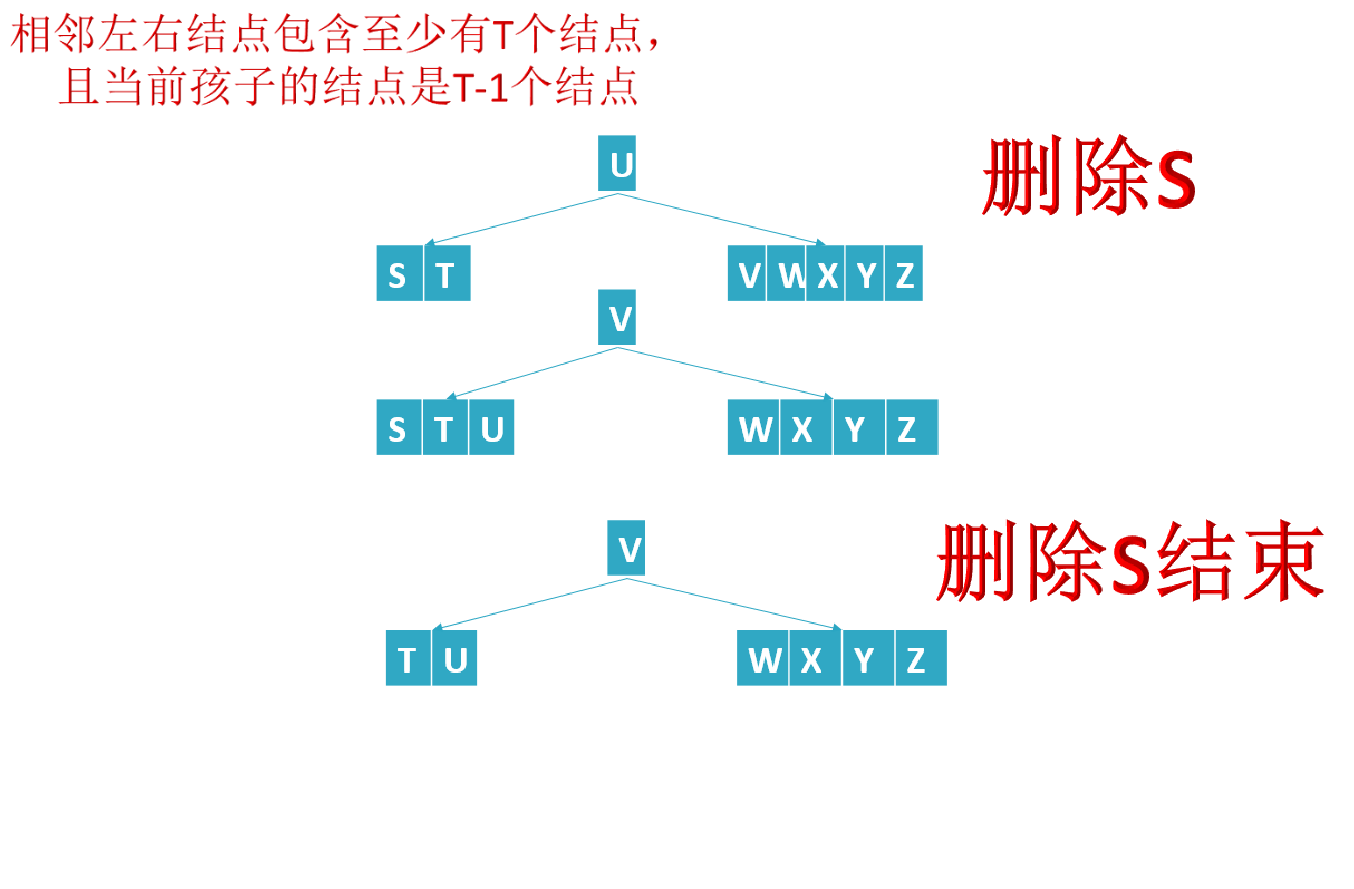
- If the number of elements (i.e. the number of key words) in a node is less than ceil(M/2)-1, You need to see whether an adjacent sibling node is plump (the number of elements in the node is greater than ceil(M/2)-1) (remember point c in the fifth feature of B tree in Section 1?: c) the number of keywords n of nodes other than the root node (including leaf nodes) must meet: (ceil(M/2)-1) < = n < = M-1. M represents the maximum number of M children, and N represents the number of key words. In the example of a B-tree in this section, the number of keywords n satisfies: 2 < = n < = 4);
- If it is plump, borrow an element from the parent node to meet the condition;
- If the number of nodes after borrowing is less than ceil(M/2)-1, the node and one of its adjacent siblings are "merged" into a node to meet the conditions.
If the number of subtrees with internal knots is at least T, then T = ceil(M/2)= 3:
Find operation
The search operation of B tree is basically the same as that of binary tree. The difference is that the node keywords are traversed sequentially. If found, it returns. If not found, it recursively searches the subtree corresponding to the range of keywords. It is relatively simple and will not be repeated.
To sum up, it is not difficult to find the operation code of B tree as follows:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#define DEGREE 3
typedef int KEY_VALUE;
typedef struct _btree_node {
KEY_VALUE *keys;
struct _btree_node **childrens;
int num;
int leaf;
} btree_node;
typedef struct _btree {
btree_node *root;
int t;//
} btree;
btree_node *btree_create_node(int t, int leaf) {
btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));
if (node == NULL) assert(0);
node->leaf = leaf;
node->keys = (KEY_VALUE*)calloc(1, (2*t-1)*sizeof(KEY_VALUE));
node->childrens = (btree_node**)calloc(1, (2*t) * sizeof(btree_node));
node->num = 0;
return node;
}
void btree_destroy_node(btree_node *node) {
assert(node);
free(node->childrens);
free(node->keys);
free(node);
}
void btree_create(btree *T, int t) {
T->t = t;
btree_node *x = btree_create_node(t, 1);
T->root = x;
}
void btree_split_child(btree *T, btree_node *x, int i) {
int t = T->t;
btree_node *y = x->childrens[i];
btree_node *z = btree_create_node(t, y->leaf);
z->num = t - 1;
int j = 0;
for (j = 0;j < t - 1;j++) {
z->keys[j] = y->keys[j+t];
}
if (y->leaf == 0) {
for (j = 0;j < t;j++) {
z->childrens[j] = y->childrens[j+t];
}
}
y->num = t - 1;
for (j = x->num;j >= i + 1;j--) {
x->childrens[j+1] = x->childrens[j];
}
x->childrens[i+1] = z;
for (j = x->num-1;j >= i;j--) {
x->keys[j+1] = x->keys[j];
}
x->keys[i] = y->keys[t-1];
x->num += 1;
}
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {
//Remove the root node and split other nodes
int i = x->num - 1;
if (x->leaf == 1) {//leaf node
while (i >= 0 && x->keys[i] > k) {
x->keys[i+1] = x->keys[i];
i--;
}
x->keys[i+1] = k;
x->num += 1;
} else {
while (i >= 0 && x->keys[i] > k) i --;
if (x->childrens[i+1]->num == (2*(T->t))-1) {
btree_split_child(T, x, i+1);
if (k > x->keys[i+1]) i++;
}
btree_insert_nonfull(T, x->childrens[i+1], k);
}
}
void btree_insert(btree *T, KEY_VALUE key) {
//int t = T->t;
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) {//Root node splitting operation
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->childrens[0] = r;
btree_split_child(T, node, 0);
int i = 0;
if (node->keys[0] < key) i++;
btree_insert_nonfull(T, node->childrens[i], key);
} else {
btree_insert_nonfull(T, r, key);
}
}
void btree_traverse(btree_node *x) {
int i = 0;
for (i = 0;i < x->num;i ++) {
if (x->leaf == 0)
btree_traverse(x->childrens[i]);
printf("%C ", x->keys[i]);
}
if (x->leaf == 0) btree_traverse(x->childrens[i]);
}
void btree_print(btree *T, btree_node *node, int layer)
{
btree_node* p = node;
int i;
if(p){
printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
for(i = 0; i < node->num; i++)
printf("%c ", p->keys[i]);
printf("\n");
layer++;
for(i = 0; i <= p->num; i++)
if(p->childrens[i])
btree_print(T, p->childrens[i], layer);
}
else printf("the tree is empty\n");
}
int btree_bin_search(btree_node *node, int low, int high, KEY_VALUE key) {
int mid;
if (low > high || low < 0 || high < 0) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (key > node->keys[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return low;
}
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
btree_node *left = node->childrens[idx];
btree_node *right = node->childrens[idx+1];
int i = 0;
/data merge
left->keys[T->t-1] = node->keys[idx];
for (i = 0;i < T->t-1;i++) {
left->keys[T->t+i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0;i < T->t;i ++) {
left->childrens[T->t+i] = right->childrens[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx+1;i < node->num;i ++) {
node->keys[i-1] = node->keys[i];
node->childrens[i] = node->childrens[i+1];
}
node->childrens[i+1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {
if (node->leaf) {
for (i = idx;i < node->num-1;i++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return;
}
else if (node->childrens[idx]->num >= T->t) {
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
}
else if (node->childrens[idx+1]->num >= T->t) {
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
}
else {
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
}
else {
btree_node *child = node->childrens[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
}
else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->keys[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num--;
}
}
else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx - 1);
child = left;
}
else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_VALUE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
int main() {//test case
btree T = {0};
btree_create(&T, 3);
srand(48);
int i = 0;
char key[52] = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";
for (i = 0;i < 52;i ++) {
//key[i] = rand() % 1000;
printf("%c ", key[i]);
btree_insert(&T, key[i]);
}
btree_print(&T, T.root, 0);
for (i = 0;i < 52;i ++) {
printf("\n---------------------------------\n");
btree_delete(&T, key[51-i]);
//btree_traverse(T.root);
btree_print(&T, T.root, 0);
}
}