C language learning notes - trigonometric function

common trigonometric functions are provided in the C language standard library in the header file math You can see the relevant definitions of functions in H.

  double __cdecl sin(double _X);
  double __cdecl cos(double _X);
  double __cdecl tan(double _X);
  double __cdecl asin(double _X);
  double __cdecl acos(double _X);
  double __cdecl atan(double _X);
  double __cdecl atan2(double _Y,double _X);

where the parameters of sin, cos and tan functions are an angle expressed in radians, and return the sine, cosine and tangent values of this angle respectively.

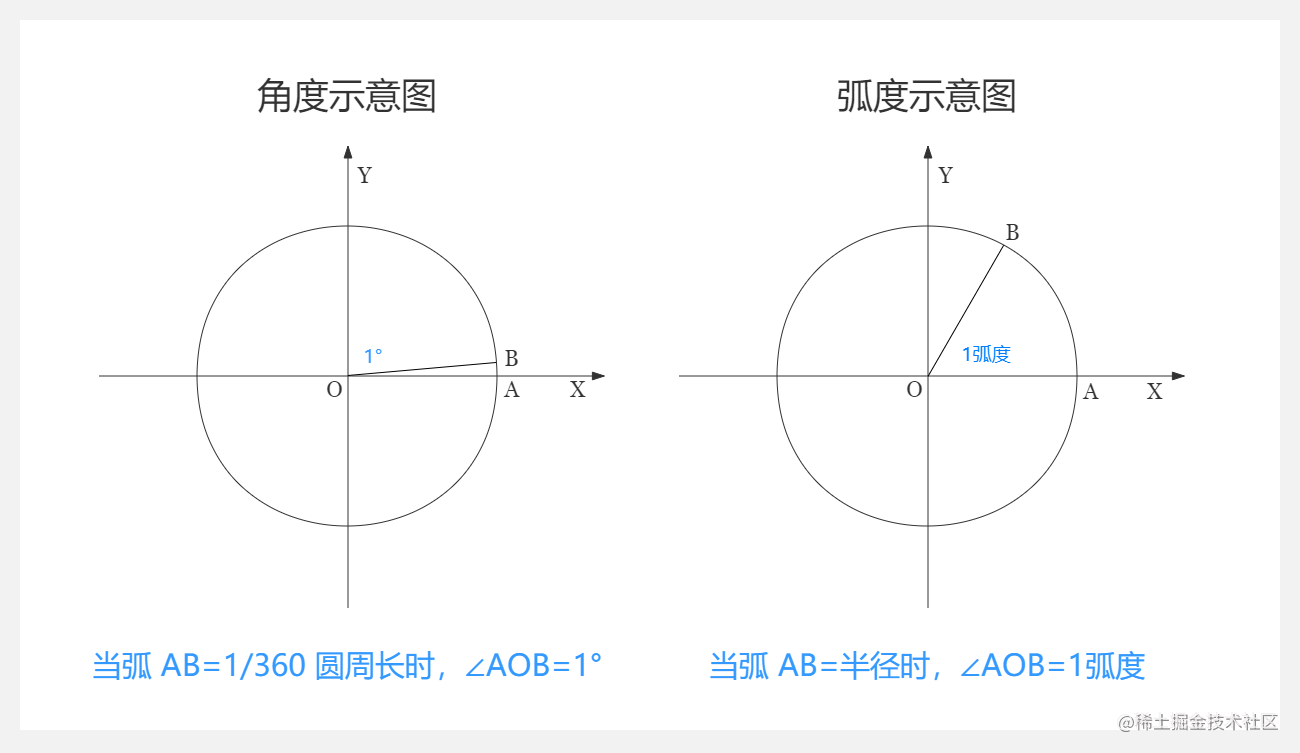
degrees and radians are units to measure the size of angles. Degrees are expressed in degrees and radians in rad.

Definition of radian

in a circle, the central angle of the arc whose arc length is equal to the radius is 1rad. In other words, two rays are emitted from the center of the circle to the circumference, forming an arc with an included angle opposite to the included angle. When the length of this arc is exactly equal to the radius of the circle, the radian of the included angle of the two rays is 1.

Definition of degree

Two rays are emitted from the center of the circle to the circumference, forming an arc with an included angle opposite to the included angle. When the arc length is exactly equal to one 360 of the circumference of the circle, the angle between the two rays is 1 degree.

It can be seen from this:

π = 8153 radians / 81950 radians

Therefore, the formula for converting degrees into radians is obtained:

radian = degree × π/180
For example:

30°＝30 × π / 180 = π / 6 radians
45°＝45 × π / 180 = π / 4 radians
60°＝60 × π / 180 = π / 3 radians
90°＝90 × π / 180 = π / 2 radians
120°＝120 × π / 180 = 2 π / 3 radians
180°＝180 × π / 180 = π radian

Conversely, how does radian turn into degree?

Because π radian = 180 °

So 1 radian = 180 ° / π (≈ 57.3 °)

Therefore, the formula for converting radians into degrees can be obtained:

Degree = radian × 180°/π

For example:

π / 2 radian = π / 2 × 180°/π =90°
4 π / 3 radian = 4 π / 3 × 180°/π =240°

The sin, cos and tan functions are defined as follows:

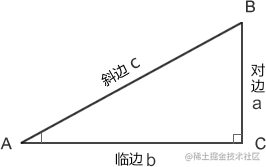
In right triangle ABC (where angle c is 90 °), the sine of angle a is the ratio of the length of its opposite side to the length of the hypotenuse of the triangle, sinA = a / c.
In right triangle ABC (where angle c is 90 °), the cosine of angle A is the ratio of its edge length to the length of the hypotenuse of the triangle, cosA = b / c.
In right triangle ABC (where angle C is 90 °), the tangent of angle a is the ratio of its opposite side length to its adjacent side length, tanA = a / b.

Here is a simple code to demonstrate the usage of these trigonometric functions.

#include <stdio.h>
#include <math.h>

#define PI 3.14159265

int main ()
{
   double x, ret, val;

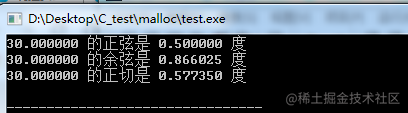
   x = 30.0;
   val = PI / 180;
   ret = sin(x*val);
   printf("%lf The sine of is %lf degree\n", x, ret);
   
   ret = cos(x*val);
   printf("%lf The cosine of is %lf degree\n", x, ret);   
   
   ret = tan(x*val);
   printf("%lf The tangent of is %lf degree\n", x, ret);
   
   return(0);
}

The output results are as follows:

The asin(), acos and atan functions return the inverse sine, inverse cosine and arctangent values of their parameters respectively. Functions just like
The sin, cos and tan functions are opposite.

sin() is the radian value x of an angle, and find the sine value y of the angle; And asin() is the sine value y of an angle and the radian value x of the angle. The value of X must be in the interval [- 1, 1]. If the value of X exceeds this interval, an error will be generated.

the test code is as follows:

#include <stdio.h>
#include <math.h>

#define PI 3.14159265

int main ()
{
   double x, ret, val;
   x = 1.0;
   val = 180.0 / PI;

   ret = asin(x) * val;
   printf("%lf The inverse sine of is %lf degree\n", x, ret);
   
   ret =acos(x) * val;
   printf("%lf The inverse cosine of is %lf degree\n", x, ret);   
   
   ret = atan(x) * val;
   printf("%lf Yes, anyway %lf degree\n", x, ret);
   
   return(0);
}

the output result is:

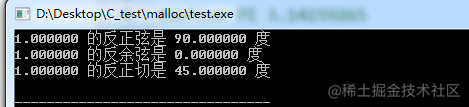
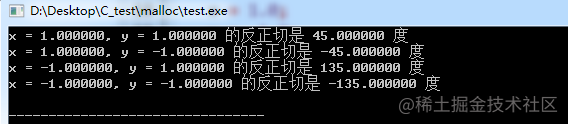
finally, there is an arctangent function atan2. atan2() is an enhanced version of atan(), which can determine the quadrant of the angle. It returns the arctangent of y/x in radians. The sign of the values of y and x determines the correct quadrant.

It has two parameters:

x – floating point value representing x-axis coordinates.
y – floating point value representing y-axis coordinates.

The radian interval is [- π, + π].
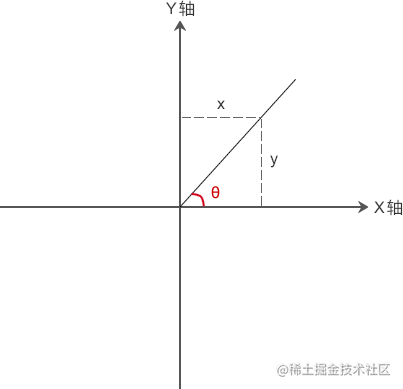
When (x, y) is in the quadrant:

When (x, y) is in the first quadrant, 0< θ < π/2
When (x, y) is in the second quadrant, π / 2< θ ≤ π
When (x, y) is in the third quadrant, - π< θ < - π/2
When (x, y) is in the fourth quadrant, - π / 2< θ < 0

When (x, y) is on the boundary of quadrant (i.e. coordinate axis):

When y is 0 and x is nonnegative, θ = 0
When y is 0 and x is negative, θ = π
When y is positive and x is 0, θ = π/2
When y is negative and x is 0, θ = - π/2

the test code is as follows:

#include <stdio.h>
#include <math.h>

#define PI 3.14159265

int main ()
{
   double x, y, ret, val;

   val = 180.0 / PI;
   
   x = 1.0;
   y = 1.0;
   ret = atan2 (y,x) * val;
   printf("x = %lf, y = %lf Arctangent of", x, y);
   printf("yes %lf degree\n", ret);
   
   x = 1.0;
   y = -1.0;
   ret = atan2 (y,x) * val;
   printf("x = %lf, y = %lf Arctangent of", x, y);
   printf("yes %lf degree\n", ret);
   
   x = -1.0;
   y = 1.0;
   ret = atan2 (y,x) * val;
   printf("x = %lf, y = %lf Arctangent of", x, y);
   printf("yes %lf degree\n", ret);
   
   x = -1.0;
   y = -1.0;
   ret = atan2 (y,x) * val;
   printf("x = %lf, y = %lf Arctangent of", x, y);
   printf("yes %lf degree\n", ret);
     
   return(0);
}

the output results are as follows:

Keywords: C function

Added by kuliksco on Thu, 17 Feb 2022 02:49:24 +0200

Programming VIP

C language learning notes - trigonometric function

Popular Keywords