I.
Recursive and callback functions.
1. Recursive Functions
A recursive function is defined as the function itself calling itself continuously within its body until the end condition is established.
The most important part of a recursive function is the end condition. If the end condition is not present or it never holds, then a dead recursion occurs, consumes a lot of resources and will eventually result in a full stack.
Recursion is mainly used for operations that repeat many times and are not recursive when the condition is known to be true.
For example: find the factorial of N!

#include <stdio.h>
int main(){
int n ;
extern jiecheng;
n = jiecheng(100);
printf("%d\n",n);
}
int jiecheng(int n){
 n= n * n-1;
return n<=0 ? n :jiechegn(n-1);
}

Without recursion, it is estimated that you can write a loop and loop 100 times n * n-1;N-That's okay, but recursion is simpler and looks more compelling.

2. Callback function
The callback function is defined as: I have this function as a parameter in another function.
Classic usage is in the kernel: one of the parameters in request_irq is the interrupt handler for irq_handle.
When the interrupt is triggered, it jumps to irq_handle for interrupt processing.
------------------
2. Classical Sorting Algorithms

1. Quick Sort qsort (Time Complexity)
The idea of the quick sorting algorithm is to find a benchmark value, which is larger than me to the right, smaller than me to the left, and then use the array on the left and right sides of the recursion to find another benchmark value, which is larger to the right and smaller to the left.

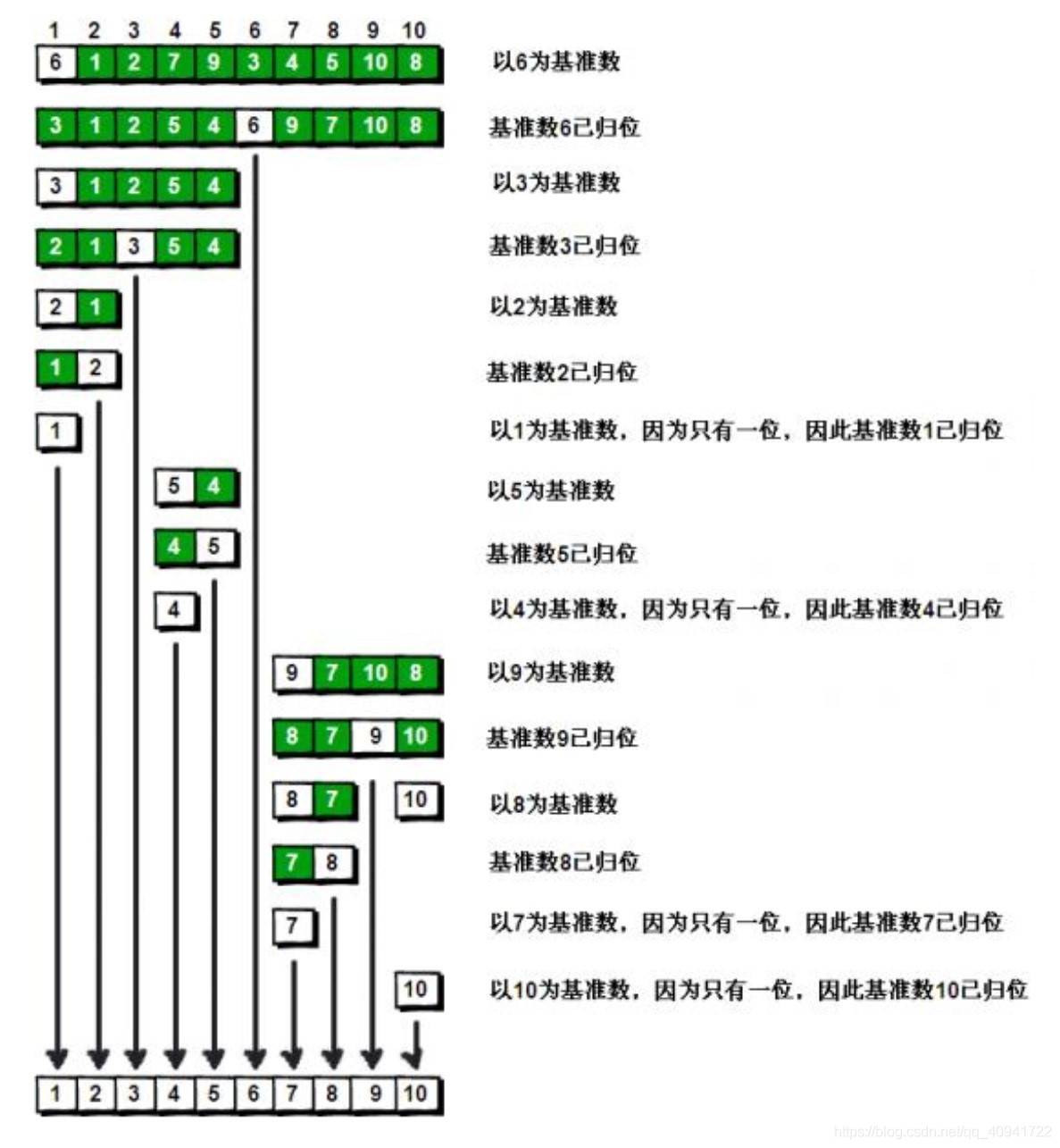
Handwritten qsort:

#include <stdio.h>
int * Qsort (int *arr,int n);
int main (){
int arr[10] = {1,2,3,5,6,,6,7,8,.3,3,2,1,,,34,5,,,6,3,,43};
Qsort(arr,10);
for(i=0；i<10;++i)
printf("%d"arr[i]);
pits("");
}
int * Qsort (int *arr,int n){
	int begin = arr[0];
	int end = arr[n];
    int tmp = arr[begin];   //Baseline value
    int i = begin; 
    int j = end; 
    while(i != j){ 			//It's still a bit clever to judge the mark that's been compared
        while(arr[j] >= tmp && j > i)  //From the back, if there is one value behind that larger than the benchmark, then the loop j --,z means that if it doesn't work, it goes back and swaps
            j--;
        while(arr[i] <= tmp && j > i) 	//Once there's a value above to swap, I'll also look for a value above the baseline to swap
            i++;
        if(j > i){			//exchange
            int t = arr[i];
            arr[i] = arr[j];
            arr[j] = t;
        }
    }
    arr[begin] = arr[i];
    arr[i] = tmp;				
    Quick_Sort(arr, begin, i-1);		
    Quick_Sort(arr, i+1, end);			//Circular comparison
}

}

2. Select Sort
Traverse through an array to find its minimum value and place it in another array. Loop n-1 times and you're done:

#include <stdio.h>
int * select(char arr[10]);
int main(){
	int arr[10] = {1,2,3,5,6,,6,7,8,.3,3,2,1,,,34,5,,,6,3,,43};
	select(char arr[10]);
	for(i=0；i<10;++i)
	printf("%d"arr[i]);
	pits("");
}
int * select(char arr[10]){
int i=0, j= 1;
int arr1[10]
while(i <=10){
	if(arr[i] < arr[j]){
		swap(arr[i],arr[j]);
		j++;
	}  //Find Minimum
	arr1[i] =arr[i];
	i++
	}
	int * p = arr1;
	return p;
}

3. Insert Sort
As opposed to sorting, for data to be inserted later, it first iterates through the sorted data to see where it fits before putting it in.

#include <stdio.h>
int * insert_sort(char arr[10]);
int main(){
	int arr[10] = {1,2,3,5,6,,6,7,8,.3,3,2,1,,,34,5,,,6,3,,43};
	select(char arr[10]);
	for(i=0；i<10;++i)
	printf("%d"arr[i]);
	pits("");
}
int * insert_sort(char arr[10]){
int i=0;
int j = 10;
int arr1[10];  //Used to store the final result
for(;i<10;i++){
int t =0;
for(;arr1[t]< arr[i];++t){
}
for(;t < i ;t++){
temp = arr1[t+1];
arr1[t+1] = arr1[t];
arr1[t+2] = temp;
}
return *p = arr1;
}

4. Heap Sorting
1. Use the data structure of the tree to compare the values of left and right children, so that the value of the node is larger than the value of the child to get a big heap.
2. Swap the top of a heap with the last element of an array.
3. Rearrange the remaining elements into a large heap.
Okay, I don't understand, I don't understand, how can I do it???

5. Bubble sorting (too simple, not to mention)

-----------------
3. Data structure
Trees,
typedf struct tree{
data_t data;
struct tree* lchild ,*rchild;
}

Tree traversal.

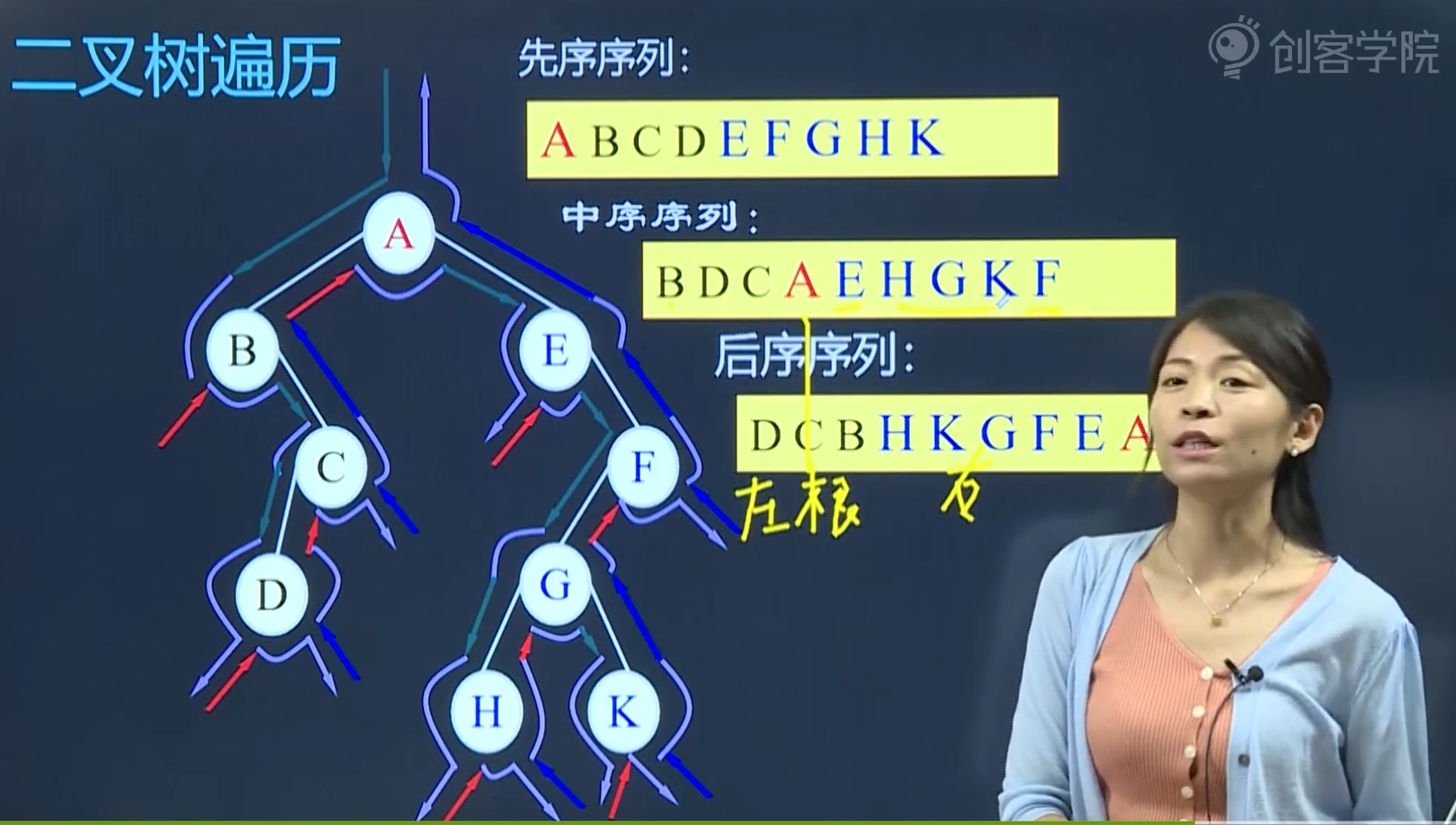
If you traverse through it, you will have no problem as long as you strictly follow the root-left, left-right, and left-right methods.
eg: Instances are ordered once.
Left and right roots, from the beginning of the node, left is B B as the root of the next node also according to the left root right is not, then the first number is B
If there is no root on the left, then C is written on the right, but C is also used as a root, and D is written on the left and C is written on the right. Follow this logic.

#include<stdio.h>
#include<stdlib.h>
#include"tree.h"

bitree * tree_create(){
	bitree *r;
	datatype ch;
	scanf("%c",&ch);
	if(ch=='#'){
		return NULL;}
	if((r=(bitree *)malloc(sizeof(bitree)))==NULL){
		return NULL;}
	r->data=ch;
	r->left=tree_create();
	r->right=tree_create();
	return r;
}

void preorder(bitree *r){
	if(r==NULL){
		return;}
	printf("%c",r->data);
	preorder(r->left);
	preorder(r->right);
	return;
}

void inorder(bitree *r){

	if(r==NULL){
		return;}
	preorder(r->left);
	printf("%c",r->data);
	preorder(r->right);
	return;
}

void postorder(bitree *r){

	if(r==NULL){
		return;}
	preorder(r->left);
	preorder(r->right);
	printf("%c",r->data);
	return;
}

--------------
lookup
Sequential lookup:
Half Search:
Hash: hash
How to construct a hash function: Map the method by taking squares and preserving divisors... You can even define the method yourself.
We use the most common reserved division.
H(key) = key%p.P Best prime
Place it in the H position of the index table. For example, if I have a prime number of 53, p is 7, then it is placed in the 7th position of the hash index table. The index table can be seen as an array.
Size of index table: Fill factor a = n/m.0.7~0.8
Conflict handling method: Chain Address method, which pulls the number of conflicts into the list that should be chained.

#include<stdio.h>
#include<stdlib.h>
#include"hash.h"
#include<string.h>


hash * hash_create(){
	hash *HT;
	if((HT=(hash *)malloc(sizeof(hash)))==NULL){
		printf("malloc hash failed\n");
		return NULL;}
	memset(HT,0,sizeof(hash));
	
	return HT;}

int hash_insert(hash *HT,datatype key){
	linklist p,q;
	if(HT==NULL){
	return -1;}
//create a new node p deposit key
	if((p=(linklist )malloc(sizeof(linknode)))==NULL){
		printf("linklist malloc falied\n");
		return -1;}
	p->key=key;
	p->vaule=key%N;
	p->next=NULL;
//insert
	q=&(HT->data[key%N]);   //q points to data[vaule}//of course not written as data[vaule]
	while(q->next&&q->next->key>p->key){
	q=q->next;
	p->next=q->next;
	q->next=p;}

	return 0;}


linklist  hash_search(hash *HT,datatype key){
	linklist p;
	if(HT==NULL){
	return NULL;}
	p=&(HT->data[key%N]);
	while(p->next&&p->next->key!=key){
	p=p->next;}//ergodic
	if(p->next=NULL){
	return NULL;}
	else {
	printf("found:\n");
	return p->next;}