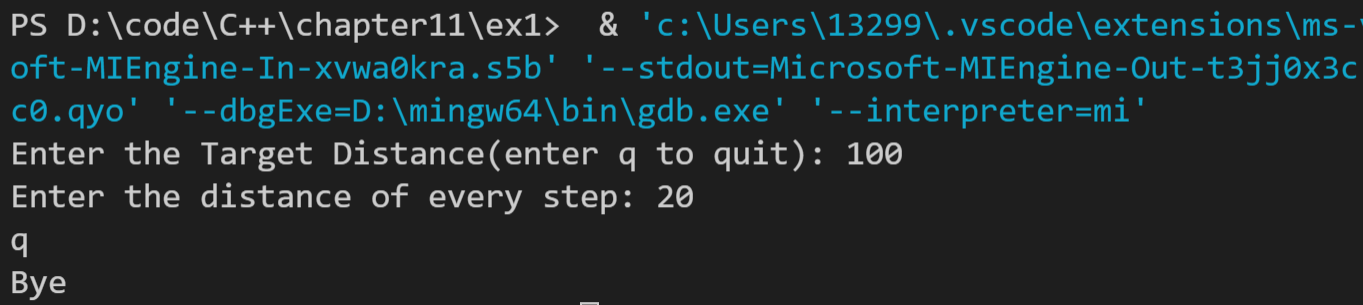
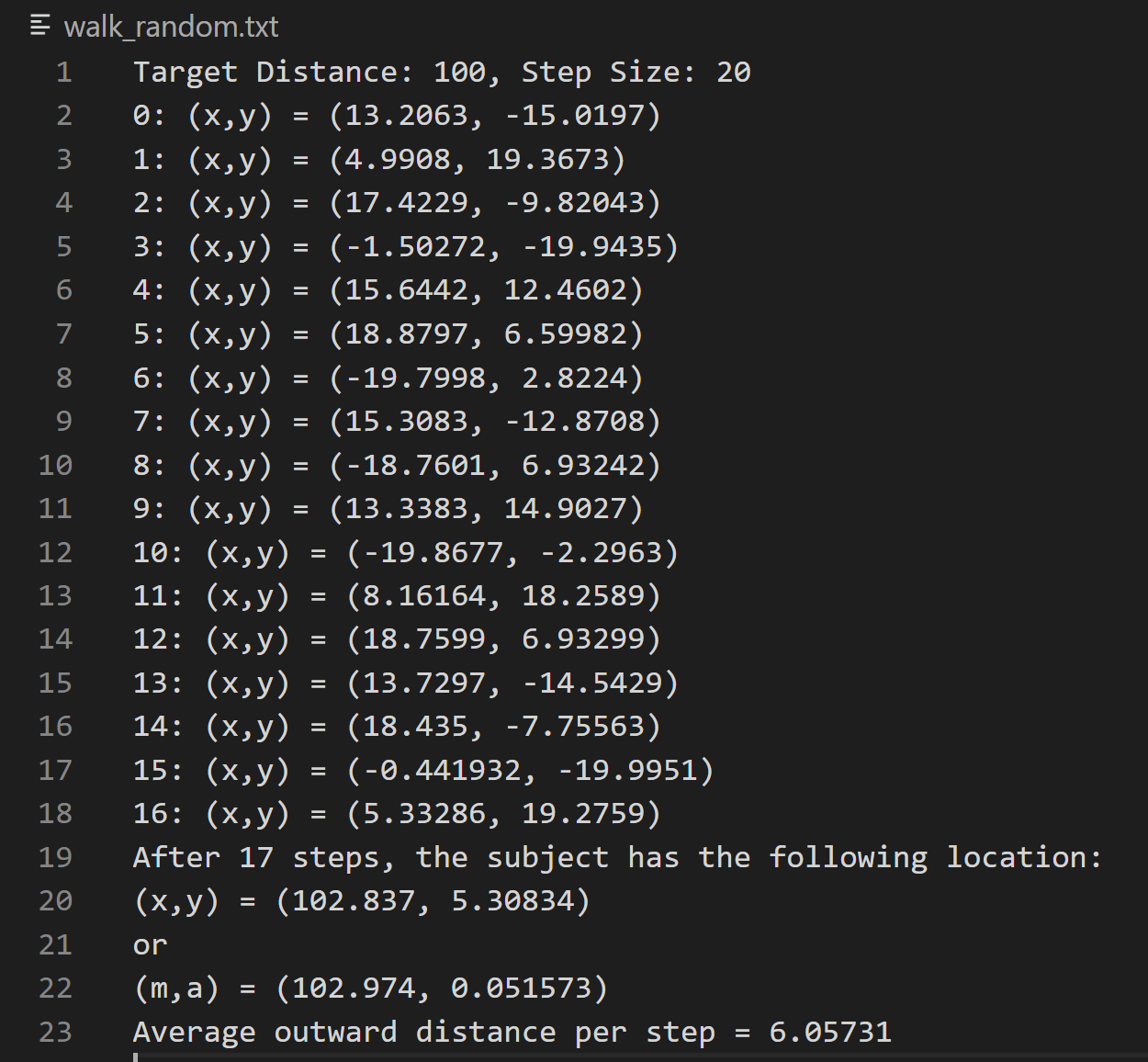
1. Modify program listing 11.5 to write a series of consecutive random walker positions to the file. Each position is marked with a step number. In addition, let the program write the initial conditions (target distance and step size) and the result summary into the file. The content of the file is similar to the following:
Target Distance: 100, Step Size: 20
0: (x,y) = (0,0)
1: (x,y) = (-11.4715, 16.383)
2: (x,y) = (-8.68807, -3.42232)
...
26: (x,y) = (42.2919, -78.2594)
27: (x,y) = (58.6794, -89.7309)
After 27 steps, the subject has the following location:
(x,y) = (58.6749, -89.7309)
or
(m,a) = (107.212, -56.8194)
This problem is relatively easy. Help the skilled program to write the file again. vector.h and vector CPP is included in this chapter. The main function program is as follows:
// ex1.cpp -- walk random problem
// compile with vector.cpp
#include <fstream>
#include <cstdlib> // rand(), srand() protypes
#include <ctime> // time() protype
#include "vector.h"
int main()
{
using namespace std;
using VECTOR::Vector;
// write in file
ofstream fout;
fout.open("walk_random.txt");
srand(time(0)); //generate a seed of random
double target;
double dstep;
unsigned long steps = 0;
Vector step;
Vector result(0.0,0.0);
cout << "Enter the Target Distance(enter q to quit): ";
while(cin >> target)
{
cout << "Enter the distance of every step: ";
while(!(cin >> dstep))
{
cin.clear();
while(cin.get() != '\n')
continue;
cout << "Bad input, please enter a double value: ";
}
fout << "Target Distance: " << target << ", Step Size: " << dstep << endl;
while(result.mag_val() < target)
{
step.reset(dstep, rand() % 360, Vector::POL);
step.rect_mode();
fout << steps << ": " << step << endl;
result = result + step;
steps++;
}
fout << "After " << steps << " steps, the subject has the following location:\n";
fout << result << endl;
fout << "or\n";
result.polar_mode();
fout << result << endl;
fout << "Average outward distance per step = " << result.mag_val() / steps << endl;
cout << "Enter next Target Distance(enter q to quit): ";
}
fout.close();
cout << "Bye\n";
return 0;
}
The operation results are as follows:
The generated files are as follows:
2. Modify the header file (program listing 11.13) and implementation file (program listing 11.14) of Vector class so that they no longer store the length and angle of vectors, but calculate them when magval() and angvel() are called.
The public interface shall remain unchanged (the public methods and their parameters remain unchanged), but the private part, including some private methods and implementations, shall be modified. Then use program listing 11.15 to test the modified version, and the result should be the same as before, because the public interface of Vector class is the same as the original.
First, modify the vector h. Delete the private members mag and ang, delete the four set functions, then modify the constructor and reset() function, modify the magval() and angvel() functions after modification, and finally modify the friend output function. The code is as follows:
// vector1.h -- Vector class with <<, mode state
// store Vector use x and y
#ifndef VECTOR1_H_
#define VECTOR1_H_
#include <iostream>
namespace VECTOR
{
class Vector
{
public:
enum Mode{RECT, POL};
// RECT for rectangular, POL for Polar modes
private:
double x;
double y;
Mode mode;
// private methods for setting values;
public:
Vector();
Vector(double n1, double n2, Mode form = RECT);
void reset(double n1, double n2, Mode form = RECT);
~Vector();
double xval() const {return x;}
double yval() const {return y;}
double magval() const;
double angval() const;
void polar_mode(); // set mode to POL
void rect_mode(); // set mode to RECT
// oprator overloading
Vector operator+(const Vector & b) const;
Vector operator-(const Vector & b) const;
Vector operator-()const;
Vector operator*(double n) const;
// friends
friend Vector operator*(double n, const Vector & a);
friend std::ostream &
operator<<(std::ostream & os, const Vector & v);
};
} // end namespace VECTOR
#endif
// vector1.cpp -- methods for the Vector class
#include <cmath>
#include "vector1.h"
using std::sqrt;
using std::sin;
using std::cos;
using std::atan;
using std::atan2;
using std::cout;
namespace VECTOR
{
const double Rad_to_deg = 45.0/atan(1.0);
// should be about 57.2957795130823
Vector::Vector()
{
x = y = 0;
mode = RECT;
}
Vector::Vector(double n1, double n2, Mode form )
{
mode = form;
if(mode == RECT)
{
x = n1;
y = n2;
}
else if(mode == POL)
{
double ang = n2 / Rad_to_deg;
x = n1 * cos(ang);
y = n1 * sin(ang);
}
else
{
cout << "Incorrect 3rd argument to Vector() --";
cout << "vector set to 0\n";
x = y = 0;
mode = RECT;
}
}
// reset vector from rectangular cooridinates if form is
// RECT (the default) or else from polar coordinates if
// form is POL
void Vector::reset(double n1, double n2, Mode form)
{
mode = form;
if(mode == RECT)
{
x = n1;
y = n2;
}
else if(mode == POL)
{
double ang = n2 / Rad_to_deg;
x = n1 * cos(ang);
y = n1 * sin(ang);
}
else
{
cout << "Incorrect 3rd argument to Vector() --";
cout << "vector set to 0\n";
x = y = 0;
mode = RECT;
}
}
Vector::~Vector() // destructor
{
}
double Vector::magval() const
{
return sqrt(x * x + y * y);
}
double Vector::angval() const
{
if(x == 0.0 && y == 0.0)
return 0;
else
return atan2(y,x);
}
void Vector::polar_mode() // set to polar mode
{
mode = POL;
}
void Vector::rect_mode() // set to rect mode
{
mode = RECT;
}
// operator overloading
// add two Vectors
Vector Vector::operator+(const Vector & b) const
{
return Vector(x + b.x, y + b.y);
}
// subtract Vector b from a
Vector Vector::operator-(const Vector & b) const
{
return Vector(x - b.x, y - b.y);
}
// reverse sign of Vector
Vector Vector::operator-() const
{
return Vector(-x, -y);
}
// multiply vector by n
Vector Vector::operator*(double n) const
{
return Vector(n * x, n * y);
}
// friend methods
// mutiply n by Vector a
Vector operator*(double n, const Vector & a)
{
return a * n;
}
std::ostream & operator<<(std::ostream & os, const Vector & v)
{
if(v.mode == Vector::RECT)
os << "(x,y) = (" << v.x << ", " << v.y << ")";
else if(v.mode == Vector::POL)
{
os << "(m,a) = (" << v.magval() << ", " << v.angval() * Rad_to_deg << ")";
}
else
os << "Vector object mode is invalid";
return os;
}
} // end namespace VECTOR
The operation results are as follows:

3. Modify program listing 11.15 to report the highest, lowest and average steps in N tests (where N is the integer entered by the user), rather than reporting the results each time.
Firstly, define an array to store the results of each experiment, and then write three functions to calculate the average, minimum and maximum values of the array. Use a loop to perform the experiment of inputting times. Note that the result needs to be initialized. The code is as follows:
// ex3.cpp -- rand walk problem
// compile with the vect.cpp file
#include <cstdlib> // rand(), srand() protypes
#include <ctime> // time() protype
#include "vector1.h"
unsigned long average(unsigned long arr[],int n);
unsigned long findmax(unsigned long arr[],int n);
unsigned long findmin(unsigned long arr[],int n);
int main()
{
using namespace std;
using VECTOR::Vector;
srand(time(0)); // seed random-number generator
double direction;
Vector step;
Vector result(0.0, 0.0);
double target;
double dstep;
int times;
cout << "Enter target distance: ";
cin >> target;
cout << "Enter step length: ";
cin >> dstep;
cout << "Enter the times you want to test: ";
cin >> times;
unsigned long steps[times];
for(int i = 0; i < times; i++)
{
// initialize and reset result to 0
steps[i] = 0;
result.reset(0.0, 0.0); // is necessary
while(result.magval() < target)
{
direction = rand() % 360;
step.reset(dstep, direction, Vector::POL);
result = result + step;
steps[i]++;
}
}
unsigned long steps_max = findmax(steps, times);
unsigned long steps_min = findmin(steps, times);
unsigned long steps_ave = average(steps, times);
cout << "After " << times << " times test:\n";
cout << "Maximum steps is " << steps_max << endl;
cout << "Minimun steps is " << steps_min << endl;
cout << "Average steps is " << steps_ave << endl;
cout << "Bye!\n";
cin.clear();
while(cin.get() != '\n')
continue;
return 0;
}
unsigned long average(unsigned long arr[],int n)
{
unsigned long long sum = 0;
for(int i = 0; i < n; i++)
{
sum += arr[i];
}
return sum / n;
}
unsigned long findmax(unsigned long arr[],int n)
{
unsigned long max = 0;
for(int i = 0; i < n; i++)
max = max < arr[i] ? arr[i] : max;
return max;
}
unsigned long findmin(unsigned long arr[],int n)
{
unsigned long min = arr[0];
for(int i = 0; i < n; i++)
min = min < arr[i] ? min : arr[i];
return min;
}
The operation results are as follows:
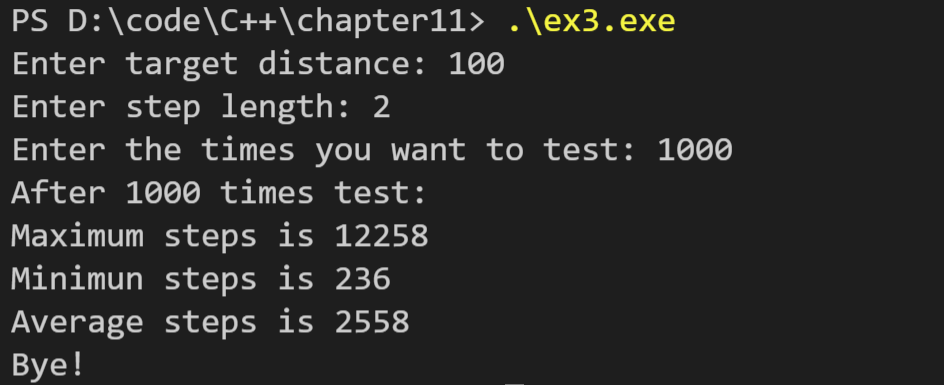
You can see that the result is close to 100 / 2 square, so it is correct.
4. Rewrite the last Time class example (program listing 11.10, program listing 11.11 and program listing 11.12) and use friend functions to implement all overloaded operators.
This problem is not difficult. It should be noted that since the function is outside the class, the function cannot be declared as const. Procedures 11.10 and 11.11 need to be modified, and class use procedures do not need to be modified. The procedures are as follows:
// mytime.h -- Time class operator * and << overloading
#ifndef MYTIME_H_
#define MYTIME_H_
#include <iostream>
class Time
{
private:
int hours;
int minutes;
public:
Time();
Time(int h, int m = 0);
void AddMin(int m);
void AddHr(int h);
void Reset(int h = 0, int m = 0);
// friend
friend Time operator+(const Time & t1, const Time & t2);
friend Time operator-(const Time & t1, const Time & t2);
friend Time operator*(const Time & t, double n);
friend Time operator*(double n, const Time & t) {return t * n;}
friend std::ostream & operator<<(std::ostream & os,const Time & t);
};
#endif
// mytime.cpp -- implementing Time methods
#include <iostream>
#include "mytime.h"
Time::Time()
{
hours = minutes = 0;
}
Time::Time(int h, int m)
{
hours = h;
minutes = m;
}
void Time::AddMin(int m)
{
minutes += m;
if(minutes > 60)
{
hours += minutes / 60;
minutes %= 60;
}
}
void Time::AddHr(int h)
{
hours += h;
}
Time operator+(const Time & t1, const Time & t2)
{
Time sum;
sum.hours = t1.hours;
sum.minutes = t2.minutes;
sum.AddMin(t2.minutes);
sum.AddHr(t2.hours);
return sum;
}
Time operator-(const Time & t1, const Time & t2)
{
Time diff;
diff.minutes = t1.minutes - t2.minutes;
diff.hours = t1.hours - t2.hours;
if(diff.minutes < 0)
{
diff.minutes = 60 - diff.minutes;
diff.hours -= 1;
}
return diff;
}
Time operator*(const Time & t, double n)
{
Time result;
long totalminutes = (t.hours * 60 + t.minutes) * n;
result.minutes = totalminutes % 60;
result.hours = totalminutes / 60;
return result;
}
std::ostream & operator<<(std::ostream & os,const Time & t)
{
os << t.hours << " hours, " << t.minutes << " minutes";
return os; // is necessary
}
// usetime3_11_12.cpp -- using the third draft of the Time class
// compile usetime3.cpp and mytime0.cpp together
#include "mytime.h"
int main()
{
using std::cout;
using std::cin;
using std::endl;
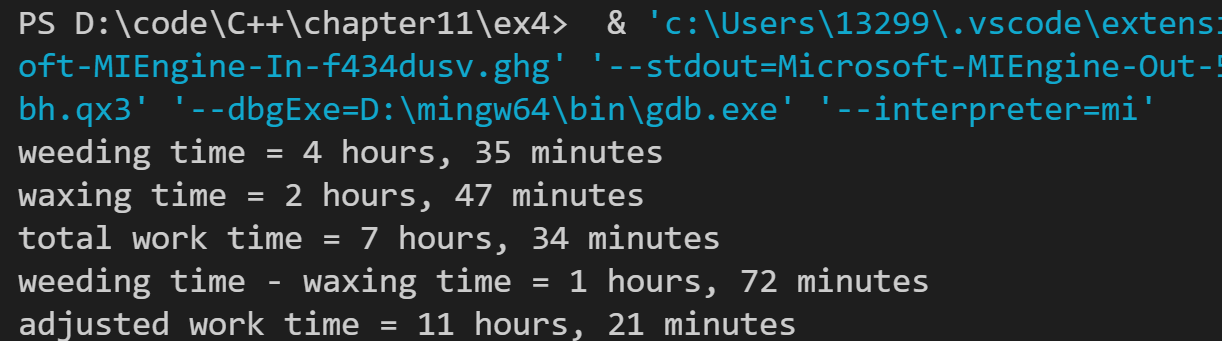
Time weeding(4,35);
Time waxing(2,47);
Time total,diff,adjusted;
cout << "weeding time = " << weeding << endl;
cout << "waxing time = " << waxing << endl;
total = weeding + waxing;
cout << "total work time = " << total << endl;
diff = weeding - waxing;
cout << "weeding time - waxing time = " << diff << endl;
adjusted = 1.5 * total;
cout << "adjusted work time = " << adjusted << endl;
return 0;
}
The operation results are as follows:
5. Rewrite Stonewt class (program listing 11.16 and program listing 11.17) to have a status member, which controls whether the object should be converted to quartz format, integer point format or floating point point point format. Overload the < < operator and use it to replace show_stn() and show_lbs() method. Overload the addition, subtraction, and multiplication operators so that you can add, subtract, and multiply Stonewt values. Write a small program that uses all classes to test this class.
There are two ways to modify this question. One is that when storing, the data in three formats are stored and distinguished by mode. The data in that format can be called by object members; The other way is to select only one format for storage. When other formats are needed, use the calculation function to calculate the return value. The second format is adopted by the author. During writing, the constructor encountered problems, and the default parameters were not used, resulting in incorrect output format. Add mode = form to solve the problem. The sample code is as follows:
// stonewt.h -- definetion for the Stonewt class
#ifndef STONEWT_H_
#define STONEWT_H_
#include <iostream>
using std::ostream;
class Stonewt
{
public:
enum MODE {STONE, POUNDS, INT_POUNDS};
private:
enum{Lbs_per_stn = 14}; // pounds per stone
double pounds; // entire weight in pounds
MODE mode;
public:
Stonewt(double lbs, MODE form = POUNDS);
Stonewt(int stn, double lbs, MODE form = STONE);
Stonewt(int lbs, MODE form = INT_POUNDS);
Stonewt();
~Stonewt();
//get value
int stone_val() const;
double pds_left_val() const;
double pounds_val() const;
int int_pounds_val() const;
// set mode
void pounds_mode();
void int_pounds_mode();
void stone_mode();
// operator + - *
Stonewt operator+(const Stonewt & st) const;
Stonewt operator-(const Stonewt & st) const;
Stonewt operator*(double n) const;
//friend
// operator*
friend Stonewt operator*(double n, const Stonewt & st);
//operator<<
friend ostream & operator<<(ostream & os, const Stonewt & st);
};
#endif
// stonewt.cpp -- Stonewt methods
#include "stonewt.h"
// construct Stonewt object from double value
Stonewt::Stonewt(double lbs, MODE form)
{
mode = form; // is necessary
pounds = lbs;
}
// construct Stonewt object from stone, double values
Stonewt::Stonewt(int stn, double lbs, MODE form)
{
mode = form;
pounds = stn * Lbs_per_stn + lbs;
}
// construct Stonewt object form int pounds vlaue
Stonewt::Stonewt(int lbs, MODE form)
{
mode = form;
pounds = double(lbs);
}
// default constructor, wt = 0
Stonewt::Stonewt()
{
pounds = 0;
}
Stonewt::~Stonewt() // destructor
{
}
// get value
int Stonewt::stone_val() const
{
return int(pounds) / Lbs_per_stn;
}
double Stonewt::pds_left_val() const
{
return int(pounds) % Lbs_per_stn + pounds -int(pounds);
}
double Stonewt::pounds_val() const
{
return pounds;
}
int Stonewt::int_pounds_val() const
{
return int(pounds);
}
// set mode
void Stonewt::pounds_mode()
{
mode = POUNDS;
}
void Stonewt::int_pounds_mode()
{
mode = INT_POUNDS;
}
void Stonewt::stone_mode()
{
mode = STONE;
}
// operator + - *
Stonewt Stonewt::operator+(const Stonewt & st) const
{
return Stonewt(pounds + st.pounds);
}
Stonewt Stonewt::operator-(const Stonewt & st) const
{
return Stonewt(pounds - st.pounds);
}
Stonewt Stonewt::operator*(double n) const
{
return Stonewt(n * pounds);
}
// friend
Stonewt operator*(double n, const Stonewt & st)
{
return st * n;
}
ostream & operator<<(ostream & os, const Stonewt & st)
{
Stonewt::MODE mode;
mode = st.mode;
switch (mode)
{
case Stonewt::POUNDS:
os << "Double pounds: " << st.pounds << " pounds";
break;
case Stonewt::STONE:
os << "Stone: " <<st.stone_val() << " stone, " << st.pds_left_val() << " pounds";
break;
case Stonewt::INT_POUNDS:
os << "Int pounds: " << st.int_pounds_val() << " pounds";
break;
default:
os << "Stonewt object mode is invalid";
break;
}
}
// ex5_main.cpp -- test the Stonewt class
// compile with stonewt.cpp
#include "stonewt.h"
int main()
{
using std::cin;
using std::cout;
using std::endl;
double pounds;
int number; // the number of egg
Stonewt egg;
Stonewt weight;
egg = Stonewt(15.0);
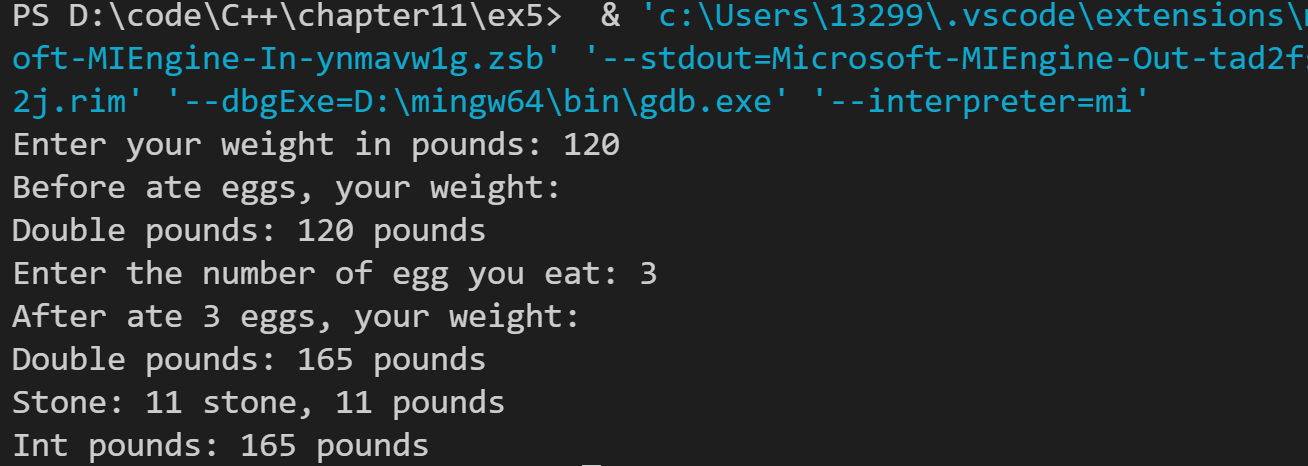
cout << "Enter your weight in pounds: ";
cin >> pounds;
weight = Stonewt(pounds);
cout << "Before ate eggs, your weight:\n";
cout << weight << endl;
cout << "Enter the number of egg you eat: ";
cin >> number;
cout << "After ate " << number << " eggs, your weight:\n";
weight = weight + number * egg;
cout << weight << endl;
weight.stone_mode();
cout << weight << endl;
weight.int_pounds_mode();
cout << weight << endl;
return 0;
}
The operation results are as follows:
6. Rewrite Stonewt class (program listings 11.16 and 11.17) and overload all 6 relational operators. Operator compares the bounds members and returns a bool value. Write a program that declares an array containing six Stonewt objects, initializes the first three objects in the array declaration, and then uses a loop to read the values used to set the remaining three array elements. Then report the smallest element, the largest element, and the number of elements greater than or equal to 11 stones (the easiest way is to create a Stonewt object, initialize it to 11 stones, and then compare it with other objects)
The knowledge of overloaded operator functions examined in this question can be overloaded by friend functions or member functions. The author adopts the method of friend function overloading, and the code is as follows:
// stonewt.h -- definetion for the Stonewt class
#ifndef STONEWT_H_
#define STONEWT_H_
#include <iostream>
using std::ostream;
class Stonewt
{
public:
enum MODE {STONE, POUNDS, INT_POUNDS};
private:
enum{Lbs_per_stn = 14}; // pounds per stone
double pounds; // entire weight in pounds
MODE mode;
public:
Stonewt(double lbs, MODE form = POUNDS);
Stonewt(int stn, double lbs, MODE form = STONE);
Stonewt(int lbs, MODE form = INT_POUNDS);
Stonewt();
~Stonewt();
//get value
int stone_val() const;
double pds_left_val() const;
double pounds_val() const;
int int_pounds_val() const;
// set mode
void pounds_mode();
void int_pounds_mode();
void stone_mode();
// operator + - *
Stonewt operator+(const Stonewt & st) const;
Stonewt operator-(const Stonewt & st) const;
Stonewt operator*(double n) const;
//friend
// operator*
friend Stonewt operator*(double n, const Stonewt & st);
// oprator == != < > <= >=
friend bool operator==(const Stonewt & st1, const Stonewt & st2);
friend bool operator!=(const Stonewt & st1, const Stonewt & st2);
friend bool operator>(const Stonewt & st1, const Stonewt & st2);
friend bool operator<(const Stonewt & st1, const Stonewt & st2);
friend bool operator<=(const Stonewt & st1, const Stonewt & st2);
friend bool operator>=(const Stonewt & st1, const Stonewt & st2);
//operator<<
friend ostream & operator<<(ostream & os, const Stonewt & st);
};
#endif
// stonewt.cpp -- Stonewt methods
#include "stonewt.h"
// construct Stonewt object from double value
Stonewt::Stonewt(double lbs, MODE form)
{
mode = form; // is necessary
pounds = lbs;
}
// construct Stonewt object from stone, double values
Stonewt::Stonewt(int stn, double lbs, MODE form)
{
mode = form;
pounds = stn * Lbs_per_stn + lbs;
}
// construct Stonewt object form int pounds vlaue
Stonewt::Stonewt(int lbs, MODE form)
{
mode = form;
pounds = double(lbs);
}
// default constructor, wt = 0
Stonewt::Stonewt()
{
pounds = 0;
}
Stonewt::~Stonewt() // destructor
{
}
// get value
int Stonewt::stone_val() const
{
return int(pounds) / Lbs_per_stn;
}
double Stonewt::pds_left_val() const
{
return int(pounds) % Lbs_per_stn + pounds -int(pounds);
}
double Stonewt::pounds_val() const
{
return pounds;
}
int Stonewt::int_pounds_val() const
{
return int(pounds);
}
// set mode
void Stonewt::pounds_mode()
{
mode = POUNDS;
}
void Stonewt::int_pounds_mode()
{
mode = INT_POUNDS;
}
void Stonewt::stone_mode()
{
mode = STONE;
}
// operator + - *
Stonewt Stonewt::operator+(const Stonewt & st) const
{
return Stonewt(pounds + st.pounds);
}
Stonewt Stonewt::operator-(const Stonewt & st) const
{
return Stonewt(pounds - st.pounds);
}
Stonewt Stonewt::operator*(double n) const
{
return Stonewt(n * pounds);
}
// friend
Stonewt operator*(double n, const Stonewt & st)
{
return st * n;
}
bool operator==(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds == st2.pounds ? true : false;
}
bool operator!=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds != st2.pounds ? true : false;
}
bool operator>(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds > st2.pounds ? true : false;
}
bool operator<(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds < st2.pounds ? true : false;
}
bool operator>=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds >= st2.pounds ? true : false;
}
bool operator<=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds <= st2.pounds ? true : false;
}
ostream & operator<<(ostream & os, const Stonewt & st)
{
Stonewt::MODE mode;
mode = st.mode;
switch (mode)
{
case Stonewt::POUNDS:
os << "Double pounds: " << st.pounds << " pounds";
break;
case Stonewt::STONE:
os << "Stone: " <<st.stone_val() << " stone, " << st.pds_left_val() << " pounds";
break;
case Stonewt::INT_POUNDS:
os << "Int pounds: " << st.int_pounds_val() << " pounds";
break;
default:
os << "Stonewt object mode is invalid";
break;
}
}
#include "stonewt.h"
int main()
{
const int Arsize = 6;
using std::cin;
using std::cout;
using std::endl;
double lbs;
Stonewt max;
Stonewt min;
int count = 0;
Stonewt starr[Arsize] = {
100,200,300
};
for(int i = 3; i < Arsize; i++)
{
cout << "Enter the weight in pounds: ";
cin >> lbs;
starr[i] = Stonewt(lbs);
}
cout << "Stonewt array list:\n";
for(int i = 0; i < Arsize; i++)
cout << starr[i] << endl;
cout << endl;
max = starr[0];
for(int i = 0; i < Arsize; i++)
{
max = max > starr[i] ? max : starr[i];
}
cout << "The maximum Stonewt object:\n" << max << endl;
min = starr[0];
for(int i = 0; i < Arsize; i++)
{
min = min < starr[i] ? min : starr[i];
}
cout << "The minimum Stonewt object:\n" << min << endl;
Stonewt st11 = Stonewt(11,0.0);
for(int i = 0; i < Arsize; i++)
{
if(starr[i] >= st11)
count++;
}
cout << "The Stonewt array >= 11 stone number: " << count << endl;
return 0;
}
The operation results are as follows:

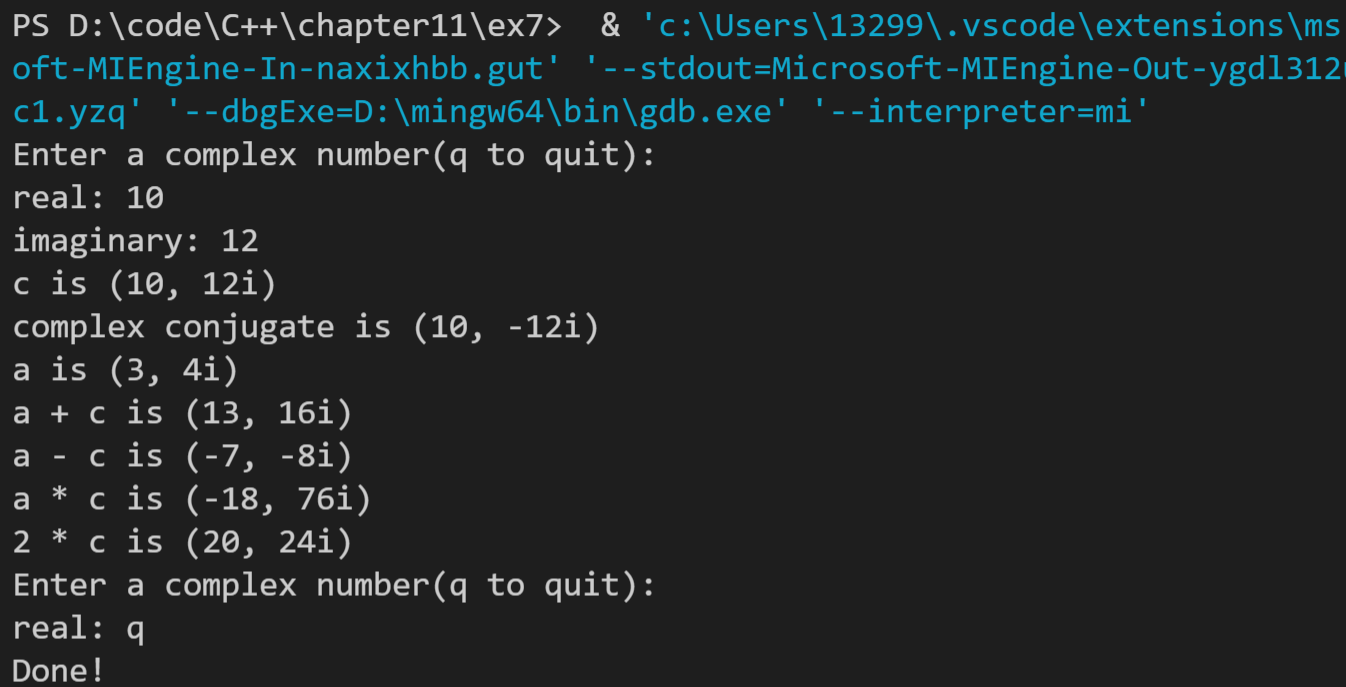
7. The plural number consists of two parts: the real part and the imaginary part. One way to write the plural is: (3.0, 4.0), where 3.0 is the real part and 4.0 is the imaginary part. Assuming a = (A, Bi) and c = (C,Di), the following are some complex calculations.
- Addition: a + c = (A + C, (B + D)i)
- Subtraction: a - c = (A - C, (B - D)i)
- Multiplication: a * c = (AC-BD,(AD+BC)i)
- Multiplication:: x c = (xC,x*Di), where x is a real number
- Conjugate: ~ a = (A,-Bi)
Please define a plural class so that the following program can use it to get the correct results.
#include <iostream>
using namespace std;
#include "complex0.h" // to avoid confusion with complex.h
int main()
{
complex a(3.0, 4.0);
complex c;
cout << "Enter a complex number(q to quit):\n";
while(cin >> c)
{
cout << "c is " << c << '\n';
cout << "complex conjugate is " << ~c << '\n';
cout << "a is " << a << '\n';
cout << "a + c is " << a + c << '\n';
cout << "a - c is " << a - c << '\n';
cout << "a * c is " << a * c << '\n';
cout << "2 * c is " << 2 * c << '\n';
cout << "Enter a complex number(q to quit):\n"
}
cout << "Done!\n";
return 0;
}
Note that the operators < < and > > must be overloaded. Standard C + + uses the header file complex, which provides more extensive plural support than this example, so the custom header file should be named complex0 h. To avoid conflicts, const should be used whenever possible.
The following is the operation of the program.
Enter a complex number(q to quit): real: 10 imaginary: 12 c is (10, 12i) complex conjugate is (10, -12i)a is (3, 4i)a + c is (13, 16i) a - c is (-7, -8i) a * c is (-18, 76i) 2 * c is (20, 24i) Enter a complex number(q to quit): real: q Done!
Note that after overloading, CIN > > C prompts the user for real and imaginary parts.
This problem is not difficult to implement. For addition, subtraction and multiplication, the member function operator overload is used. For output, it has been output before, so there is no big problem. For input, when overloading the function definition, you forget to input and cannot use const reference. Therefore, an error is prompted at the beginning, which is modified and improved later. Input q leaves, and it is not processed at the beginning, Therefore, imagear will be output: it will be solved later with if statement.
The code is as follows:
// complex0.h -- defination of complex class
#ifndef COMPLEX0_H_
#define COMPLEX0_H_
#include <iostream>
using std::ostream;
using std::istream;
class complex
{
private:
double real;
double imaginary;
public:
complex(double i, double j);
complex();
~complex();
// overloading operator + - * and ~
complex operator+(const complex & c) const;
complex operator-(const complex & c) const;
complex operator*(const complex & c) const;
complex operator~() const;
// friend
friend complex operator*(double n, const complex & c);
friend istream & operator>>(istream & os, complex & c);
friend ostream & operator<<(ostream & os, const complex & c);
};
#endif
// complex0.cpp -- methods for complex class
#include "complex0.h"
// constructor
complex::complex(double i, double j)
{
real = i;
imaginary = j;
}
complex::complex() // default
{
real = imaginary = 0.0;
}
// deconstructor
complex::~complex()
{
}
// overloading operator
complex complex::operator+(const complex & c) const
{
return complex(real + c.real, imaginary + c.imaginary);
}
complex complex::operator-(const complex & c) const
{
return complex(real - c.real, imaginary - c.imaginary);
}
complex complex::operator*(const complex & c) const
{
return complex(real * c.real - imaginary * c.imaginary, real * c.imaginary + imaginary * c.real);
}
complex complex::operator~() const
{
return complex(real, -imaginary);
}
// friend
complex operator*(double n, const complex & c)
{
return complex(n * c.real, n * c.imaginary);
}
std::istream & operator>>(std::istream & is, complex & c)
{
std::cout << "real: ";
if(is >> c.real)
{
std::cout << "imaginary: ";
is >> c.imaginary;
}
return is;
}
std::ostream & operator<<(std::ostream & os, const complex & c)
{
os << "(" << c.real << ", " << c.imaginary << "i)";
return os;
}
The operation results are as follows: