C + + problem solving difference matrix

Title Description

Enter an integer matrix with nn rows and mm columns, and then enter qq operations. Each operation contains five integers $x_1,y_1,x_2,y_2,c $, where $(x_1,y_1) and (x_2,y_2) $represent the upper left and lower right coordinates of a sub matrix.

Each operation adds $c $to the value of each element in the selected sub matrix.

Please output the matrix after all operations.

Input format

The first line contains the integer $n,m,q $.

The next $n $line contains $m $integers, representing the integer matrix.

The next $q $line contains $5 $integers $x_1,y_1,x_2,y_2,c $, indicates an operation.

Output format

There are $n $rows in total, and $m $integers in each row represent the final matrix after all operations are completed.

Data range

$$
1≤n,m≤1000\
1≤q≤100000\
1≤x_1≤x_2≤n\
1≤y_1≤y_2≤m\
−1000≤c≤1000\
− 1000 ≤ value of elements in the matrix ≤ 1000\
$$

Input example:

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

Output example:

2 3 4 1
4 3 4 1
2 2 2 2

thought

Difference is the inverse operation of prefix sum. Through difference, we can realize O (1) and add and subtract the specified interval of the matrix

Differential array:

First, give an original matrix A: a [1] [q], a [1] [2], a [1] [3],,,,, a [n] [n];

Then we construct a matrix b: b [1] [1], b [1] [2], b [1] [3],,,,, b [n] [n];

Make a [i] [i] = B [1] [1] + B [1] [2] + B [1] [3] +,,,,, + B [i] [i]

In other words, a matrix is the prefix and matrix of b matrix. Conversely, we call b matrix the difference matrix of a matrix. In other words, each a[i][i] is a sum of matrices from the beginning in the b matrix.

How to construct difference matrix

We assume that the original matrix a is all 0, and the process of assigning the initial value to the original matrix a is regarded as adding and subtracting the original matrix a with the unit of 1

example

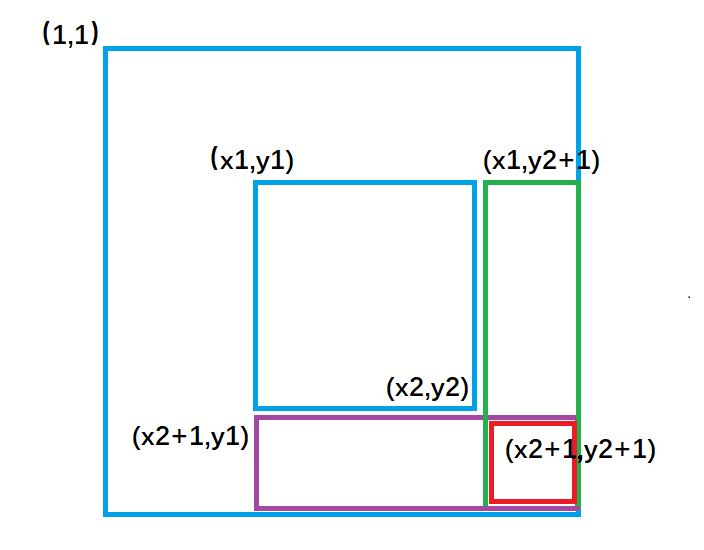
If I want to add [l,r] of matrix a, I will perform the following operations on difference matrix b

	b[x1][y1] += add;
    b[x2 + 1][y1] -= add;
    b[x1][y2 + 1] -= add;
    b[x2 + 1][y2 + 1] += add;

Here we borrow the drawing of [@z deer in the deep forest

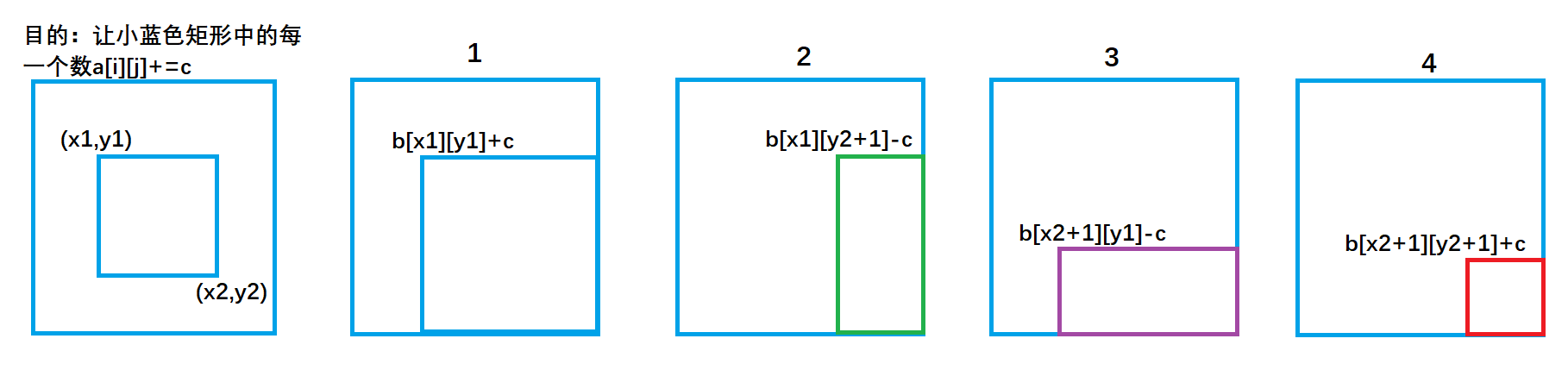
b[x1][ y1 ] +=c; Corresponding to figure 1, C is added to the elements of the blue rectangular area in the whole a array.
b[x1,][y2+1]-=c ; Corresponding to figure 2, subtract C from the elements of the green rectangular area in the whole a array so that the elements in it do not change.
b[x2+1][y1]- =c ; Corresponding to figure 3, subtract C from the elements of the purple rectangular area in the whole a array so that the elements in it do not change.
b[x2+1][y2+1]+=c; Corresponding to figure 4, add C to the elements of the red rectangular area in the whole a array. The elements in red are reduced twice, and then add C once to restore them.

Matrix and calculation

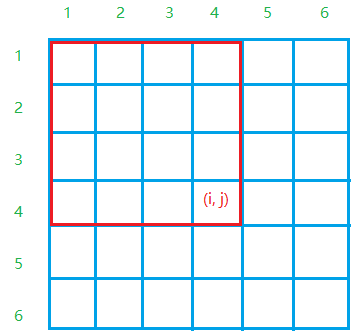
$S[i,j] $is the sum of all numbers in the red box of Figure 1, which is:
$S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]$

The following is the code implementation

//
// Created by Owwkmidream on 2021/10/30.
//
#include "iostream"

using namespace std;

const int N = 1010;

int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int add)
{
    b[x1][y1] += add;
    b[x2 + 1][y1] -= add;
    b[x1][y2 + 1] -= add;
    b[x2 + 1][y2 + 1] += add;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n,m,q;
    cin >> n >> m >> q;

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            int tmp;
            cin >> tmp;
            insert(i ,j, i, j, tmp);
        }
    }

    int x1, x2, y1, y2, c;
    while (q -- ) {
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            a[i][j] = a[i][j-1] + a[i-1][j] - a[i-1][j-1] + b[i][j];
            cout << a[i][j] << " ";
        }
        cout << "\n";
    }

    return 0;
}