Convert binary search tree into cumulative tree
Give the root node of the binary search tree. The node values of the tree are different. Please convert it into a Greater Sum Tree so that the new value of each node is equal to or greater than the node in the original tree Sum of Val values.
Solution:
The characteristic of binary search tree is left < root < right. Now the problem requires that the value of each node is greater than or equal to the value in the original tree.
According to the nature of binary tree, we can traverse the right, root and left order, and add the value of the previous node to the current corresponding node
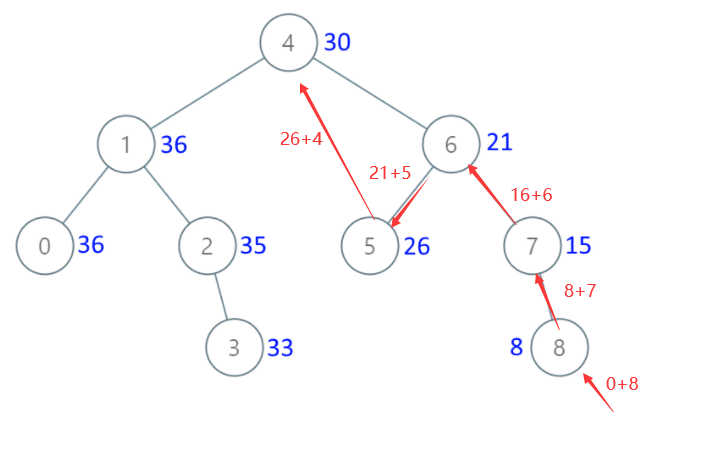
class Solution {
public:
void _convertBST(TreeNode* root,int &prev)
{
if(root==nullptr)
return;
_convertBST(root->right,prev);
root->val+=prev;
prev=root->val;
_convertBST(root->left,prev);
}
TreeNode* convertBST(TreeNode* root) {
int prev=0;
_convertBST(root,prev);
return root;
}
};
House raiding II
You are a professional thief. You plan to steal houses along the street. There is a certain amount of cash in each room. All the houses in this place are in a circle, which means that the first house and the last house are next to each other. If two adjacent houses are equipped with an automatic burglar alarm system, they will be connected to each other at the same time at night.
Given a non negative integer array representing the amount stored in each house, calculate the maximum amount you can steal tonight without touching the alarm device.
Solution:
1. Three variables are given: first represents the money stolen the next day, second represents the money stolen the previous day, and third represents the money stolen today
2. Obviously, the money stolen today = Fmax (stolen yesterday, not stolen yesterday + stolen today)
3. Because it is a ring queue, that is, the head and tail can never be stolen at the same time. At this time, we can split the ring queue into two queues [0, n-1] and [1,n], calculate the total stolen amount respectively, and then return a larger value
class Solution {
public:
int rob(vector<int>& nums) {
//Since the first cannot coexist, it is split into two separate arrays
// 0~n-1 is an array, 1-n is an array, and then operate in the two arrays respectively to return the maximum value
int first=0;
int second=nums[0];
int third=nums[0];
for(int i=1;i<nums.size()-1;i++)
{
third=fmax(first+nums[i],second);
first=second;
second=third;
}
if(nums.size()==1)
return third;
first=0;
second=nums[1];
int third2=nums[1];
for(int i=2;i<nums.size();i++)
{
third2=fmax(first+nums[i],second);
first=second;
second=third2;
}
return fmax(third,third2);
}
};
Longest common subsequence
Given two strings text1 and text2, returns the length of the longest common subsequence of the two strings. If there is no common subsequence, 0 is returned.
The subsequence of a string refers to such a new string: it is a new string composed of the original string after deleting some characters (or not deleting any characters) without changing the relative order of characters.
For example, "ace" is a subsequence of "abcde", but "aec" is not a subsequence of "abcde".
The common subsequence of two strings is the subsequence shared by the two strings.
Solution:
1. Definition dp[i][j] represents the length of the common subsequence in the first I characters of s1 and the first j characters of s2
2. When s1[i]==s2[j], it means that the string of the current position is matched, then dp[i+1][j+1]=dp[i][j] + 1;
**The meaning of this expression is: * * if the current character matches, then the length of dp[i][j] is the previous length + 1
3. When s [i]= S [J] indicates that the characters in the current position do not match, then dp[i+1][j+1]=fmax(dp[i+1][j],dp[i][j+1]);
**The meaning of this expression is: * * if the current length does not match, the length will be the longest length when s1 is one less character, or s2 is one less character. If the characters added by both sides do not match, the point with one less character will be taken
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int len1=text1.size();
int len2=text2.size();
vector<vector<int>>dp(len1+1,vector<int>(len2+1,0));
//dp[i][j] represents the length of the common subsequence in the first I characters of text1 and the first j characters of text2
for(int i=0;i<len1;i++)
{
for(int j=0;j<len2;j++)
{
if(text1[i]==text2[j])//The current character matches
dp[i+1][j+1]=dp[i][j] + 1;
else//The current character does not match
dp[i+1][j+1]=fmax(dp[i+1][j],dp[i][j+1]);
}
}
return dp[len1][len2];
}
};
Longest increasing subsequence
Give you an integer array nums and find the length of the longest strictly increasing subsequence.
A subsequence is a sequence derived from an array. It deletes (or does not delete) the elements in the array without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].
Solution:
1. Define a dynamic array dp[i], the length of the subsequence at the I position of num
2. Given a two-layer loop, the outer loop determines the final position of dp, and the inner loop indicates that it is currently in the j-th element
When nums [i] > nums [J], it indicates that it is increasing. At this time, dp [i] = Fmax (dp [i], dp [J] + 1) - > check all dp values in front of position i. if there is a large one, you can choose to follow it
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int>dp(nums.size(),1);
int max=1;
for(int i=1;i<nums.size();i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
dp[i]=fmax(dp[i],dp[j]+1);
max=fmax(max,dp[i]);
}
}
return max;
}
};
01 matrix
Given a matrix consisting of 0 and 1, find the distance from each element to the nearest 0. The distance between two adjacent elements is 1.
Solution:
1. The distance from a position to the nearest 0 can be selected from four directions. We use an array to save the state in each grid (the position from 0)
2. Traverse the array twice. For the first time, find the nearest position + 1 in the left grid and the upper grid The second traversal, find the lower grid and the right grid
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
vector<vector<int>>ret(mat.size(),vector<int>(mat[0].size(),INT_MAX-1));
//Use the elements on the left and top to find the current element
for(int i=0;i<mat.size();i++)
{
for(int j=0;j<mat[0].size();j++)
{
if(mat[i][j]==0)
{
ret[i][j]=0;
continue;
}
else if(i==0&&j==0)
continue;
else if(i==0)//At this point, mat[i][j] is definitely not 0
{
ret[i][j]=fmin(ret[i][j],ret[i][j-1]+1);
}
else if(j==0)
{
ret[i][j]=fmin(ret[i][j],ret[i-1][j]+1);
}
else
{
int left=ret[i][j-1];
int up=ret[i-1][j];
ret[i][j]=fmin(ret[i][j],fmin(left+1,up+1));
}
}
}
//Construct with the lower right element
int row=mat.size()-1;
int col=mat[0].size()-1;
for(int i=row;i>=0;i--)
{
for(int j=col;j>=0;j--)
{
if(i==row&&j==col)//Bottom right corner
continue;
if(ret[i][j]==0||ret[i][j]==1)//At present, it is the smallest choice
continue;
if(i==row)
{
ret[i][j]=fmin(ret[i][j],ret[i][j+1]+1);
}
else if(j==col)
{
ret[i][j]=fmin(ret[i][j],ret[i+1][j]+1);
}
else
{
int right=ret[i][j+1];
int down=ret[i+1][j];
ret[i][j]=fmin(ret[i][j],fmin(right+1,down+1));
}
}
}
return ret;
}
};