catalogue
2, Introduction and use of stack and queue
3, deque's brief introduction (understanding)
4, Simulation of stack and queue
1. Simulation Implementation of stack
2. Simulation Implementation of queue
3. Implementation of stack and queue in STL library
5, Introduction and Simulation Implementation of priority queue
1. Introduction and use of priority queue
2. Simulation Implementation of priority queue
1, Container adapter
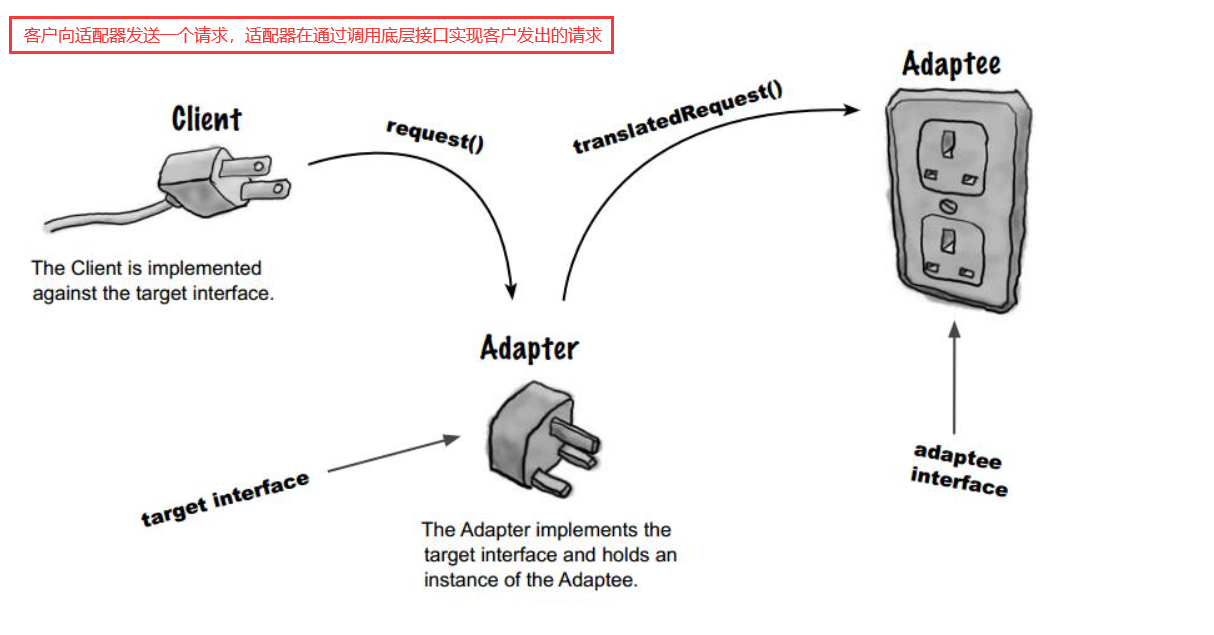
1. What is an adapter?
- Design patterns: design patterns represent best practices and are often adopted by experienced object-oriented software developers. Design pattern is a solution to the general problems faced by software developers in the process of software development. It is a set of code design experience that is repeatedly used, known by most people, classified and catalogued. These solutions are summarized by many software developers after a long period of trial and error.
- Container adapter: an adapter is a design pattern that converts an interface of a class into another interface that the customer wants. It is simply understood that the underlying implementation of one class calls the interface provided by another class.
2, Introduction and use of stack and queue
Stack and queue are Container adapters. Their bottom layer is realized by calling the interfaces of other Container classes. There is a default parameter Container in stack and queue template classes, and the default value is dequeue.

1. Introduction to stack
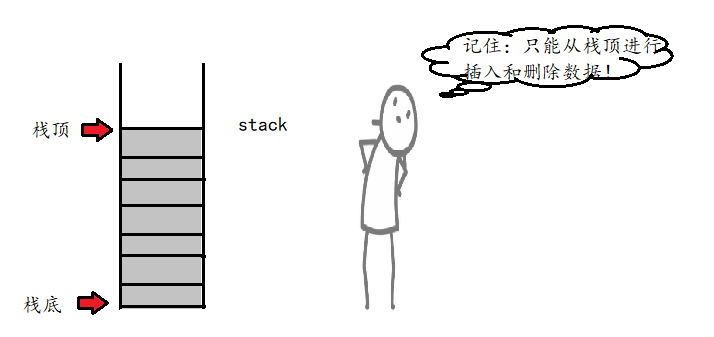
- stack is a container adapter, which is specially used where there is a need for first in and last out operation. stack can only insert and delete data from one end of the container.
- The underlying container of stack can be any standard container class template or some other specific container classes. These classes should support the following operations: empty, back and push_back,pop_back
- The standard vector, deque and list meet these requirements. By default, deque is used if no specific container is specified by stack.
2. Use of stack
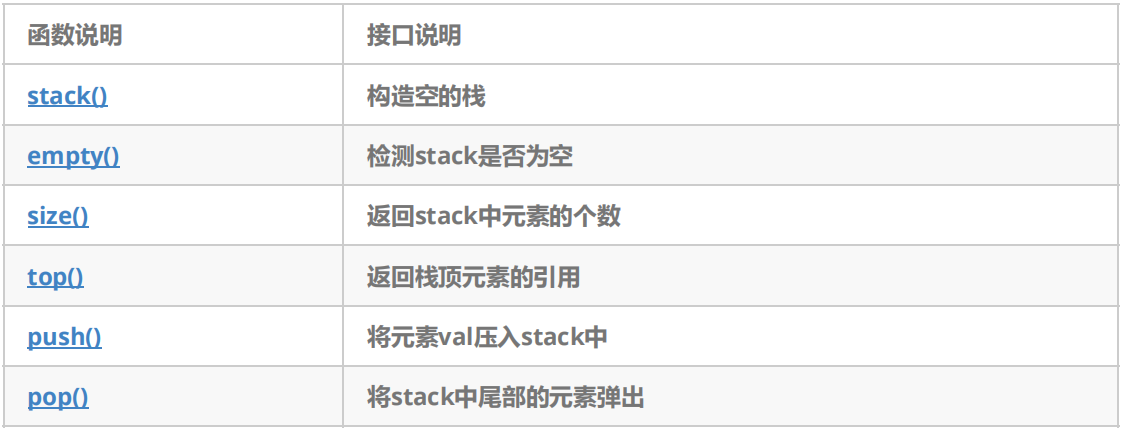
Common interface description of stack
3. Introduction to queue
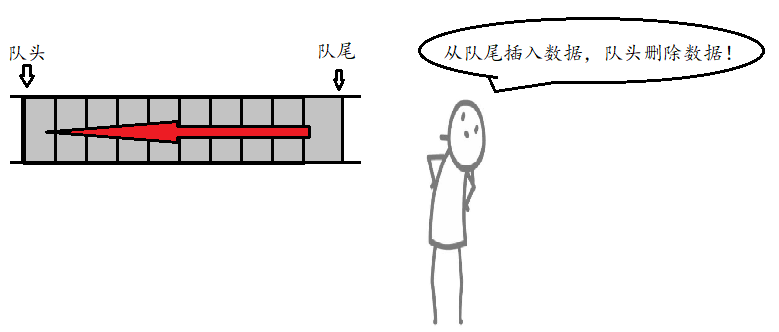
- A queue is a container adapter designed to operate in a "first in first out" context. It can only insert elements from one end of the container and extract elements from the other end.
- The underlying container class can be one of the standard container class templates or other specially designed container classes. These container classes need empty, size, front, back and push_back,pop_front interface
- Queue needs to output data from the queue head, so linear data structures such as vector are not suitable as its underlying container classes, and deque and list can be used as underlying container classes. By default, deque is used if no container class is specified for queue instantiation.
4. Use of queue
3, deque's brief introduction (understanding)
1. Principle of deque
deque (double ended queue): it is a container that can insert and delete data at both ends, and the time complexity is O(1). Compared with vector, it has higher header insertion efficiency, supports random access and high space utilization compared with list.
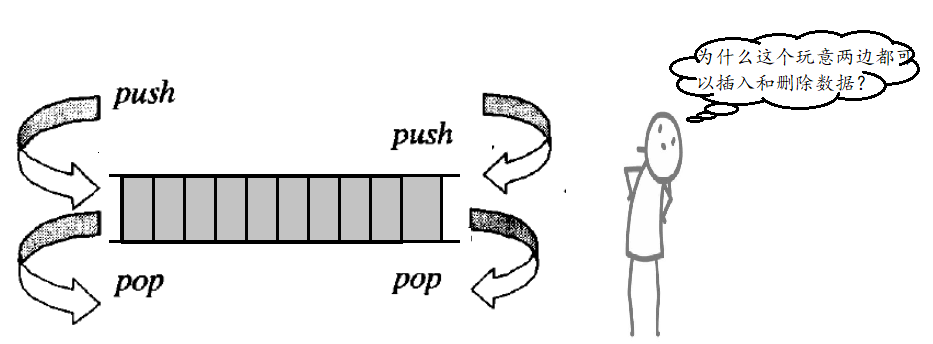
Vector and list are typical representatives of linear structure and chain structure respectively. Vector is characterized by continuous physical space and random access, but it needs to move data when deleting header, with high time complexity; List has discontinuous physical space, can be inserted and deleted randomly, and the insertion and deletion time complexity of head and tail is O(1), but it does not support random access. Deque is a data structure based on vector and list, which can not only support random access, but also the insertion and deletion time complexity on the head is O(1). In that case, why is deque rarely used?
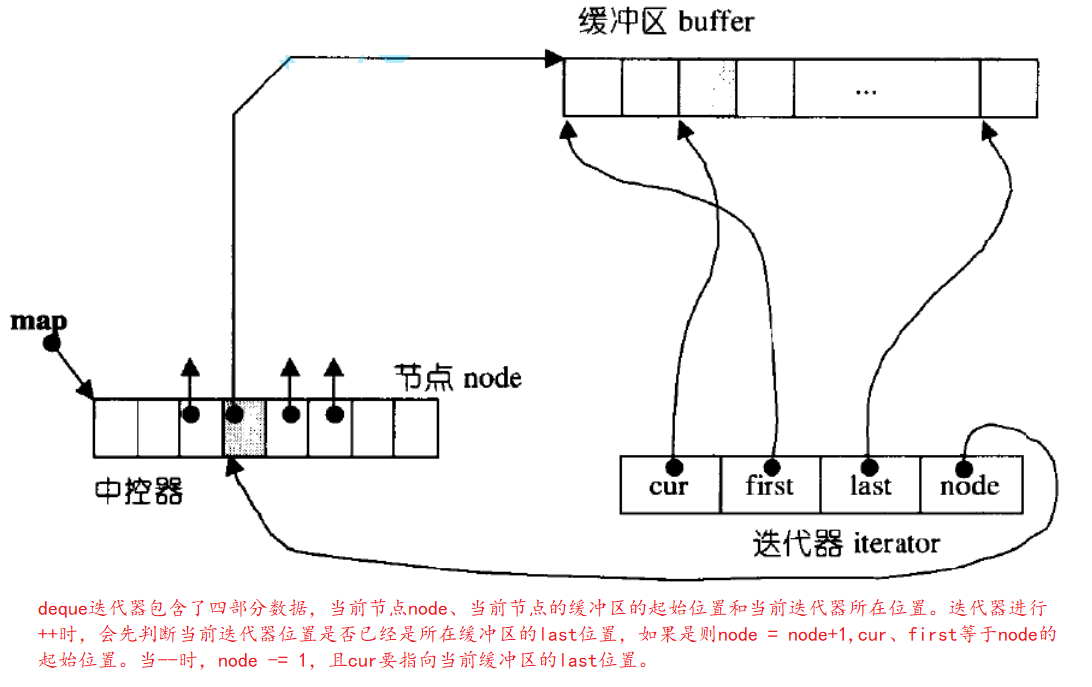
deque is not a real continuous space, but is spliced by sections of space, which is similar to a dynamic two-dimensional array. The underlying structure is as follows:
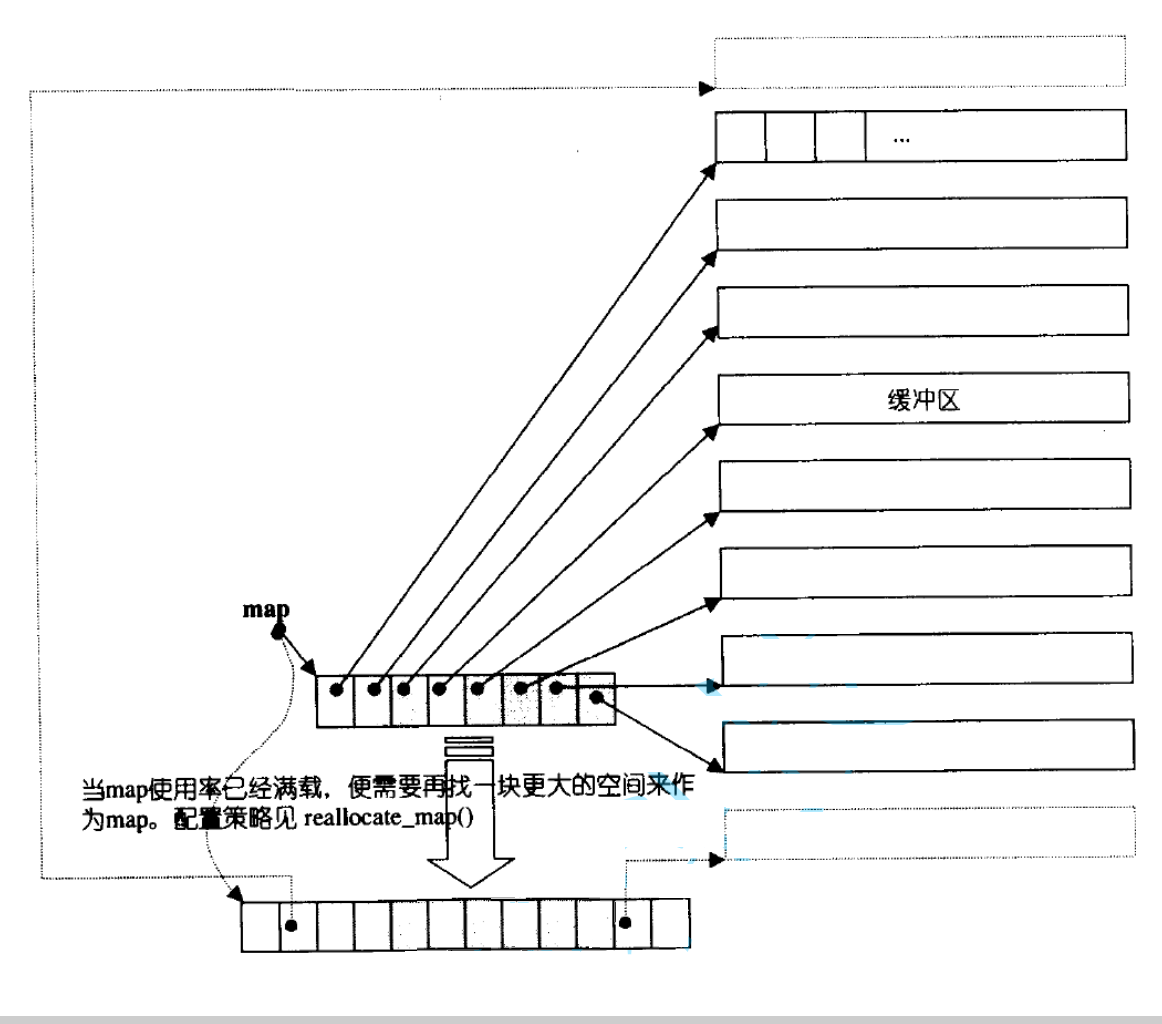
Map is an array pointer that stores the addresses of buffers. When the start map is empty, inserting data into the map will find a buffer to insert from the middle of the map; When inserting data from the front buffer, insert the data from the front buffer; During tail interpolation, insert data from priority to the current buffer. If the current buffer is full, insert data from the next buffer.
The underlying implementation of deque iterator:
2. Defects of deque
- Compared with vector, deque has the advantages of high efficiency of header insertion and deletion, and does not need a large amount of mobile data during capacity expansion (only need to expand the capacity of map).
- Compared with list, deque has the advantages of continuous underlying space, high space utilization and random access.
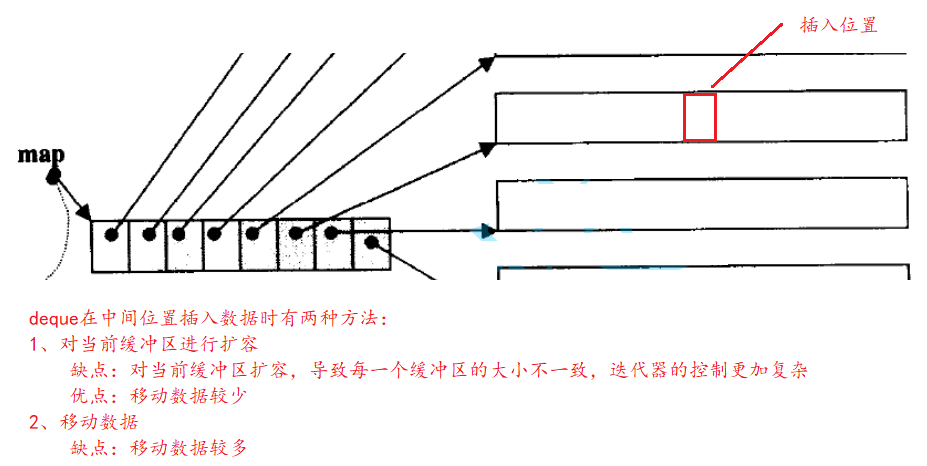
- deque's biggest defect: it is not suitable for traversal - because it needs to frequently detect whether to move to the boundary of a certain buffer space and switch the buffer back and forth, resulting in low efficiency.
- When inserting and deleting data in deque, the efficiency is higher than that of vector and lower than that of list.
4, Simulation of stack and queue
1. Simulation Implementation of stack
namespace bite
{
template<class T>
class stack
{
public:
stack() {}
//Push
void push(const T& x)
{
_c.push_back(x);
}
//Out of stack
void pop()
{
_c.pop_back();
}
//Get stack top element
T& top()
{
return _c.back();
}
const T& top()const
{
return _c.back();
}
//Number of elements in stack
size_t size()const
{
return _c.size();
}
//Judge whether the stack is empty
bool empty()const
{
return _c.empty();
}
private:
std::vector<T> _c;
};
}2. Simulation Implementation of queue
namespace myQueue
{
template<class T>
class queue
{
public:
//The member variables in the queue are all custom types, and the default constructor will call the default constructor of the custom type
queue() {}
//Join the team
void push(const T& x)
{
_c.push_back(x);
}
//Out of the team
void pop()
{
_c.pop_front();
}
//Tail element
T& back()
{
return _c.back();
}
const T& back()const
{
return _c.back();
}
//Team head element
T& front()
{
return _c.front();
}
const T& front()const
{
return _c.front();
}
//Number of elements in the queue
size_t size()const
{
return _c.size();
}
//Judge team empty
bool empty()const
{
return _c.empty();
}
private:
std::list<T> _c;
};
}3. Implementation of stack and queue in STL library
template<class T, class Con = deque<T>>
class stack
{
public:
stack() {}
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_back();
}
T& top()
{
return _c.back();
}
const T& top()const
{
return _c.back();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
Con _c;
};
template<class T, class Con = deque<T>>
class queue
{
public:
queue() {}
void push(const T& x)
{
_c.push_back(x);
}
void pop()
{
_c.pop_front();
}
T& back()
{
return _c.back();
}
const T& back()const
{
return _c.back();
}
T& front()
{
return _c.front();
}
const T& front()const
{
return _c.front();
}
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
private:
Con _c;
};5, Introduction and Simulation Implementation of priority queue
1. Introduction and use of priority queue
- priority_queue is a container adapter. According to the strict weak sorting standard, its first element is always the largest (smallest) of the elements it contains.
- The priority queue is similar to the heap and can only retrieve the top elements of the heap.
-
The underlying container can be any standard container class template or other specially designed container classes. Containers should be accessible through random access iterators and support the following operations: empty, size, push_back,pop_back,front
-
The standard container classes vector and deque meet these requirements. By default, if there is no specific priority_ If the queue class instantiates the specified container class, vector is used.
-
Random access iterators need to be supported in order to always maintain the heap structure internally. The container adapter automatically calls the algorithm function make when needed_ heap,push_heap and pop_heap to do this automatically.
|
Function declaration
|
Interface description
|
|
priority_queue()/priority_queue(fifirst,
last)
|
Construct an empty priority queue
|
|
empty( )
|
Check whether the priority queue is empty and return yes
true
, otherwise return
false
|
|
top( )
| Returns the largest (smallest) element in the priority queue, that is, the top element of the heap |
|
push(x)
| Insert element in priority queue |
|
pop
()
|
Delete the highest priority in the queue
(
minimum
)
Element, i.e. top of heap element
|
Note: by defau lt, the priority queue is large; If you use priority queues to store custom types, you need to provide overloads of > and <
2. Simulation Implementation of priority queue
In the priority queue, when inserting a data, you need to ensure that it is still a heap after insertion. Therefore, you need to use the up adjustment algorithm to adjust the heap during insertion; When deleting a data from the priority queue, it is necessary to exchange the top of the heap with the last element of the heap, and delete the last element before adjusting the heap.
namespace myPriorityQueue
{
//functor
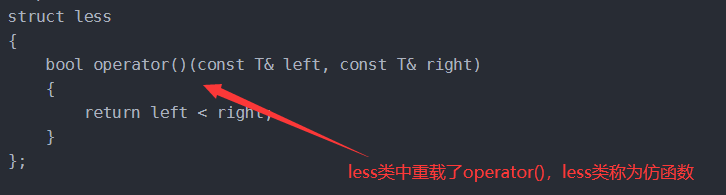
template<class T>
struct less
{
bool operator()(const T& left, const T& right)
{
return left < right;
}
};
template<class T>
struct greater
{
bool operator()(const T& left, const T& right)
{
return left > right;
}
};
template<class T,class container = vector<T>,class compare = greater<T>>
class priority_queue
{
public:
//Default constructor - it seems that every time you write anything, you actually call the default constructor of the custom type for the custom type constructor
priority_queue(){}
template<class Iterator>
priority_queue(Iterator first, Iterator last)
: _con(first, last)
{
int root;
// Will_ The elements in con adjust the structure of the heap
//Method 1 --- use the up adjustment algorithm from top to bottom
for (root = 0; root < _con.size(); root++)
AdjustUP(root);
//Method 2 --- use the downward adjustment algorithm from bottom to top
/*for (root = (_con.size() - 2) / 2; root >= 0; root--)
AdjustDown(root);*/
}
//Insert element
void push(const T& data)
{
//The priority queue is similar to the heap. When inserting data, you need to use the upward adjustment algorithm to adjust it into the heap
_con.push_back(data);
AdjustUP(_con.size() - 1);
}
//Delete element
void pop()
{
//When deleting elements from the heap, exchange the first and last elements, delete the last element, and use the downward adjustment algorithm in the heap array to adjust it into a heap
if (empty())
return;
swap(_con.front(), _con.back());
_con.pop_back();
AdjustDown(0);
}
//Number of elements
size_t size()const
{
return _con.size();
}
//Air judgment
bool empty()const
{
return _con.empty();
}
// The heap top element is not allowed to be modified because: the modification of the heap top element can destroy the characteristics of the heap
const T& top()const
{
return _con.front();
}
void test()
{
for (auto e : _con)
cout << e << " ";
cout << endl;
}
private:
//Downward adjustment algorithm
void AdjustDown(int root)
{
int child = root * 2 + 1;
while (child < _con.size())
{
// Find older children with parent as root
if (child + 1 < _con.size() && compare()(_con[child+1],_con[child]))
child += 1;
// Check whether the parents meet the requirements
if (compare()(_con[child], _con[root]))
{
swap(_con[child], _con[root]);
root = child;
child = root * 2 + 1;
}
else
break;
}
}
//Upward adjustment algorithm
void AdjustUP(int child)
{
//Parent child node comparison. If the child node is larger than the parent node, it will be exchanged
int parent = (child - 1) / 2;
while (child > 0)
{
if (compare()(_con[child], _con[parent]))
{
swap(_con[child], _con[parent]);
//Continue iteration down
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
private:
container _con;
};
}In priority_ In the simulation implementation of queue, there are two classes: less and greater to control whether to create a large heap or a small heap. These two classes are called imitation functions.
6, Imitative function
An imitation function is a class that overloads the () operator and can be called like a function. In C language, we can use function pointers to solve priority_ The problem of creating a large heap or a small heap in queue can be solved by using imitation functions in C + +.