Title Description

Obviously, four strides can be used to climb n steps. Of course, the physical strength of each stride is also different. The corresponding relationship is as follows

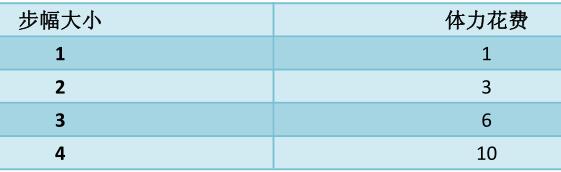
Mingming began to have m physical strength. How many steps should he take to finish all the steps?

1 1

2 3

3 6

4 10

input

There are only two positive integers, N and m, with a space in the middle as the spacer. 0<n<=m.
For 30% of the data, m < 100
For 60% of the data, m < 10000
For 80% of the data, m < 1000000
For data of 100, m < 10 ^ 19

output

An integer indicating the minimum number of steps to complete all steps?

sample input  

3 5

sample output  

2

Idea:

It is easy to analyze the law 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4 by looking at the table

Look at the data range and find that 10 ^ 19 consider writing an answer with a time complexity of O(1)

If n = 5 and M = 5, then it is 1 (each step consumes a total of 5 physical strength)

If m becomes 6, then it is 1 2  

It is not difficult to find that the number pair {1, 1} - > {2} requires 1 more physical strength

Similarly, {1, 2} - > {3} requires 2 more points of physical strength. All compression methods can be introduced. The more the number of compressed objects, the more physical strength it takes

In other words, the higher the cost, under this idea, it is not difficult to find that the best answer is to turn all 1 into 2 until it can not be changed, and then turn 2 into 3

Since you need the answer of O(1), you can write the number and judge directly~

    ll T1= n;
    ll T2= (n - (n % 2)) * 3 / 2 + n % 2;
    ll T3= (n - (n % 3)) * 2 + n % 3;
    ll T4= (n - (n % 4)) * 5 / 2 + n % 4;

T2 is the physical strength required to turn all walking methods into 2. Finally, add n% 2 to be the remaining "1"

T3 and T4 are the same, but the remaining number in the state is still "1", so special judgment is required in the code

For example, if n% 3 = 1, there will be 1 left at last. When compressing later, priority should be given to compressing {1, 3} - > {4}  

Then compress {3, 3, 3} - > {4, 4, 4} (that is, the transfer between the two factors of lcm)  

Solution:

/*
************************************
***********emu^w^***********
 
*/

#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
const int P = 13131;
#define ll long long
const int mod = 1E6 + 7;
const int INF = 0x3f, sINF = 0x3f3f3f3f;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<long long, long long> PLL;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
//
const int N = 500010;
ll n, m;

int main()
{
    cin>>n>>m;

    ll T1= n;
    ll temp = m;
    ll T2= (n - (n % 2)) * 3 / 2 + n % 2;
    ll T3= (n - (n % 3)) * 2 + n % 3;
    ll T4= (n - (n % 4)) * 5 / 2 + n % 4;
//    cout<<T1<<endl;    cout<<T2<<endl;    cout<<T3<<endl;    cout<<T4<<endl;
    
    if(m >= T1 && m < T2) {
        temp -= n;
        cout<<n - temp<<endl;
    }  
    else if(m >= T2 && m < T3)
    {
        temp -= T2;
        ll ans = n / 2 + n % 2;
        if(n % 2) if(temp >= 2) {
            temp -= 2;
            ans--;
        }
        if(temp >= 3) ans -= temp / 3;
        cout<<ans<<endl;
    }
    else if(m >= T3 && m < T4) {
        temp -= T3;
        ll ans = n / 3 + n % 3;
        if(n % 3 == 2) {
            temp--;
            ans--;
        }
        if(n % 3 == 1 && temp >= 3)  {
            temp -= 3;
            ans--;
        }
        if(n % 3 == 2 && temp >= 5) {
            temp -= 5;
            ans--;
        }
        if(temp >= 6) ans -= temp / 6;
        
        cout<<ans<<endl;
    }
    else {
        ll ans = n / 4 + n % 4;
        temp -= T4;
        if(n % 4 == 2 && temp >= 1) {
            temp--;
            ans--;
        } 
        if(n % 4 == 3 && temp >= 1) {
            temp--;
            ans--;
        }
        if(n % 4 == 3 && temp >= 2) 
        {
            temp -= 2;
            ans--;
        }
        cout<<ans<<endl;
    }


}

Time complexity: O(1);

Type: conditional judgment