1, Foreword

  in the past, the sorting methods we studied were based on comparison, and their efficiency was either quadratic or logarithmic. Bucket sorting is based on container sorting, which is mainly divided into count sorting and cardinality sorting. This paper describes the knowledge of cardinality sorting.
  the idea of cardinality sorting is divided into two parts: distribution and collection.

2, Distribution and collection graphic analysis

Distribution idea:
   use the highest priority or the lowest priority (number, ten, hundred, thousand, ten thousand...), traverse the array according to a keyword value, and divide the data into the corresponding bucket.
   here, the data is allocated to ten buckets of 0 ~ 9, because the range of a bit of any data is in the range of 0 ~ 9.
Collect ideas:
  put the values allocated to the bucket back into the array in turn. According to the first in, first out (first in, first out) of the first in bucket.

Distribution and collection diagram:
   there is a group of data as follows, which are sorted in ascending order by cardinality sorting:

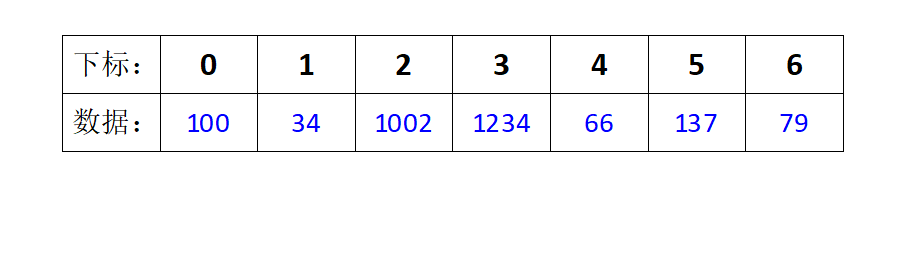
First distribution and collection:

  at this time, the single bit of the data is sorted from small to large.

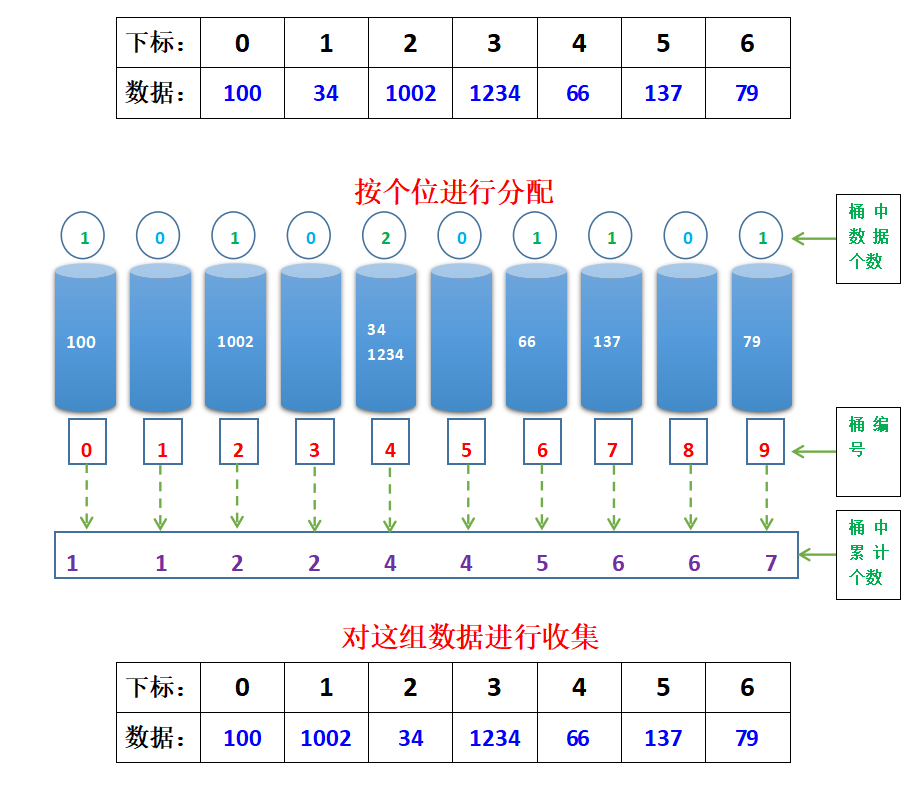
Second distribution and collection:

  now the ten digits of the data are sorted from small to large.

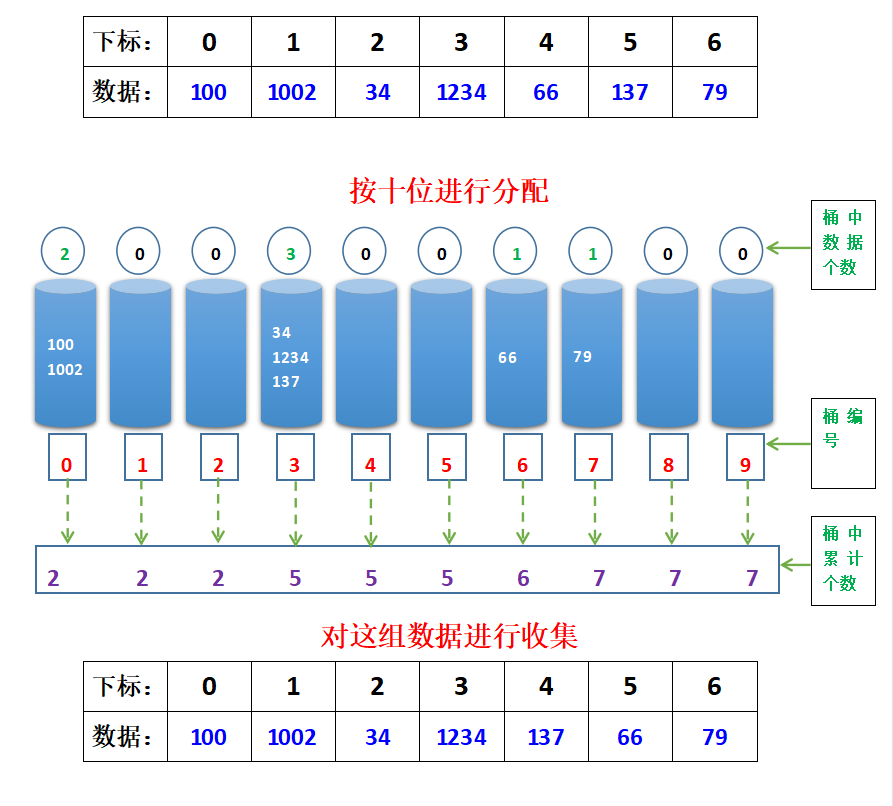
Third distribution and collection:

  the hundred digits of the same data are sorted from small to large.
Fourth distribution and collection:

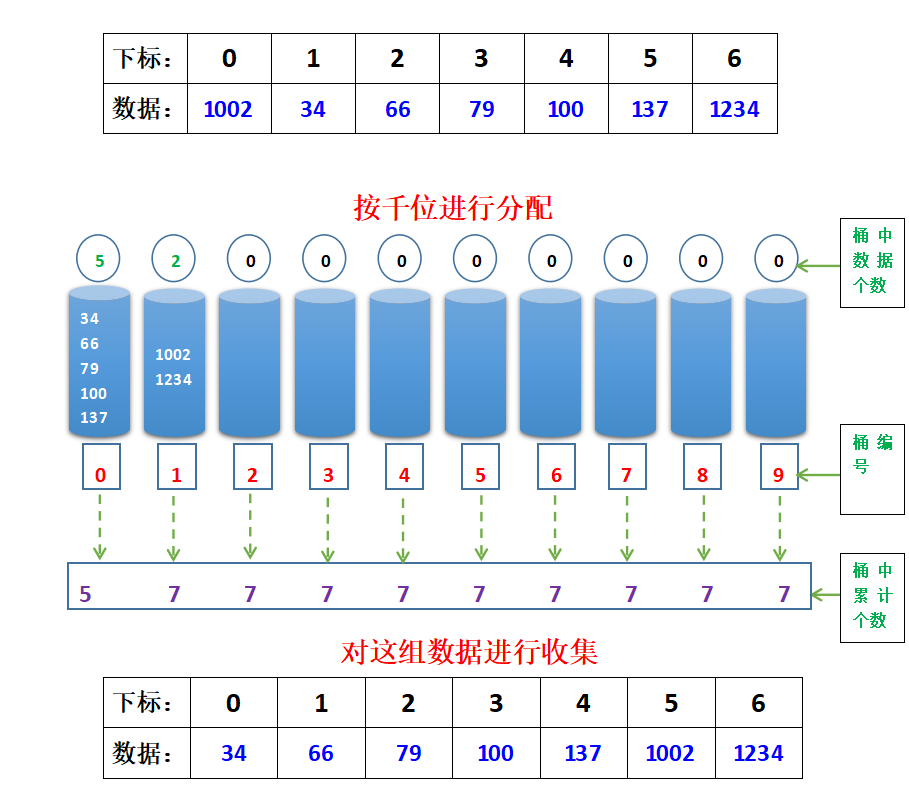
  when the distribution and collection by thousands are completed, the data will become orderly and the sorting will be completed.

3, Difficulties of cardinality sorting algorithm

   the idea of cardinality sorting is easy to understand. However, the implementation of the code does not really put the data into the bucket as we described. It uses the idea of bucket to count the number of data in each bucket, and then accumulate the number of data in the bucket. Through the final accumulation result, it is concluded that the data in the original array will be copied to the auxiliary array The location of the array to complete the collection.
  that is to say, the real function of the bucket is to calculate the location, not to store data.
  therefore, our bucket will be a one-dimensional array with a capacity of 10, initialized to zero. Through a series of calculations, we can get where the original array data will be copied to the auxiliary array.

4, Design of Radix sorting algorithm

   combined with the above analysis, an allocation process in the algorithm is given, which should be in the following state

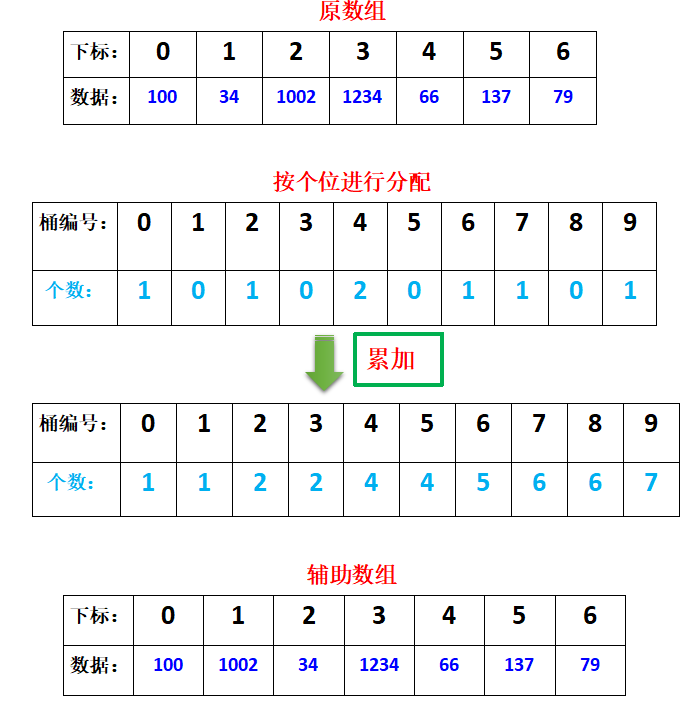
   we copy the data in the original array to the auxiliary array with the help of the records in the bucket. How to calculate the position? Traverse the array subscripts in descending order. According to the number of data retrieval buckets, the number of records in the bucket minus 1 is the position of the data in the auxiliary array. When a data is collected, the number of records in the bucket should be reduced by one.
   for example, in the above example, first traverse the position with the subscript of 6 in the original array, the position data is 79, the corresponding bucket number is bucket 9 by bit, and the record in bucket 9 is 7, then the position of the data in the auxiliary array is 7-1 = position 6. After we determine the position of a data, we need to subtract 1 from the record in the bucket. Therefore, the records in bucket 9 become 6. In turn Array subscript 5

  what determines the allocation times? The allocation times are determined by the maximum number of data in the group.

The cardinality sorting algorithm should include these parts:
  · calculate the maximum value in this set of data to determine the allocation times;
  · calculate the number of data stored in each bucket;
  · update the data in the bucket to the cumulative number;
  · determine which position in the auxiliary array the data will be collected according to the records in the bucket;
  · copy the data in the auxiliary array back to the original array.

5, Implementation of Radix sorting algorithm

  based on the above analysis, let's implement the cardinality sorting algorithm.

void radixSort(int array[], int size)
{
	int max = array[0];//The maximum value used to mark this set of data
	int base = 1;//Marked divisor
	int* tempAry = (int*)malloc(sizeof(int) * size);//Auxiliary array for temporary storage of data
	if (!tempAry)exit(-1);//Failed to open space, return - 1
	for (int i = 1; i < size; i++)//Traverse to find the maximum value of this set of data
	{
		if (array[i] > max)
		{
			max = array[i];
		}
	}
	while (max / base > 0)//Allocate and collect, and the allocation times are determined by the maximum data
	{
		int bucket[10] = { 0 };//Apply for initialization of 10 buckets to zero for recording the number
		int number;//Number used to mark the bucket
		int pos;//Used to mark the position of the auxiliary array
		for (int i = 0; i < size; i++)//Count the number of data in each bucket
		{
			number = array[i] / base % 10;//Calculate the bucket number
			bucket[number]++;//The number of data in the bucket is increased by one
		}
		for (int i = 1; i < 10; i++)//Cumulative update of records in bucket
		{
			bucket[i] += bucket[i - 1];
		}
		for (int i = size - 1; i >= 0;i--)//Copies data to the auxiliary array in reverse order
		{
			number = array[i] / base % 10;//Calculate bucket number
			pos = bucket[number] - 1;//Calculate where you need to copy to the auxiliary array
			tempAry[pos] = array[i];//Copy
			bucket[number]--;//Number of records minus one
		}
		for (int i = 0; i < size; i++)//Copying data to the original array
		{
			array[i] = tempAry[i];
		}
		base *= 10;//For each distribution and collection, the divisor is expanded by 10 times
	}
	free(tempAry);//Release temporary array
}

Test main function:

int main()
{
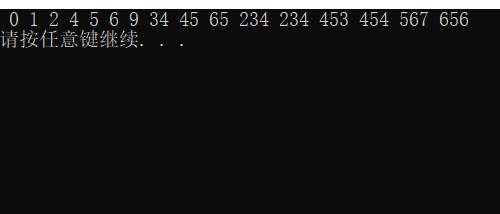
	int array[]{ 234,453,454,234,656,6,567,65,9,34,4,45,2,5,0,1 };
	int size = sizeof(array) / sizeof(int);
	radixSort(array, size);
	for (int i = 0; i < size; i++)
	{
		std::cout << " " << array[i];
	}
	std::cout << char(10);
	system("pause");
	return 0;
}

Test results:

6, Summary

   the time complexity of Radix sorting is O(N), and the space complexity is O(N). It is a stable sorting. However, its application range is limited, and the data status of samples needs to meet the division of buckets.
  I hope it will be helpful to you.

  I'm Lao Hu, thank you for reading!! ❤️ ❤️