Solution CF903G Yet Another Maxflow Problem

Title Link

Topic description

Given a graph, there are \ (n \) nodes on the left and right, \ (A_i\to A_{i+1} \) edges, \ (B_i\to B_{i+1} \) edges, and the capacity is given.
There is an edge between \ (m \) and \ (A_i\to B_j \), and the capacity is given.
You need to find the maximum flow of the original graph from \ (A_1 \) to \ (B_n \), and then there are \ (q \) operations. Each operation gives \ (I \), first modify the capacity of the edge of \ (a_i \ to a {I + 1} \), and then ask for the maximum flow from \ (A_1 \) to \ (B_n \).

Solution:

Obviously, if the maximum flow turns to the minimum cut first, which edges to cut is the best.

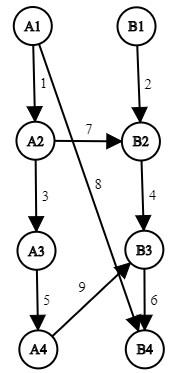
It can be found that there are four choices for edge cutting: cut or not on the left chain, cut or not on the right chain. Four choices are obtained by multiplication principle.

We don't want too much classification discussion, so we can add an edge above \ (A_1 \) to represent the left non cutting edge, and add an edge below \ (B_n \) to represent the right non cutting edge. Then the problem is to cut some edges on the left and some edges on the right, and then cut off the edge connected with \ (A_1,B_n \) in the middle to find the minimum cost of all schemes.

Cutting multiple edges at the same time on the left or right is obviously not optimal, because only the broken edge closest to \ (A_1,B_n \) produces the cutting effect, so the problem can be abstracted into a formula:

Now return to the topic: \ (q \) operations. Each operation gives \ (I \), first modify the capacity of the side of \ (a_i \ to a {I + 1} \), and then ask for the maximum flow from \ (A_1 \) to \ (B_n \).

Note that the modification is only made on the left, so for cutting off a left edge \ (A_x\to A_{x+1} \), the corresponding

Is constant. Consider using the segment tree, put \ (B \) on the segment tree, add \ (A_x \) from \ (1 \) to \ (n \), enumerate the edge set \ (E(x,v) \) of each new point, add the interval corresponding to the interval \ (v\sim n \) on the segment tree, and then find the global minimum. After the request, the

Put a new line segment tree into it. The subsequent operation is to modify the \ (\) global minimum value at a single point and maintain it directly.

code:

#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
#define N 200005
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
#define il inline
#define file(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
il int read(){
	int w=0,h=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')h=-h;ch=getchar();}
	while(ch>='0'&&ch<='9'){w=w*10+ch-'0';ch=getchar();}
	return w*h;
}
struct Edge{
	int next,to,val;
}edge[N];
int n,m,q;
int head[N],num;
int A[N],B[N],res[N];
void add(int u,int v,int w){
	edge[++num].next=head[u];
	edge[num].to=v;
	edge[num].val=w;
	head[u]=num;
}
namespace SGT{
	int Min[N<<2],Tag[N<<2];
	void pushup(int k){Min[k]=min(Min[ls],Min[rs]);}
	void pushdown(int k){
		if(!Tag[k])return;
		Min[ls]+=Tag[k];Min[rs]+=Tag[k];
		Tag[ls]+=Tag[k];Tag[rs]+=Tag[k];
		Tag[k]=0;
	}
	void build(int k,int l,int r){
		Tag[k]=0;
		if(l==r){
			Min[k]=B[l];
			return;
		}
		build(ls,l,mid);
		build(rs,mid+1,r);
		pushup(k);
	}
	void modify(int k,int l,int r,int x,int y,int val){
		if(l>=x&&r<=y){
			Min[k]+=val;
			Tag[k]+=val;
			return;
		}
		pushdown(k);
		if(x<=mid)modify(ls,l,mid,x,y,val);
		if(mid<y)modify(rs,mid+1,r,x,y,val);
		pushup(k);
	}
}
signed main(){
	n=read();m=read();q=read();
	for(int i=2;i<=n;i++)A[i-1]=read(),B[i]=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		add(u,v,w);
	}
	SGT::build(1,1,n);
	for(int i=1;i<=n;i++){
		for(int j=head[i];j;j=edge[j].next){
			int v=edge[j].to,w=edge[j].val;
			SGT::modify(1,1,n,1,v,w);
		}
		res[i]=SGT::Min[1];
	}
	for(int i=1;i<=n;i++)B[i]=res[i]+A[i];
	SGT::build(1,1,n);
	printf("%lld\n",SGT::Min[1]);
	while(q--){
		int x=read(),val=read();
		SGT::modify(1,1,n,x,x,val-A[x]);
		A[x]=val;
		printf("%lld\n",SGT::Min[1]);
	}
	return 0;
}